什么是范数【向量范数、矩阵范数】

---

一、定义

范数，在线性代数、泛函分析及相关的数学领域，是一个函数，其为向量空间内的所有向量赋予非零的正长度或大小。范数事实上就是线性空间上定义的一类函数，这类函数需要满足三条性质，具体定义如下：

设$\mathcal{X}$是给定的线性空间，向量范数 $\Vert ?\Vert$ 是定义在$\mathcal{X}$上的实值函数, 对 $\mathcal{X}$中的任意向量 $\vec{x}$ 和 $\vec{y}$, 满足:

1. $\Vert \vec{x}\Vert \ge 0$ ，当且仅当 $\vec{x}=0$ 时， $\Vert \vec{x}\Vert =0$ （正定性）
2. $\Vert k\vec{x}\Vert =\mid k\Vert \vec{x}\Vert ,k$ 是任一实数 (齐次性)
3. $\Vert \vec{x}+\vec{y}\Vert \le \Vert \vec{x}\Vert +\Vert \vec{y}\Vert$ (三角不等式)

二、向量范数

由向量范数的定义，我们可以给出向量${?}_p$-范数的定义：
定义(${?}_p$-范数)

若向量$\mathrm{x}=[x_1,x_2,?,x_n{]}^T$,则其${?}_p$-范数为：
$$\begin{array}{c}\Vert \mathrm{x}{\Vert }_p=(\sum _{i=1}^n{x}_i^p{)}^{\frac{1}{p}}\end{array}\text{\hspace{1em}?}$$

（1）L0范数

根据p的取值的变化，可以得到不同的范数， 当 $p=0$, 我们就有了 $l_0$-范数, 即：
$$\begin{array}{c}\Vert \mathbf{x}{\Vert }_0=\sqrt[0]{\sum _i{x}_i^0}\end{array}\text{\hspace{1em}?}$$
表示向量 $\mathbf{x}$ 中非0元素的个数 。在诸多机器学习模型中,比如多任务学习中的行稀疏问题 , 我们很多时候希望最小化向量的 ${?}_0$-范数。然而, 由于 ${?}_0$-范数仅仅表示向量中非0元素的个数, , 这个优化模型在数学上被认为是一个 NP-hard问题，即直接求解它很复杂。正是由于该类优化问题难以求解, 因此,很多时候是将 ${?}_0$-范数最小化问题，转换成 ${?}_1$-范数最小化问题。

（2）L1范数

当p=1时，可以得到常见的${?}_1$-范数，${?}_1$-范数有很多的名字, 例如我们熟悉的曼哈顿距离、最小绝对误差等。它的定义如下:
$$\begin{array}{c}\Vert \mathbf{x}{\Vert }_1=\sum _{i=1}^n\left|x_i\right|\end{array}\text{\hspace{1em}?}$$${?}_1$-范数表示向量x中非零元素的绝对值之和。对于${?}_1$-范数, 它的优化问题为：
$$\min \Vert \mathbf{x}{\Vert }_1={\Sigma }_{i=1}^n|x_i|$$由于${?}_1$-范数的性质, 对其优化的解是一个稀疏解, 因此 ${?}_1$-范数也被叫做稀疏规则算子。

1. 在经典的线性回归问题中运用${?}_1$-范数，也被称为Lasso回归。Lasso回归通过${?}_1$-范数可以实现特征的稀疏或者说特征选择，${?}_1$-范数会将一些特征的权重压缩到 0，从而实现自动的特征筛选和降维的效果。
2. 通过${?}_1$-范数的特征选择还可以避免模型的过拟合问题，原因在于它能够减少模型的复杂度，并去除那些对目标变量没有贡献或贡献较小的特征，这样做可以提高模型的泛化能力，从而降低过拟合的风险。

（3）L2范数

当p=2时，可以得到${?}_2$-范数，${?}_2$-范数是我们最常见最常用的范数了, 我们用的最多的度量距离欧氏距离就是一种${?}_2$-范数, 它的定义如下：
$$\begin{array}{c}\Vert \mathbf{x}{\Vert }_2=\sqrt{\sum _{i=1}^n{x}_i^2}\end{array}\text{\hspace{1em}?}$$
表示向量元素的平方和再开平方。

1. 同${?}_1$-范数一样，${?}_2$-范数也常会被用来做优化目标函数的正则化项，${?}_2$-范数正则化会对模型参数的平方和进行惩罚，使得模型的权重趋向于分布在较小的范围内，这样做可以有效避免过于复杂的模型，从而提升模型的泛化能力。
2. 在经典的线性回归问题中，加入${?}_2$-范数的约束，被称为岭回归，可参考文章。

（4）等价范数

这里总结一下常用的向量范数：

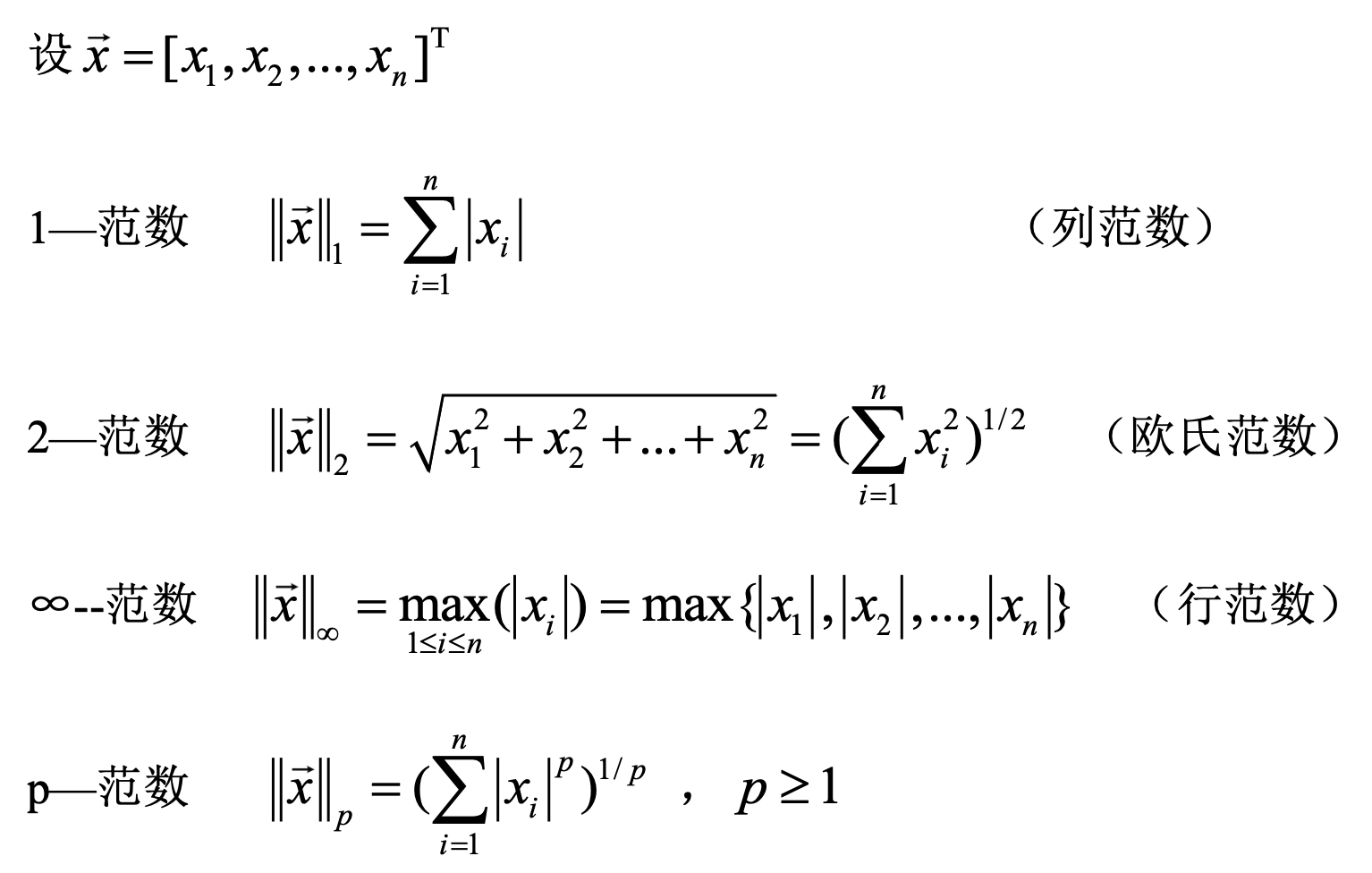
事实上, 线性空间$\mathcal{X}$ 中任意两种范数都是等价的

如果 $\mathcal{X}$ 中有两个范数 $\Vert ?\Vert$ 和 $\Vert ?\Vert \prime$, 存在实数 $m,M>0$, 使得对任意 $n$ 维向量 $\mathbf{x}$, 都有 :
$$m\Vert x\Vert ?\Vert x{\Vert }^{\prime }?M\Vert x\Vert$$
则称这两种范数是等价的。

• 对于两种等价的范数，同一向量序列有相同的极限.

下面以无穷范数和二范数为例，证明它们的等价性：

由无穷范数的定义可得： ∥ x ∥ ∞ = max ? 1 ? i ? n { ∣ ∣ x i ∣ ∣ } ? x 1 2 + x 2 2 + ? + x n 2 = ∥ x ∥ 2 \|\boldsymbol{x}\|_{\infty}=\max _{1 \leqslant i \leqslant n} \left\{|| x_i ||\right\} \leqslant \sqrt{x_1^2+x_2^2+\cdots+x_n^2}=\|\boldsymbol{x}\|_2 ∥x∥∞?=1?i?nmax?{∣∣xi?∣∣}?x12?+x22?+?+xn2? ?=∥x∥2?
设 ∥ x ∥ ∞ = ∣ x j ∣ = max ? 1 ≤ i ≤ n { ∣ x i ∣ } \|\boldsymbol{x}\|_{\infty}=\left|x_j\right|=\max\limits_{1\leq i\leq n}\left\{\left|x_i\right|\right\} ∥x∥∞?=∣xj?∣=1≤i≤nmax?{∣xi?∣}, 则:
$$\Vert \mathbf{x}{\Vert }_{\infty }=\left|x_j\right|?\sqrt{\frac{x_1^2+x_2^2+?+x_n^2}{n}}=\frac{\Vert \mathbf{x}{\Vert }_2}{\sqrt{n}}$$
所以, 2- 范数与 $\infty ?$ 范数是等价的

二、矩阵范数

矩阵范数有较多的定义，这里介绍几种常见的矩阵范数定义。

（1）Element-wise Norm

类似向量$l_p$范数的定义，Element-wise矩阵范数定义如下：

对$A\in {\mathbb{R}}^{n\times m}$,其$l_p$范数为：
$$\Vert A{\Vert }_p={\left(\sum _{i=1}^n\sum _{i=1}^m{\left|a_{ij}\right|}^p\right)}^{\frac{1}{p}}$$

事实上，这个也可以看作向量范数的一种，我们将矩阵向量化：
$$\mathrm{Vec}(A)={\left[\begin{array}{c}{A}_1\\ A_2\\ ?\\ A_m\end{array}\right]}_{mn}?\Vert A{\Vert }_p=\Vert \mathrm{vec}(A)\Vert p$$
一个常用的矩阵范数是$p=2$时，也就是Frobenius范数：
$$\Vert A{\Vert }_2={\left(\sum _{i=1}^m\sum _{i=1}^n{\left|a_{ij}\right|}^2\right)}^{\frac{1}{2}}$$
也常记为$\Vert ?{\Vert }_F$：
$$\Vert A{\Vert }_F=\sqrt{\mathrm{tr}\left(A^{T}A\right)}=\sqrt{\sum {\sigma }_i^2(A)}$$
第一个等号由迹运算定义可以得到，第二个等号证明如下：

证明：

设矩阵$A$奇异值分解为$A=U\Sigma V^T$，结合$\Vert ?{\Vert }_F$是酉不变范数(见第五小节的介绍)可得：
$$\Vert A{\Vert }_F=\Vert U\Sigma V^T{\Vert }_F=\Vert \Sigma {\Vert }_F=\sqrt{\sum _{i=1}^n{\sigma }_i^2}.$$

（2）Induced Norm

矩阵$A\in {\mathbb{R}}^{n\times m}$的诱导范数也被称为算子范数(operator norm)，定义如下：

对任意$A\in {\mathbb{R}}^{n\times m}$，其诱导p范数为：
$$\begin{gathered} \Vert A{\Vert }_p=\underset{x\in {\mathbb{R}}^m,x\ne 0}{\sup }\frac{\Vert Ax\Vert p}{\Vert x{\Vert }_p} \\ =\underset{\begin{array}{c}x\in {\mathbb{R}}^m\\ \Vert x{\Vert }_p=1\end{array}}{\sup }\Vert Ax{\Vert }_p. \end{gathered}$$

常见的诱导矩阵范数如下：
$$\begin{array}{rl}& \Vert A{\Vert }_1=\underset{1\le j\le m}{\max }\sum _{i=1}^n\left|a_{ij}\right|(最大列和)\\ & \Vert A{\Vert }_2={\sigma }_1(A)(\text{?谱范数?}).\\ & \Vert A{\Vert }_{\infty }=\underset{1\le i\le n}{\max }\sum _{j=1}^m\left|a_{ij}\right|(最大行和).\end{array}$$

（3）ky-Fan Norm

矩阵$A\in {\mathbb{R}}^{n\times m}$的ky-Fan范数定义如下：

对任意$A\in {\mathbb{R}}^{n\times m}$，其ky-Fan范数为：
$$\Vert A{\Vert }_{(k)}=\sum _{i=1}^k{\sigma }_i$$
其中${\sigma }_i$是$A$的第$i$大的奇异值( σ 1 ≥ σ 2 ≥ ? ≥ σ min ? { m , n } \sigma_1\geq\sigma_2\geq\cdots\geq \sigma_{\min\{m,n\}} σ1?≥σ2?≥?≥σmin{m,n}?).

如何证明这个定义确实是一个范数，第一二条的正定性和齐次性验证都比较简单，对于三角不等式的验证，可以利用优超不等式，具体查阅参考文献1.

k=1时，导出谱范数：
$$\Vert A{\Vert }_{(1)}={\sigma }_1(A)$$
另一个一个常用的是核范数，对$A\in {\mathbb{R}}^{n\times m}$，若$n?m$，其核范数为：
$$\begin{array}{r}\Vert A{\Vert }_{(m)}={\sigma }_1+?+{\sigma }_m(\text{?核范数?}).\end{array}$$

（4）Schatten norms

对任意$A\in {\mathbb{R}}^{n\times m}$(设m<n)，Schatten p-范数定义为：
$$\Vert A{\Vert }_p=[\sum _{j=1}^m({\sigma }_j(A){)}^p{]}^{1/p},1\le p<\infty ,$$

常见的Schatten p-范数如下：
$$\begin{array}{rl}\Vert A{\Vert }_1& =\sum _{i=1}^m{\sigma }_i\left(A\right)\left(\text{核范数}\right).\\ \Vert A{\Vert }_2& =\sqrt{\sum _{i=1}^m{\delta }_i^2\left(A\right)}\left(F?\text{范数}\right).\\ \Vert A{\Vert }_{\infty }& ={\sigma }_1\left(A\right),\left(\text{谱范数}\right).\end{array}$$
我们可以看到，由不同范数的定义，可以导出相同的范数。

（5）Unitarily invariant Norms

酉不变范数是指：

$\mathcal{X}$上的范数$\Vert ?\Vert$如果满足，对任意的$A\in {\mathbb{R}}^{m\times n}$，以及任意的酉矩阵$U,V$，都有：
$$\Vert UA{V}^T\Vert =\Vert A\Vert$$
则称$\Vert ?\Vert$是酉不变范数.

满足这个条件的范数有很好的性质，上面介绍的ky-Fan Norm和Schatten norms都是酉不变范数，所以由这两个范数定义导出的各种范数也是酉不变的，比如F-范数.

参考资料

1. Horn, Roger A., and Charles R. Johnson. Matrix analysis. Cambridge university press, 2012.