LeetCode-141环形链表 & LeetCode-142环形链表二
一、前言
本篇文章在我之前讲完的链表、链表与递归的基础上进行讲解,本次我们以leetcode为例,讲解链表的其他题型,今天我们先了解一下环形链表,这里我们以leetCode141和leetCode142为例。
二、LeetCode141
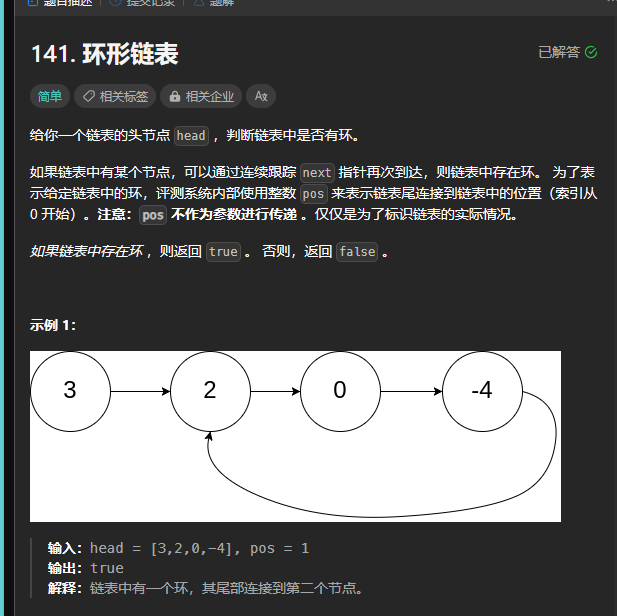
首先关于这道题,我们知道链表有着天然的递归性质,我们可以借助哈希表,如果链表有环,那么当通过环走到相同节点的时候,在哈希表一定能找到。所以对于递归求解,最基本的问题就是分为有环和无环,如果无环,那么当当前节点等于NULL,直接return false即可。如果有环,那么当hashSet找到此节点时,直接return true即可。然后把head.next作为参数调用递归函数即可。
代码如下:
public static boolean hasCycle(ListNode head) {
if (head == null || head.next == null) {
return false;
}
HashSet<ListNode> hashSet = new HashSet<>();
return hasCycleRecursion(hashSet,head);
}
private static boolean hasCycleRecursion(HashSet<ListNode> hashSet, ListNode head) {
if(head == null){
return false;
}
if(hashSet.contains(head)){
return true;
}
hashSet.add(head);
return hasCycleRecursion(hashSet,head.next);
}
那么这道题有没有更优解呢,答案是有的,这里我们就要介绍一种特殊的算法:快慢指针。
快慢指针的原理,就是让快慢指针同时从head出发,快指针一次走两格,而慢指针一次走一格。
如果链表无环,那么快指针肯定会走到NULL,从而快慢不可能相遇。如果链表有环,快慢指针都会陷入环中进行无限次移动,然后变成了追及问题。想象一下在操场跑步的场景,只要一直跑下去,快的总会追上慢的。因为它们的相差速度就是一,当两个指针都进入环后,每轮移动使得慢指针到快指针的距离增加一,同时快指针到慢指针的距离也减少一,只要一直移动下去,快指针总会追上慢指针。还不懂的话,我们以相对速度的角度去看,此时slow不动,fast每次以一的速度去追slow,那么这样肯定是能追上slow的。
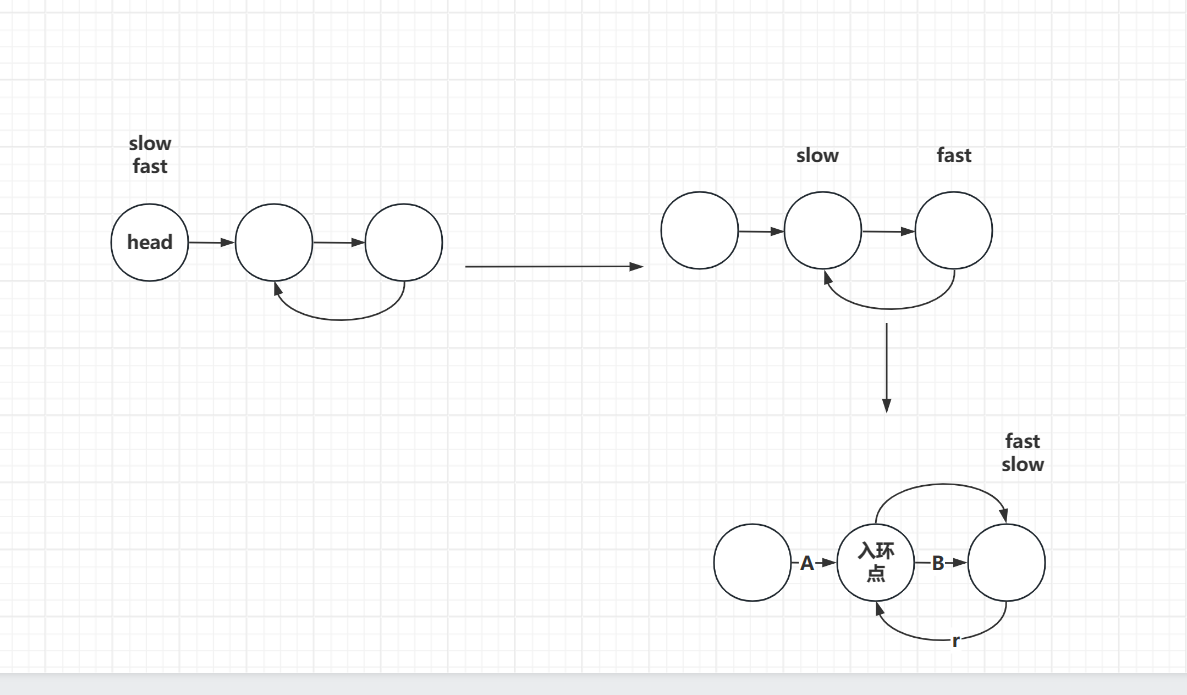
那么这样就很简单了,我们定义slow和fast都从head出发,只要fast.next和fast.next.next均不为空,那么就让slow和fast开始移动,如果在移动过程中slow==fast,那么就说明有环,否则无环:
public static boolean hasCycle(ListNode head) {
if(head == null){
return false;
}
ListNode slow = head;
ListNode fast = head;
while (fast.next != null && fast.next.next != null){
slow = slow.next;
fast = fast.next.next;
if(fast == slow){
return true;
}
}
return false;
}
有些人可能会问,快慢指针为什么快指针一定要是慢指针的两倍,我不可以是三倍吗
其实三倍也可以,只是反而可能拖累效率,推导如下
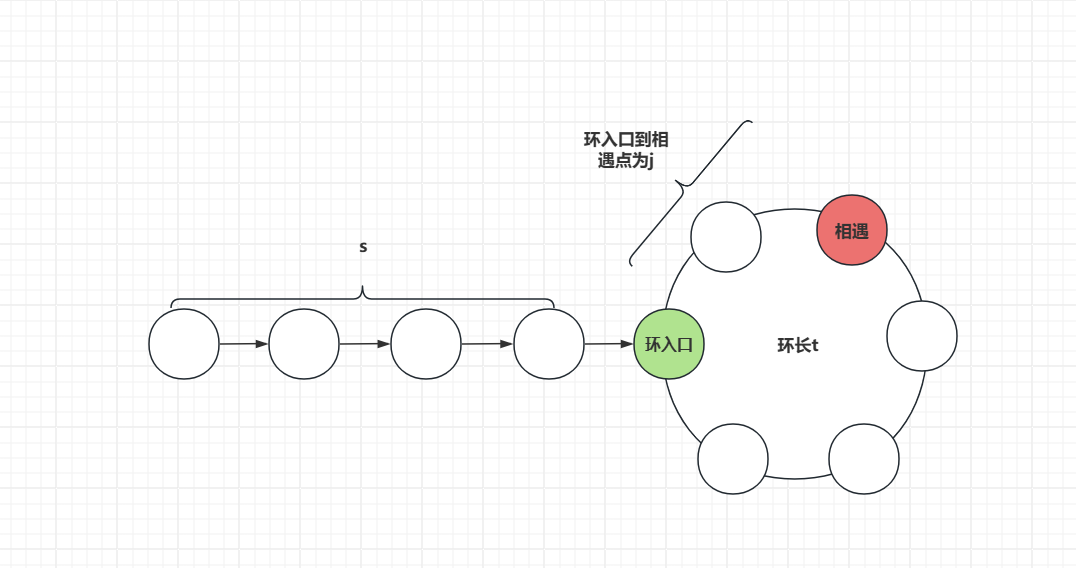
如上图,非环长s,环长t,环入口距离相遇点j,假设快指针比慢指针速度快k倍,当两者相遇,此时慢指针走了s+j,快指针走了
s+j+n*t(n为快指针在环中的圈数)。
那么有s+j+n*t=k(s+j),推导一下有(n*t)/(k-1)=s+j,也可以写为(n/k-1)*t = s+j
我们知道这个式子的参数一定都是整数,那么k-1也一定要是正整数,在其他量都确定的情况下,保持(n / k-1)不变的话,分母k-1越小,则分子n也越小,对应快指针在环中走的圈数n也越小,k=2,3,4···,其中k=2时,m最小,即最快相遇,这样效率最高。如果k=3,反而可能影响效率。
故我们快指针设定一次走两步。
三、LeetCode142
那么如果我们需要找到环入口该如何去做呢,拿LeetCode142为例:

做法一,其实上面的哈希表大家仔细想想,已经做完了这道题,当我发现哈希表重复的节点的时候,那个重复的节点就是环入口。
所以把141的代码稍微改下返回值就可以提交了:
public ListNode detectCycle(ListNode head) {
if(head == null || head.next == null){
return null;
}
HashSet<ListNode> listNodes = new HashSet<>();
return detectCycleRecursion(listNodes,head);
}
private ListNode detectCycleRecursion(HashSet<ListNode> listNodes, ListNode head) {
if(head == null){
return null;
}
if(listNodes.contains(head)){
return head;
}
listNodes.add(head);
return detectCycleRecursion(listNodes,head.next);
}
那么解法二自然还是之前的快慢指针了,我们首先定义快慢指针,然后沿用判环的代码,如果快慢指针相遇,说明有环,此时在这个基础上,我们来推导环的入口:
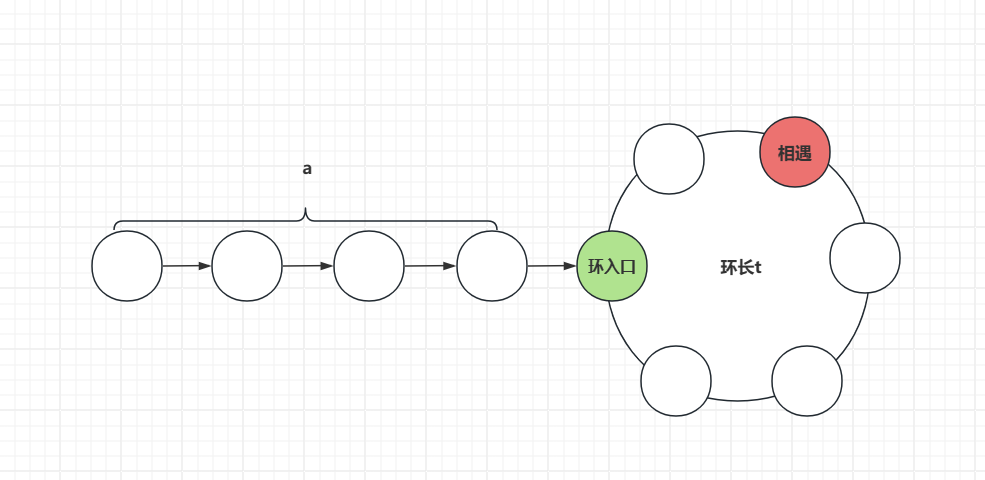
设a为head到环入口的距离,环长为t
此时快指针比慢指针多走nt步(因为slow和fast都走了a步),设立f为fast走的,s为slow走的,有f=2s,f=s+nt
由上面的结论可以得到s=nt,即慢指针走了nt距离
假设从链表头部一直向前走并统计步数k,那么所有 走到链表入口节点时的步数 是:k=a+nt
那么根据上面s=nt,头节点走到环入口是a+nt,我们只需要让慢指针再走a步即可达到环入口,而头节点距离环入口刚好是a。那么就是头节点和慢指针一起出发,相遇的节点就是环入口
所以当快慢指针相遇的时候,我们定义两个指针,分别从head和slow出发,一次走一步,相遇点就是环入口,代码如下:
public static ListNode detectCycle(ListNode head) {
if(head == null){
return null;
}
ListNode slow = head;
ListNode fast = head;
while (fast.next != null && fast.next.next != null){
slow = slow.next;
fast = fast.next.next.next;
if(slow == fast){
ListNode newSlow = slow;
ListNode newHead = head;
while (newSlow != newHead){
newSlow = newSlow.next;
newHead = newHead.next;
}
return newHead;
}
}
return null;
}
这里最后提一嘴,如果要求环长,首先当然还是可以用hash表,和上面思路一样,当发现一样的元素时,此时看哈希表的长度即可。
而另一种方法就是当快慢指针相遇时,由于此时肯定是有环的,我只需要让慢指针一格一格往前走,快指针不动,当慢指针再次和快指针相遇时,此时慢指针走的距离就是环长。这里代码就不做赘述,比较简单,大家可以自行实现。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!