算法每日一题:在链表中插入最大公约数 | 链表 | 最大公约数
发布时间:2024年01月06日
hello,大家好,我是星恒
今天的题目是有关链表和最大公约数的题目,比较简单,核心在于求解最大公约数,我们题解中使用辗转相除法来求解,然后我们会在最后给大家拓展一下求解最大公约数的四个方法,供大家学习
今日题目:
题目:
给你一个链表的头 head ,每个结点包含一个整数值。
在相邻结点之间,请你插入一个新的结点,结点值为这两个相邻结点值的 最大公约数 。
请你返回插入之后的链表。
两个数的 最大公约数 是可以被两个数字整除的最大正整数。
示例:
示例 1: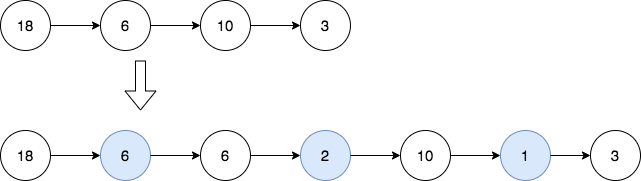
输入:head = [18,6,10,3]
输出:[18,6,6,2,10,1,3]
解释:第一幅图是一开始的链表,第二幅图是插入新结点后的图(蓝色结点为新插入结点)。
- 18 和 6 的最大公约数为 6 ,插入第一和第二个结点之间。
- 6 和 10 的最大公约数为 2 ,插入第二和第三个结点之间。
- 10 和 3 的最大公约数为 1 ,插入第三和第四个结点之间。
所有相邻结点之间都插入完毕,返回链表。
示例 2:
输入:head = [7]
输出:[7]
解释:第一幅图是一开始的链表,第二幅图是插入新结点后的图(蓝色结点为新插入结点)。
没有相邻结点,所以返回初始链表。
提示:
- 链表中结点数目在 [1, 5000] 之间。
- 1 <= Node.val <= 1000
分析:
本题的核心在于求最大公约数,求得最大公约数,我们将其连接到链表上就可以啦
辗转相除法,代码写法就是,两个数a,b相除取余c,将被除数b赋值个除数a,将余数c复制给被除数b,直到其余数c为0,也就是被除数b为0,这样,除数a就是他们的最大公约数!
题解:
class Solution {
public ListNode insertGreatestCommonDivisors(ListNode head) {
ListNode cur = head;
while (cur.next != null) {
cur.next = new ListNode(gcd(cur.val, cur.next.val), cur.next);
cur = cur.next.next;
}
return head;
}
int gcd(int a, int b) {
while (b != 0) {
int tmp = a % b;
a = b;
b = tmp;
}
return a;
}
}
拓展
求最大公约数
- 辗转相除法
public int gcd(int a, int b) {
while (b != 0) {
int temp = a % b;
a = b;
b = temp;
}
return a;
}
- 更相减损法
public int gcd(int a, int b) {
while (a != b)
{
if (a > b)
a -= b;
else
b -= a;
}
return a;
}
- 递归法
public int gcd(int a, int b) {
if (b == 0) return a;
return gcd(b, a % b);
}
如果大家有什么思考和问题,可以在评论区讨论,也可以私信我,很乐意为大家效劳。
好啦,今天的每日一题到这里就结束了,如果大家觉得有用,可以可以给我一个小小的赞呢,我们下期再见!
文章来源:https://blog.csdn.net/m0_61780691/article/details/135421666
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 力扣labuladong一刷day63天单词拆分
- MMBT3904-ASEMI智能灯具三极管MMBT3904
- OpenAI推出安全准备框架,解决AI模型的灾难性风险问题;2023年的生成AI进展和2024年的展望
- rhino犀牛怎么导入和调整背景图?
- 解决Reinitialized existing Git repository
- 【手撕C语言 第八集】函数栈帧的创建与销毁
- Python内部类
- 赦免战俘#洛谷
- 神经网络语言模型(Neural Network Language Model,NNLM)
- 小样本学习系列工作(持续更新)