代码随想录算法训练营第五十二天|300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组

代码随想录 (programmercarl.com)

300.最长递增子序列

1.dp数组及下标含义

dp[i]：表示以nums[i]为结尾的最长递增子序列的长度

2.递推公式

if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

3.初始化

每一个i，对应的dp[i]（即最长递增子序列）起始大小至少都是1，所以i从1开始进行遍历。

4.遍历顺序

i从前往后遍历，j的遍历顺序都可以，选择从前往后遍历。

最终是求出以每一个不同的nums[i]为结尾的最长递增子序列的长度，然后再求最大值。

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        int result = 1;
        Arrays.fill(dp, 1);//全部初始化为1，表示以nums[i]结尾的递增子序列长度至少是1
        for (int i = 1; i < nums.length; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]){
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            if (dp[i] > result){
                result = dp[i];
            }
        }
        return result;
    }
}

5.打印dp数组

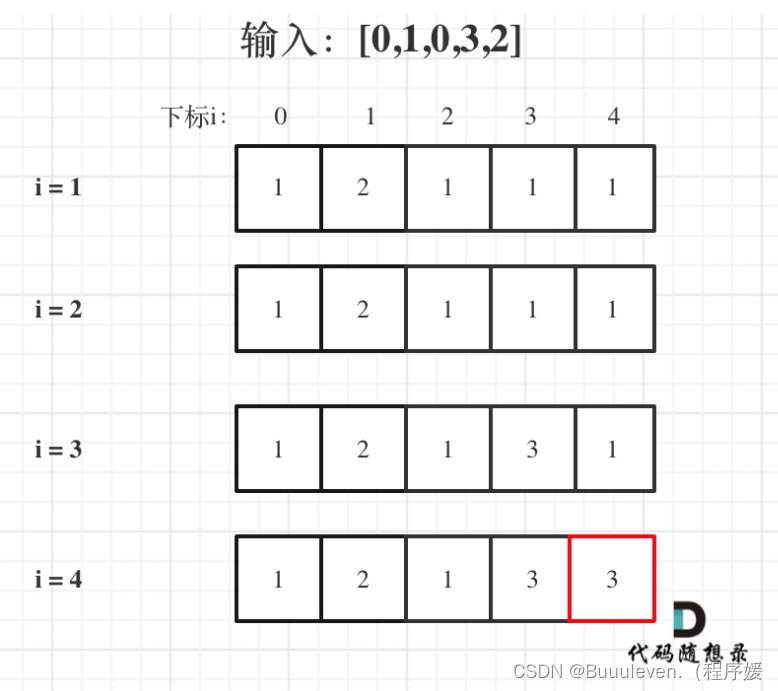
674. 最长连续递增序列

方法一：贪心算法

错误思路：贪心算法（以下为?错误代码

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int res = 1;
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] > nums[i - 1]){
                res++;
            }else break;
        }
        return res;
    }
}

此处没有考虑到前面顺序断了之后，最长连续递增序列可能在后面产生。

=====以下为?正确代码=====

遇到nums[i] > nums[i - 1]的情况，count就++，否则count为1（从头开始计数），记录count的最大值就可以了。

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        if (nums.length == 0){
            return 0;
        }
        int res = 1;
        int count = 1;
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] > nums[i - 1]){
                count++;
            }else{
                count = 1;//重新从头开始计数
            }
            if (count > res){//放在循环里面，让res保存每一次循环的最大count值
                res = count;
           }
        }
        return res;
    }
}

方法二：动态规划

用时和贪心算法差不多，此题和上一题在递推公式上有所区别，同时循环只需要一层for循环即可。

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int[] dp = new int[nums.length];
        int res = 1;
        Arrays.fill(dp, 1);
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] > nums[i - 1]){
                dp[i] = dp[i - 1] + 1;
            }
            if (dp[i] > res){
                res = dp[i];
            }
        }
        return res;
    }
}

718. 最长重复子数组?

1.dp数组及下标含义

dp[i][j]：表示以i - 1结尾的nums1和以j - 1结尾的nums2的最长重复子数组的长度。

不定义为表示以i结尾的nums1和以j结尾的nums2的最长重复子数组的长度，是为了后面初始化的时候更加方便。

如果这样定义，那么dp[i][0]和dp[0][j]就是有意义的，dp数组的第一行和第一列就不能直接默认初始化为0了。在初始化的时候需要考虑nums1的第一个元素与nums2的所有元素进行遍历对比（nums2的第一个元素与nums1的所有元素进行遍历对比），如果相等，则需要将对应的元素初始化为1，其余元素默认初始化为0，会很麻烦。

2.递推公式

if(nums1[i - 1] == nums2[j -1])? dp[i][j] = dp[i - 1][j - 1] + 1;

3.初始化

根据dp[i][j]的定义，dp[i][0] 和dp[0][j]其实都是没有意义的，根据递推公式可以看出，遍历i 和 j 要从1开始。

dp[i][0] = 0; dp[0][j] = 0;

4.遍历顺序

两层for循环，遍历nums1和nums2，最终结果需要遍历dp数组，求解最大值。

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];
        int res = 0;
        for (int i = 1; i <= nums1.length; i++) {
            for (int j = 1; j <= nums2.length; j++) {
                if (nums1[i - 1] == nums2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > res){
                    res = dp[i][j];//遍历寻找最长重复子数组的大小
                }
            }
        }
        return res;
    }
}

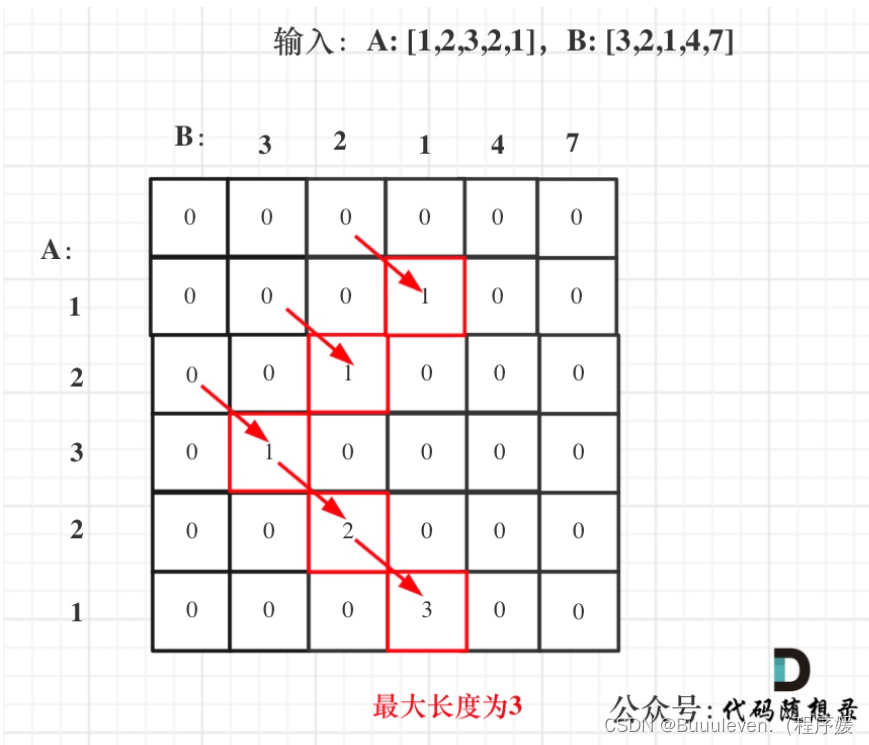
5.打印dp数组