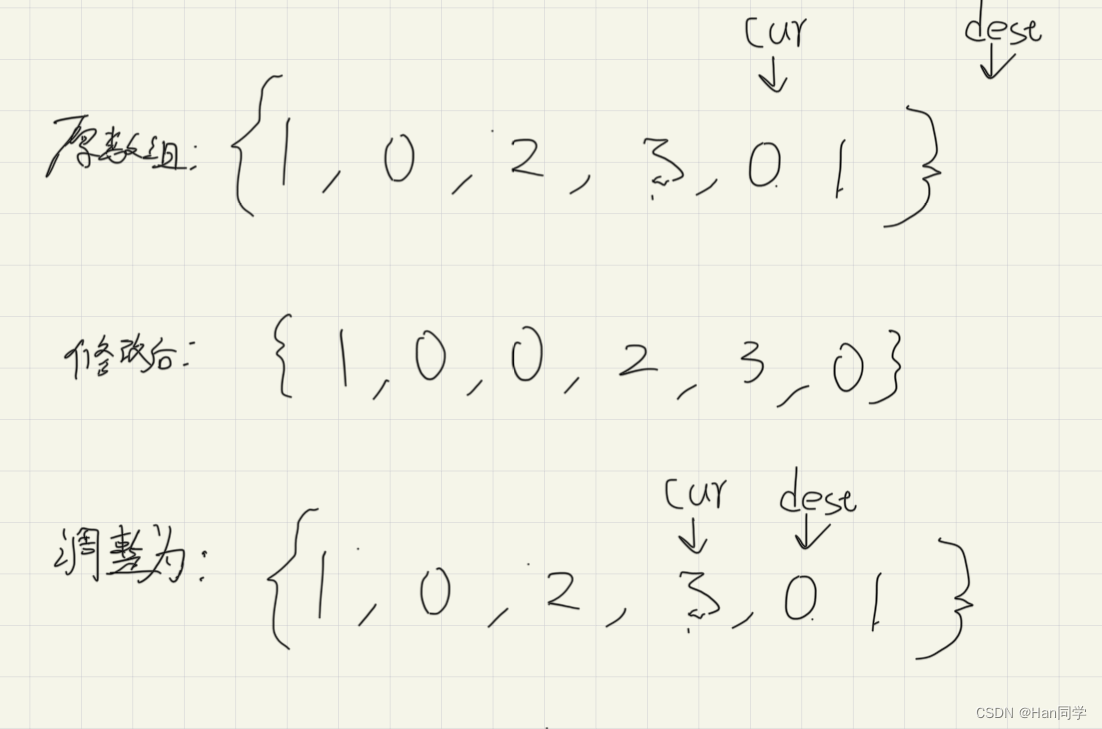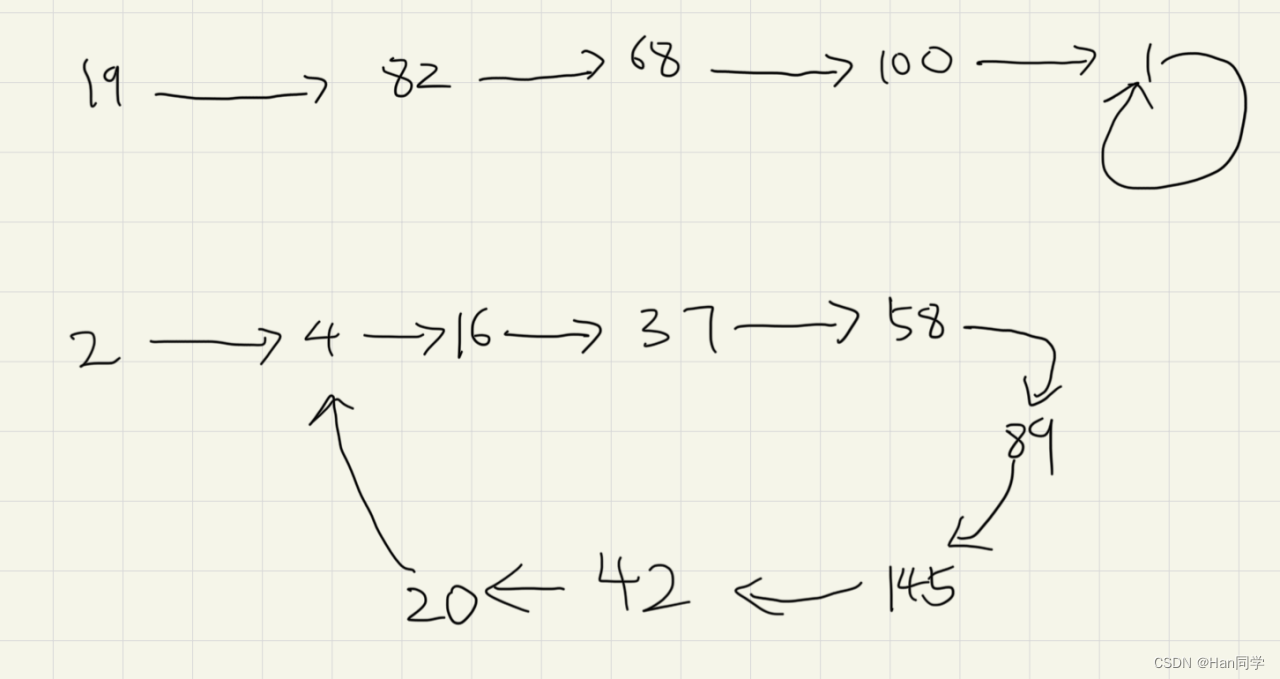C++ 双指针思路OJ题

目录

一、283. 移动零

二、1089. 复写零

三、202. 快乐数

四、11. 盛最多水的容器

五、611.有效三角形的个数

六、LCR 179. 查找总价格为目标值的两个商品

七、15. 三数之和

八、18. 四数之和

---

一、283. 移动零

思路：变量cur从零开始负责遍历数组，dest起始在-1位置，负责找到值为0的元素。遍历数组，当前元素值不为零，则交换dest和cur位置的值，dest后移一位，无论是否找到零元素，每次遍历后cur均后移一位。

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int cur = 0, dest = -1;
        while (cur < nums.size()) {
            if (nums[cur] != 0) {
                swap(nums[++dest], nums[cur]);
            }
            ++cur;
        }
    }
};

dest起始位置也可以从0开始 。

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int cur = 0, dest = 0;
        while (cur < nums.size()) {
            if (nums[cur] != 0) {
                swap(nums[dest++], nums[cur]);
            }
            ++cur;
        }
    }
};

二、1089. 复写零

?

?思路：首先cur找到修改后数组的最后一位元素，dest统计修改数组元素个数（大于等于原数组大小即cur找到修改后数组末尾元素），然后借助cur和dest位置，实现从后向前将非零元素后移一位，零元素后移一位，之后空出来的前项也赋值为零，还需处理特殊情况：desr大于数组元素个数时

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        int cur = 0, dest = -1, n = arr.size();
        while (cur < n) {
            if (arr[cur])
                dest++;
            else
                dest += 2;
            if (dest >= n - 1)
                break;
            ++cur;
        }
        if (dest == n) {
            arr[n - 1] = 0;
            dest -= 2;
            cur--;
        }
        while (cur >= 0) {
            if (arr[cur]) {
                arr[dest--] = arr[cur--];
            } else {
                arr[dest--] = 0;
                arr[dest--] = 0;
                cur--;
            }
        }
    }
};

三、202. 快乐数

?思路：快慢指针思想

class Solution {
public:
    int bitSum(int n) {
        int sum = 0;
        while (n) {
            int temp = n % 10;
            sum += temp * temp;
            n /= 10;
        }
        return sum;
    }
    bool isHappy(int n) {
        int slow = n, fast = n;
        do {
            slow = bitSum(slow);
            fast = bitSum(bitSum(fast));
        } while (slow != fast);
        return slow == 1;
    }
};

四、11. 盛最多水的容器

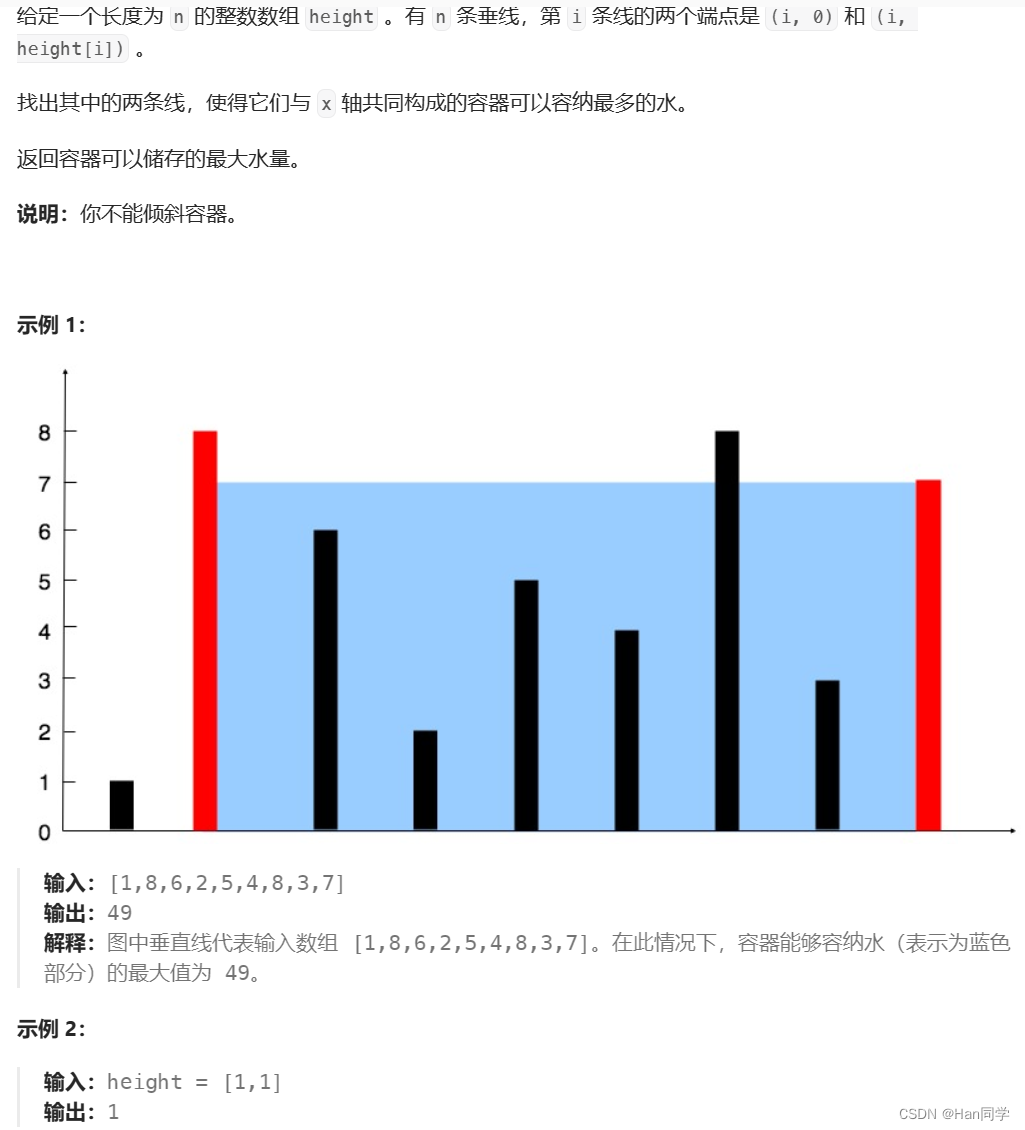
思路：初始位置从最左端和最右端开始，先计算一次容积，然后与上一次的容积相比求最大值，如果左端比右端小，则对左端后移一位，反之对右端前移一位，循环往复直到左右端相遇。?

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0, right = height.size() - 1, ret = 0;
        while (left < right) {
            int tmp = (right - left) * min(height[left], height[right]);
            ret = max(ret, tmp);
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        return ret;
    }
};

五、611.有效三角形的个数

思路：

1. 首先对数组排序，以便利用有序数组(升序)的单调性。
2. 外层从后往前（大到小）遍历作为三角形的第三条边，内层以数组索引为0的值即最左端，作为其中一条边。
3. 以每次第三条边的前一个位置即右端，作为其中一条边，对两边相加之和与第三条边作比较，如果大于第三边，则左端到右端范围内与右端和第三边的组合均为有效的三角形组合，接着右端后移一位。如果小于第三边，则左端后移一位(增大)，以此规则循环找出所有适合当前第三边的组合。

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int ret = 0, n = nums.size();
        for (int i = n - 1; i >= 2; i--) {
            int left = 0, right = i - 1;
            while (left < right) {
                if (nums[left] + nums[right] > nums[i]) {
                    ret += right - left;
                    right--;
                } else {
                    left++;
                }
            }
        }
        return ret;
    }
};

六、LCR 179. 查找总价格为目标值的两个商品

思路：利用有序数组的单调性，从数组最左和最右分别开始求和，与目标值相比较，如果小于目标值则最左位置后移一位（增大以接近目标值），如果大于目标值则最右向前一位（减小以接近目标值）。

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        int left = 0, right = price.size() - 1;
        while (left < right) {
            int sum = price[left] + price[right];
            if (sum < target) {
                left++;
            } else if (sum > target) {
                right--;
            } else {
                return {price[left], price[right]};
            }
        }
        return {-1, -1};
    }
};

• {price[left], price[right]}表示一个初始化了两个元素的向量（vector），{-1, -1}也是一个初始化了两个元素的向量，这种用法可以方便地返回多个值或结果。
• 在C++中，使用花括号{}可以用于初始化数组、向量和其他容器类型的对象。在这个特定的情况下，通过使用花括号初始化向量，可以直接返回一个包含两个元素的向量作为函数的返回值。

七、15. 三数之和

?思路：1、排序? 2、双指针

每次固定一个数，从该数后一位到最后这段区间内找到两个数，其相加之和等于该数的相反数即符合要求，注意处理越界和重复问题。

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> ret;
        sort(nums.begin(), nums.end());
        int n = nums.size();
        for (int i = 0; i < n;) {
            if (nums[i] > 0)
                break;
            int left = i + 1, right = n - 1, target = -nums[i];
            while (left < right) {
                int sum = nums[left] + nums[right];
                if (sum > target)
                    right--;
                else if (sum < target)
                    left++;
                else {
                    ret.push_back({nums[i], nums[left], nums[right]});
                    left++, right--;
                    while (left < right && nums[left] == nums[left - 1])
                        left++;
                    while (left < right && nums[right] == nums[right + 1])
                        right--;
                }
            }
            ++i;
            while (i < n && nums[i] == nums[i - 1])
                i++;
        }
        return ret;
    }
};

八、18. 四数之和

思路：排序+双指针，每次固定两个数，从第二个数往后的区间内，分别从左端和右端计算求和，寻找和等于目标值减去已固定两数的组合即为一个满足条件的四元组。

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> ret;
        if (nums.size() < 4)
            return ret; // 处理数组长度小于4的情况
        sort(nums.begin(), nums.end());
        int n = nums.size();
        for (int i = 0; i < n;) {
            for (int j = i + 1; j < n;) {
                int left = j + 1, right = n - 1;
                long long aim = (long long)target - nums[i] - nums[j];
                while (left < right) {
                    int sum = nums[left] + nums[right];
                    if (sum > aim)
                        right--;
                    else if (sum < aim)
                        left++;
                    else {
                        ret.push_back(
                            {nums[i], nums[j], nums[left++], nums[right--]});
                        while (left < right && nums[left] == nums[left - 1])
                            left++;
                        while (left < right && nums[right] == nums[right + 1])
                            right--;
                    }
                }
                j++;
                while (j < n && nums[j] == nums[j - 1])
                    j++;
            }
            i++;
            while (i < n && nums[i] == nums[i - 1])
                i++;
        }
        return ret;
    }
};