C++力扣题目239--滑动窗口最大值
给你一个整数数组?nums,有一个大小为?k?的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的?k?个数字。滑动窗口每次只向右移动一位。
返回?滑动窗口中的最大值?。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1 输出:[1]
思路:
这是使用单调队列的经典题目。
难点是如何求一个区间里的最大值呢? (这好像是废话),暴力一下不就得了。
暴力方法,遍历一遍的过程中每次从窗口中再找到最大的数值,这样很明显是O(n × k)的算法。
暴力代码:(会超出时间限制)
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int>max;
for (int back = 0, front = back + k-1; front < nums.size(); back++, front++)
{
int tmp=nums[back];
for (int i = 1; i < k; i++)
{
if (tmp < nums[back + i])
{
tmp = nums[back + i];
}
}
max.push_back(tmp);
}
return max;
}
};有的同学可能会想用一个大顶堆(优先级队列)来存放这个窗口里的k个数字,这样就可以知道最大的最大值是多少了,?但是问题是这个窗口是移动的,而大顶堆每次只能弹出最大值,我们无法移除其他数值,这样就造成大顶堆维护的不是滑动窗口里面的数值了。所以不能用大顶堆。
此时我们需要一个队列,这个队列呢,放进去窗口里的元素,然后随着窗口的移动,队列也一进一出,每次移动之后,队列告诉我们里面的最大值是什么。
这个队列应该长这个样子:
class MyQueue {
public:
void pop(int value) {
}
void push(int value) {
}
int front() {
return que.front();
}
};
每次窗口移动的时候,调用que.pop(滑动窗口中移除元素的数值),que.push(滑动窗口添加元素的数值),然后que.front()就返回我们要的最大值。
这么个队列香不香,要是有现成的这种数据结构是不是更香了!
其实在C++中,可以使用 multiset 来模拟这个过程,文末提供这个解法仅针对C++,以下讲解我们还是靠自己来实现这个单调队列。
然后再分析一下,队列里的元素一定是要排序的,而且要最大值放在出队口,要不然怎么知道最大值呢。
但如果把窗口里的元素都放进队列里,窗口移动的时候,队列需要弹出元素。
那么问题来了,已经排序之后的队列 怎么能把窗口要移除的元素(这个元素可不一定是最大值)弹出呢。
大家此时应该陷入深思.....
其实队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。
那么这个维护元素单调递减的队列就叫做单调队列,即单调递减或单调递增的队列。C++中没有直接支持单调队列,需要我们自己来实现一个单调队列
不要以为实现的单调队列就是 对窗口里面的数进行排序,如果排序的话,那和优先级队列又有什么区别了呢。
来看一下单调队列如何维护队列里的元素。
动画如下:
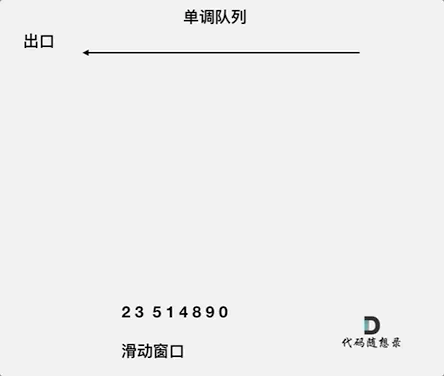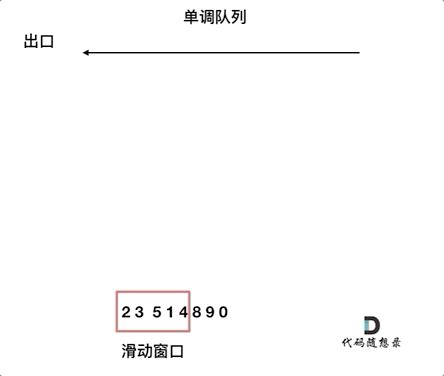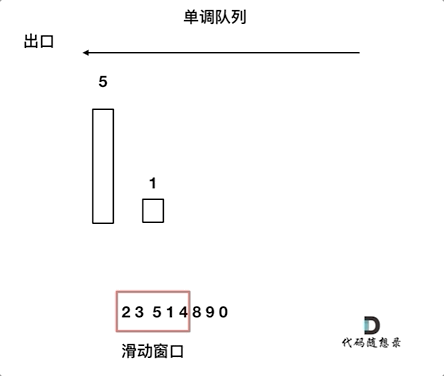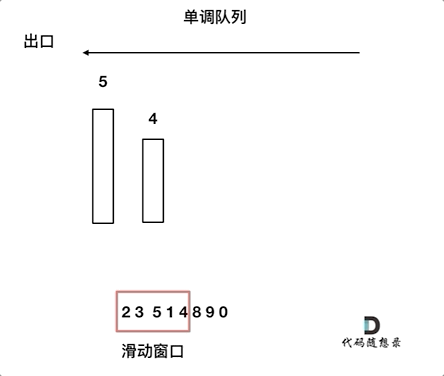
对于窗口里的元素{2, 3, 5, 1 ,4},单调队列里只维护{5, 4} 就够了,保持单调队列里单调递减,此时队列出口元素就是窗口里最大元素。
此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口进行滑动呢?
设计单调队列的时候,pop,和push操作要保持如下规则:
- pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
- push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
为了更直观的感受到单调队列的工作过程,以题目示例为例,输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3,动画如下:
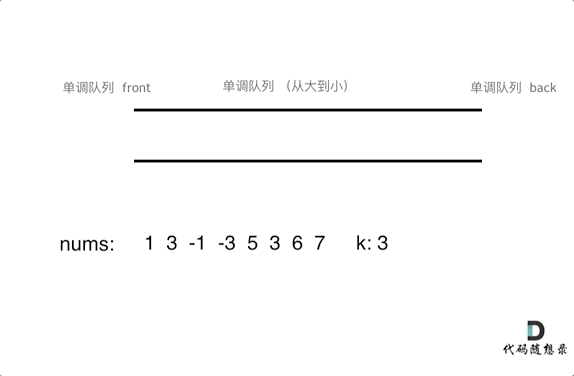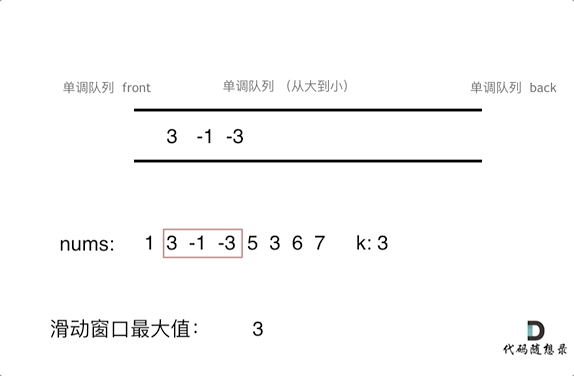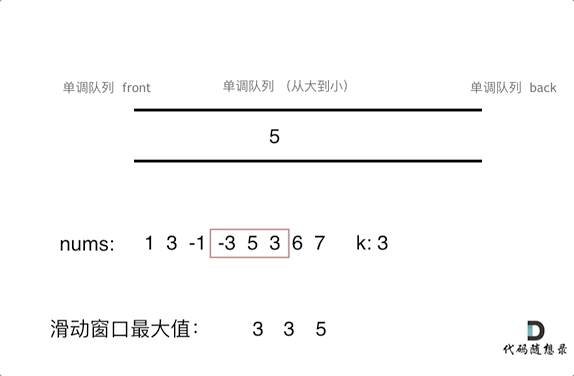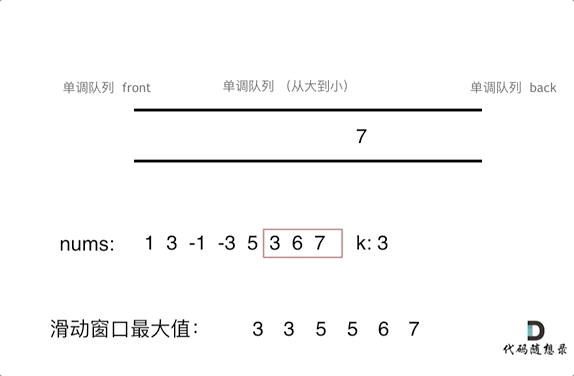
那么我们用什么数据结构来实现这个单调队列呢?
使用deque最为合适,常用的queue在没有指定容器的情况下,deque就是默认底层容器。
class Solution {
public:
class Mydeque
{
public:
deque<int>que;//创建一个从大到小的单调队列
void pop(int val)
{
if (!que.empty() && val == que.front())//只有当滑动窗口的最大值为第一个元素时
{ //才从这个单调队列从移除元素
que.pop_front();
}
}
void push(int val)//如果添加元素比前面元素大,将前面元素都尾删
{
while (!que.empty() && que.back() < val)
{
que.pop_back();
}
que.push_back(val);//将该元素尾插到deque中
}
int front()
{
return que.front();
}
};
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
Mydeque que;//声明一个自定义的单调队列
vector<int>result;
for (int i = 0;i < k; i++)//将前k个元素添加到队列
{
que.push(nums[i]);
}
result.push_back(que.front());//将第一个窗口最大值添加到结果容器
for (int i = k; i < nums.size(); i++)
{
que.pop(nums[i-k]);//滑动窗口移除最前面元素
que.push(nums[i]);//滑动窗口加入最后的元素
result.push_back(que.front());//将当前滑动窗口的最大值添加到结果容器中
}
return result;
}
};再来看一下时间复杂度,使用单调队列的时间复杂度是 O(n)。
有的同学可能想了,在队列中 push元素的过程中,还有pop操作呢,感觉不是纯粹的O(n)。
其实,大家可以自己观察一下单调队列的实现,nums 中的每个元素最多也就被 push_back 和 pop_back 各一次,没有任何多余操作,所以整体的复杂度还是 O(n)。
空间复杂度因为我们定义一个辅助队列,所以是O(k)。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!