除法器原理之恢复余数法
发布时间:2024年01月21日
本文全程将以 124除以3 为例进行求商和取模过程的讲解
被除数:dividend
除数:divisor
商:quotient
余数:remainder
手写除法过程
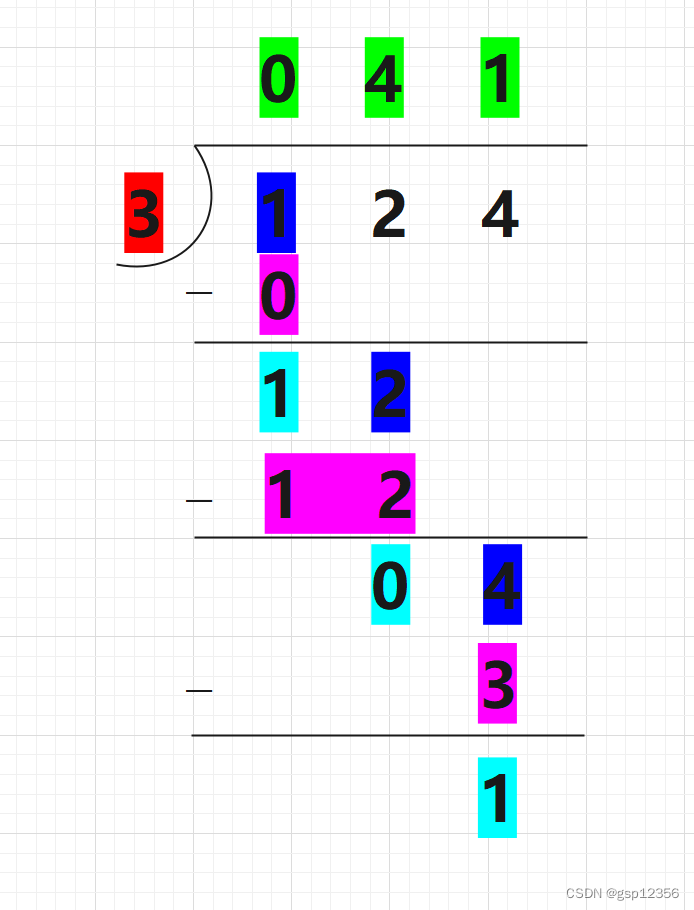
手写除法过程如上图所示:
N:被除数 124
D:除数 3
Q: 商 041
余数:1
被除数的位宽为3(10进制),商的位宽与被除数的位宽相同。
除数的位宽为1,余数的位宽与除数的位宽相同。
在求解Q[2]时,由于除数百位数为1,当Q[2]=1时,Q[2]*3=3>1,所以,Q[2]=0,且余数为1。
在求解Q[1]时,由于余数为1,十位数为2,部分余数为12。当Q[1]=5时,Q[1]*3=15>12,当Q[1]=4时,Q[1]*3=12,刚好相等,余数为0。
在求解Q[0]时,由于余数为0,个位为4,部分余数为4。当Q[0]=2时,Q[0]*3=6>4,所以Q[0]=1,余数为1。
在十进制除法中,商数Q[i]有10种可能(0~9),求解每一个商数即从中0-9中选出一个最大的数,通过选择一个商数Q[i]满足以下条件,设部分余数为psum:
0 <= (psum[i] - Q[i]*D)< D
psum[i-1] = psum[i] - Q[i]*D
R = psum[0]
恢复余数法计算过程
流程图如下:
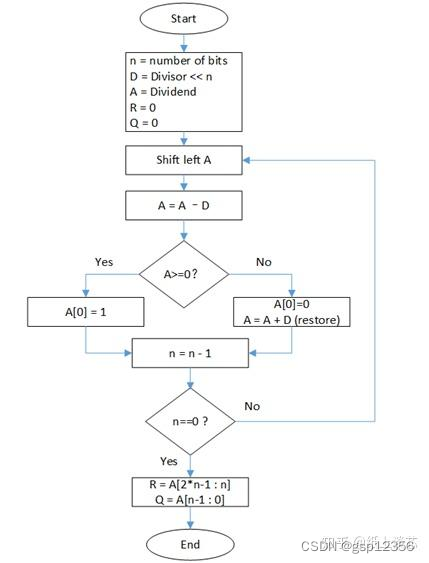
下面的计算以及取位数时的计算单位均为十进制,可以对比参考文献中的二进制,以此加强理解。
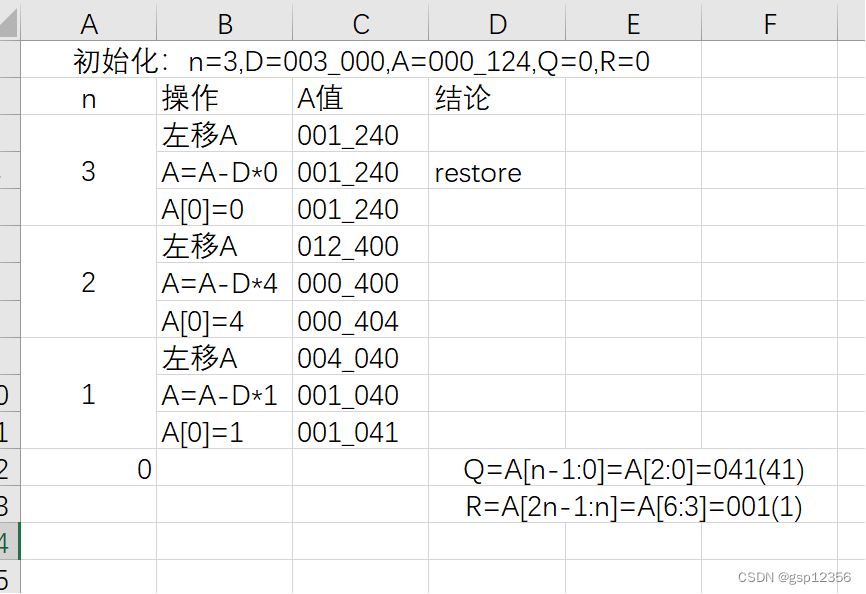
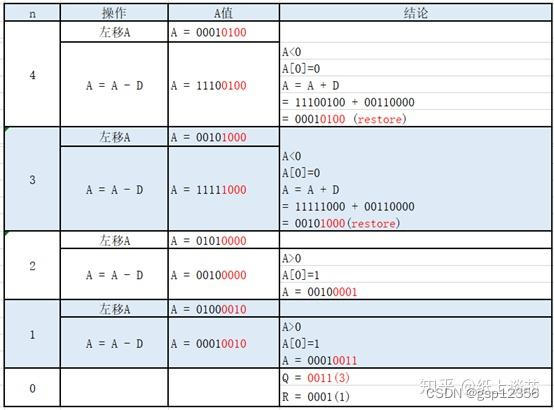
二进制的计算:
求被除数N=10,除数D=3的商Q和余数R?
10的二进制为1010
3的二进制为0011
初始化如下:
n = 4
D = 00110000
A = 00001010
R = 0000
Q = 0000
参考文献
https://zhuanlan.zhihu.com/p/164633088
文章来源:https://blog.csdn.net/gsp12356/article/details/135730290
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Java 重载 注解
- 【游戏篇】Scratch之饥饿的鱼
- 关于去游乐园排队因为人太多于是开始数情侣对数这件事
- 为什么学C语言和做底层的工作不好找,工资还没做Java的高?
- 如何推动智能制造 - 数字孪生示例
- 企业级软件定制开发如何提升用户体验
- 高德地图loca可视化脉冲流动线条
- 饥荒Mod 开发(二二):显示物品信息
- 使用Flink处理Kafka中的数据
- Pointnet++改进:在特征提取模块加入SegNext_Attention注意力机制,卷积注意力打造高性能点云分割模型