【C/C++笔试练习】排序时间复杂度、单链表、单循环链表、栈的应用、循环队列、完全二叉树的性质、哈夫曼树的构造、小根堆、哈希冲突、基数排序、年终奖、迷宫问题
文章目录
C/C++笔试练习
选择部分
(1)排序时间复杂度
??请指出选择排序,冒泡排序,快速排序的时间复杂度分别是()
??A. O(n2)、O(n2)、O(nlog2n)
??B. O(nlog2n)、、O(n2)、O(nlog2n)
??C. O(n)、O(n2)、O(n2)
??D. O(nlog2n)、O(n2)、O(n2)
??答案:A
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n) | O(n2) | O(1) | 稳定 |
| 简单选择排序 | O(n2) | O(n2) | O(n2) | O(1) | 不稳定 |
| 直接插入排序 | O(n2) | O(n) | O(n2) | O(1) | 稳定 |
| 希尔排序 | O(nlogn)~O(n2) | O(n1.3) | O(n2) | O(1) | 不稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 快速排序 | O(nlogn) | O(nlogn) | O(n2) | O(logn)~O(n) | 不稳定 |
??
(2)单链表
??在单链表中,增加头结点的目的是()
??A. 标识表结点中首结点的位置
??B. 算法实现上的方便
??C. 使单链表至少有一个结点
??D. 说明单链表是线性表的链式存储实现
??答案:B
??在单链表中增加头结点的目的是为了算法实现上的方便。具体来说,头结点可以作为哨兵,简化代码,避免空指针异常,并使得单链表的插入和删除操作更加统一和方便。
??
(3)单循环链表
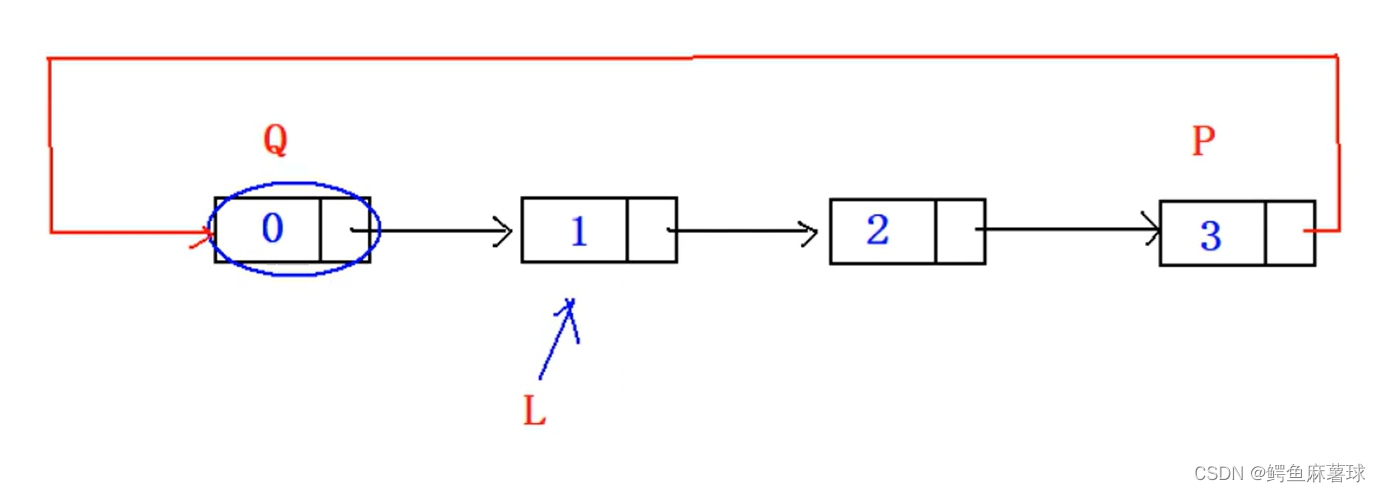
??下列算法的功能是什么?
/*L是无头节点单链表*/
LinkList Demo(LinkList L){
ListNode *Q,*P;
if(L&&L->next){
Q=L;
L=L->next;
P=L;
while(P->next)
P=P->next;
p->next=Q;
}
return L;
}
??A. 遍历链表
??B. 链表深拷贝
??C. 链表反转
??D. 单链表转变为循环链表
??答案:D
??上面的代码先用Q指针指向链表的第一个节点,再让指针P指向L的后面一个节点,while循环让P找到链表的最后一个节点的位置,最后将链表最后一个节点和之前保留的第一个节点连接,使这个单链表变成单循环链表,返回L。
??
(4)栈的应用
??表达式3 * 2 ^ (4 + 2 * 2 - 6 * 3) - 5求值过程中当扫描到6时,对象栈和运算符栈为(),其中^为乘幂
??A. 3,2,4,1,1;( * ^ ( +* -
??B. 3,2,8;( * ^ -
??C. 3,2,4,2,2;( * ^ ( -
??D. 3,2,8;* ^ ( -
??答案:D
??如果操作符的优先级大于运算符栈的优先级,则入栈;否则出栈进行计算。如果是同级别的则谁先入栈就计算谁。
| 对象栈 | 运算符栈 | 进行的操作 |
|---|---|---|
| 3 | * | 3 * 入栈 |
| 3 2 | * ^ | 2 ^入栈 |
| 3 2 4 | * ^ ( | 4 ( 入栈 |
| 3 2 4 2 | * ^ ( + | 2 + 入栈 |
| 3 2 4 2 2 | * ^ ( + * | 减优先级小于乘 2 * 2=4 加入对象栈 |
| 3 2 4 4 | * ^ ( + | 减优先级等于加 加先入栈 4+4=8 加入对象栈 |
| 3 2 8 | * ^ ( - | - 入栈 |
??所以对象栈的元素为:3 2 8 ;运算符栈的元素为:* ^ ( - 。
??
(5)循环队列
??假设以数组A[60]存放循环队列的元素,其头指针是front=47,当前队列有50个元素,则队列的尾指针值为()
??A. 3
??B. 37
??C. 97
??D. 50
??答案:B
??数组A[60]存放循环队列的元素。头指针front=47。当前队列有50个元素。由于队列中已有50个元素,根据循环队列的性质,尾指针的值可以通过以下方式计算:
??尾指针的位置 = 头指针的位置 + 队列中元素的数量;此时计算的值为47+50=97,由于循环队列中只有60个元素,所以对97%60=37, 即可计算出答案。
??
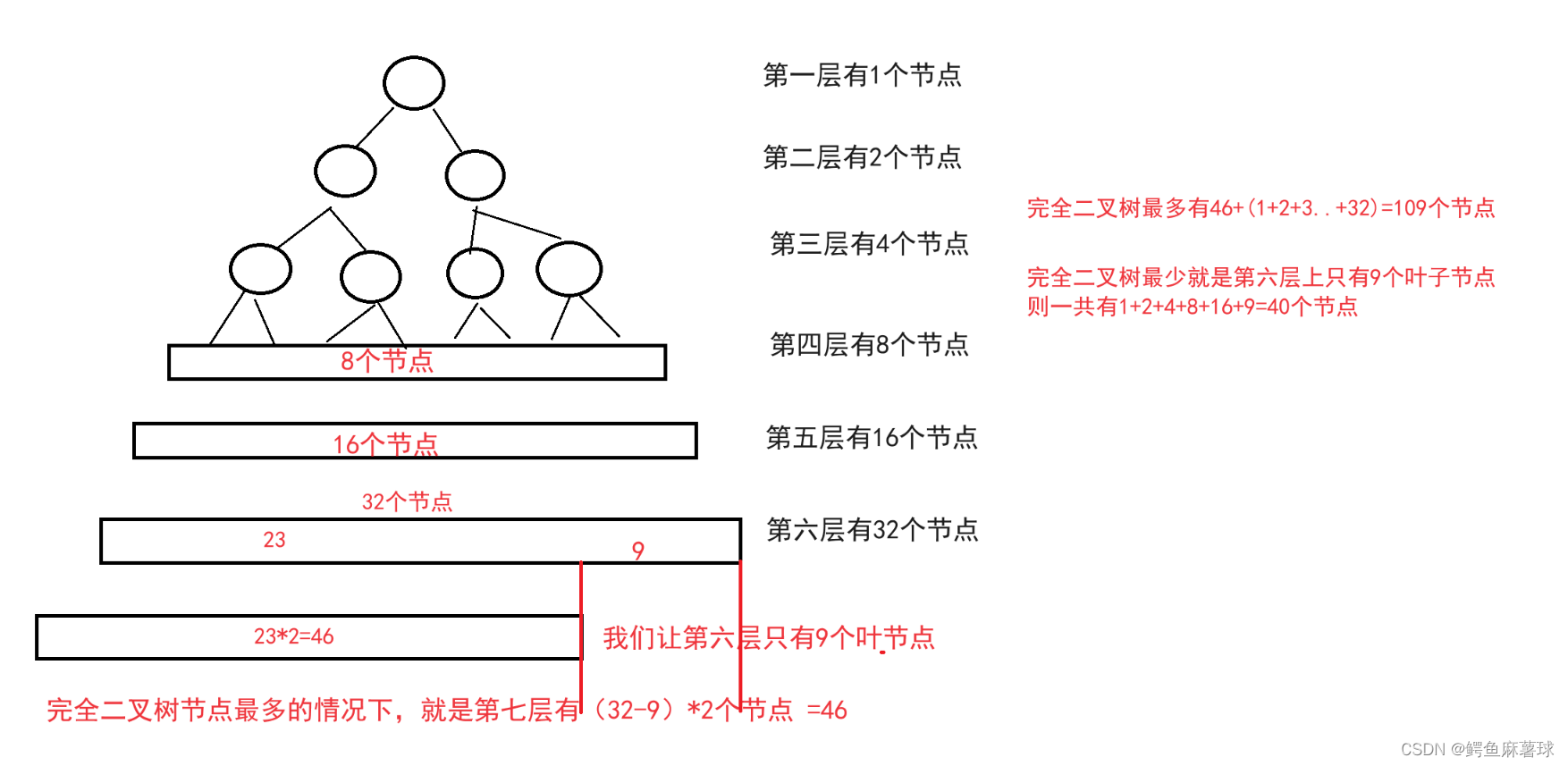
(6)完全二叉树的性质
??一棵完全二叉树第六层有9个叶结点(根为第一层),则结点个数最多有()
??A. 112
??B. 111
??C. 107
??D. 109
??答案:D
??
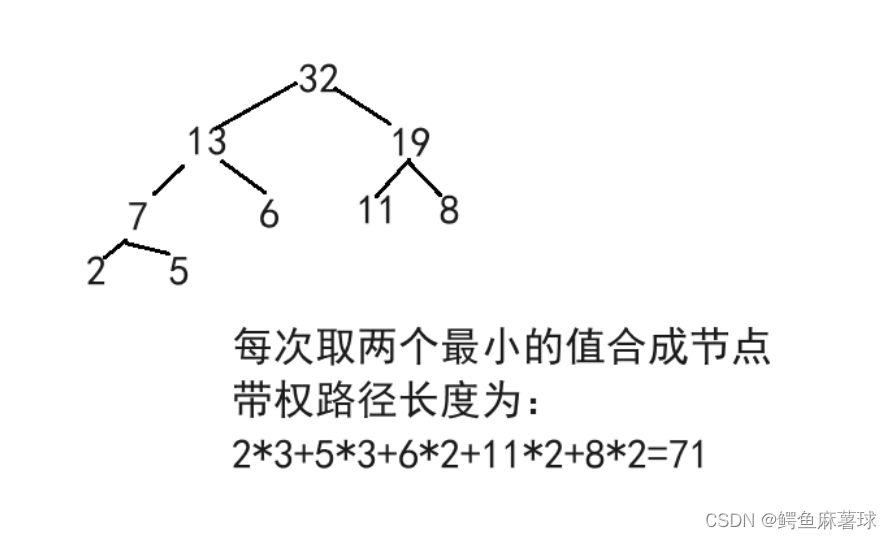
(7)哈夫曼树的构造
??有权值分别为11,8,6,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为()
??A. 24
??B. 71
??C. 48
??D. 53
??答案:B
??
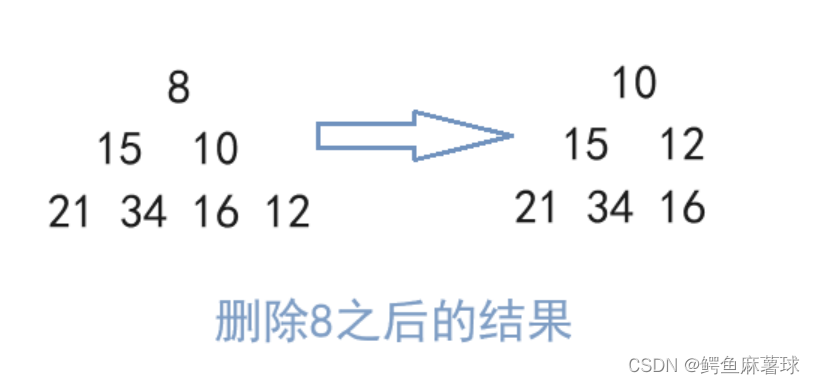
(8)小根堆
??已知小根堆为8,15,10,21,34,16,12,删除关键字8之后需重建堆,最后的叶子节点为()
??A. 34
??B. 21
??C. 16
??D. 12
??答案:C
??
(9)哈希冲突
??将10个元素散列到100000个单元的哈希表中,则()产生冲突
??A. 一定会
??B. 一定不会
??C. 仍可能会
??答案:C
??哈希表是一种通过将键(key)映射到数组中的位置来存储数据的数据结构。如果两个键被哈希函数映射到同一个位置,那么就会发生冲突。
??当我们有10个元素需要被散列到100000个单元的哈希表中。即使这个哈希表足够大,但是也无法保证每个元素都被随机地散列到表中,仍然有可能发生冲突,不同的键还是有可能会被哈希函数映射到相同的位置。
??
(10)基数排序
??下列排序算法中,元素的移动次数与关键字的初始排列次序无关的是 () 。
??A. 直接插入排序
??B. 起泡排序
??C. 基数排序
??D. 快速排序
??答案:C
??基数排序的比较和移动元素次数与初始排列次序无关,因为它是基于关键字的最低位进行排序的。
????????????
编程题 day24
年终奖
??解题思路:本题需要使用动态规划求解。定义f(i,j)表示从左上角走到坐标(i,j)处能获得的最大奖励。搜索所有从左上角走到右下角的路径,找到最优路径。
??f(i,j)分三种情况:
??第一列:f(i, 0) = f(i-1, 0) + board(i, 0)
??第一行:f(0,j) = f(0, j - 1) + b(0, j)
??其它位置:f(i, j) = max{f(i-1, j), f(i, j - 1)} + board(i, j)
??最后返回右下角的值。
class Bonus {
public:
int getMost(vector<vector<int> > board) {
int row = board.size();
int col = board[0].size();
vector<vector<int>> allPrice(row, vector<int>(col, 0));
allPrice[0][0] = board[0][0];
for (int i = 0; i < row; ++i)
{
for (int j = 0; j < col; ++j)
{
//如果是起点坐标,不做任何处理。
if (i == 0 && j == 0)
continue;
if (i == 0) //在第一行,只能往右走
allPrice[i][j] = allPrice[i][j - 1] + board[i][j];
else if (j == 0) //在第一列,只能往下走
allPrice[i][j] = allPrice[i - 1][j] + board[i][j];
else
//除去两个临界边,剩下的就是既能向右走,也能向下走,
//这时候就要考虑走到当前点的所有可能得情况,也就是走到当前点
//各自路径的和是不是这些所有到达该点路径当中最大的了
allPrice[i][j] = max(allPrice[i][j - 1], allPrice[i - 1][j]) + board[i][j];
}
}
// 返回最后一个坐标点的值,它就表示从左上角走到右下角的最大奖励
return allPrice[row - 1][col - 1];
}
};
??
迷宫问题
??解题思路:本题可用回溯法求解,具体步骤为:首先将当前点加入路径,并设置为已走,判断当前点是否为出口,是则输出路径,保存结果;跳转到4,依次判断当前点的上、下、左、右四个点是否可走,如果可走则递归走该点,当前点推出路径,设置为可走。
#include<iostream>
#include<vector>
using namespace std;
int ROW, COL;
vector<vector<int>> maze;
vector<vector<int>> path_tmp; //临时路劲
vector<vector<int>> path_best; //最佳路劲
void MazeTrack(int i, int j)
{
maze[i][j] = 1; //代表(i,j)已经走过
path_tmp.push_back({i, j});
//判断是否到达出口
if (i == ROW - 1 && j == COL - 1)
{
//寻找最短路劲
if (path_best.empty() || path_best.size() > path_tmp.size())
path_best = path_tmp;
}
//向右走
if (j + 1 < COL && maze[i][j + 1] == 0)
MazeTrack(i, j + 1);
//向左走
if (j - 1 >= 0 && maze[i][j - 1] == 0)
MazeTrack(i, j - 1);
//向上走
if (i - 1 >= 0 && maze[i - 1][j] == 0)
MazeTrack(i - 1, j);
//向下走
if (i + 1 < ROW && maze[i + 1][j] == 0)
MazeTrack(i + 1, j);
maze[i][j] = 0; //回溯 恢复路劲
path_tmp.pop_back();
}
int main()
{
while (cin >> ROW >> COL)
{
maze = vector<vector<int>>(ROW, vector<int>(COL,0));
//开辟迷宫空间path_tmp.clear();
path_best.clear();
//首先输入迷宫
for (int i = 0; i < ROW; ++i)
{
for (int j = 0; j < COL; ++j)
cin >> maze[i][j];
}
MazeTrack(0, 0); //从起始点(0,0)开始走
//输出路径
for (int i = 0; i < path_best.size(); ++i)
{
cout << "(" << path_best[i][0] << "," << path_best[i][1] << ")" << endl;
}
}
return 0;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!