拓扑排序
发布时间:2023年12月31日
目录
拓扑排序
-
一个有向图,如果图中有入度为 0 的点,就把这个点删掉,同时也删掉这个点所连的边。
-
一直进行上面出处理,如果所有点都能被删掉,则这个图可以进行拓扑排序。
举例子:
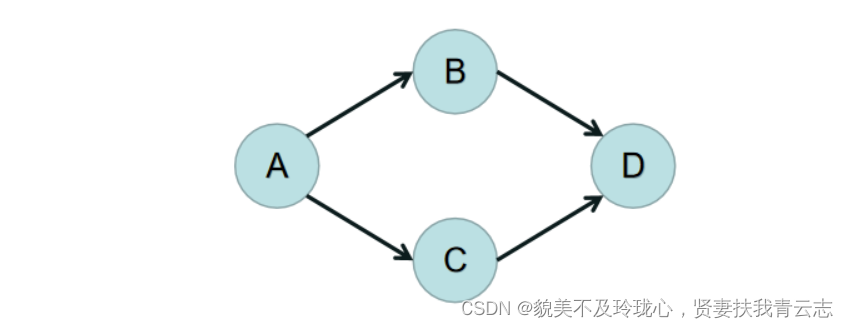
开始时,图是这样的状态,发现A的入度为 0,所以删除A和A上所连的边,结果如下图:
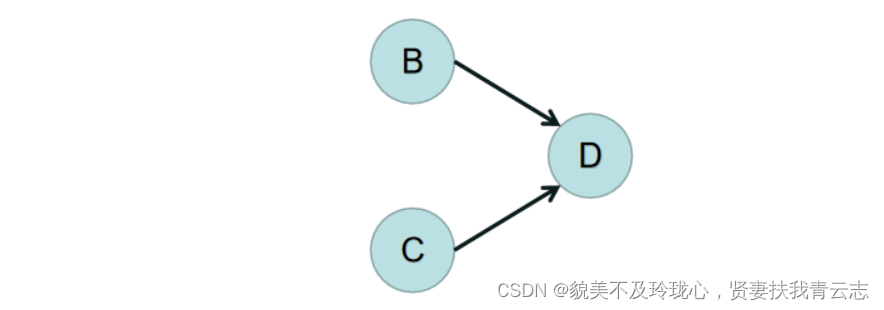
这时发现B的入度为 0,C的入度为 0,所以删除B和B上所连的边、C和C上所连的边,结果如下图:
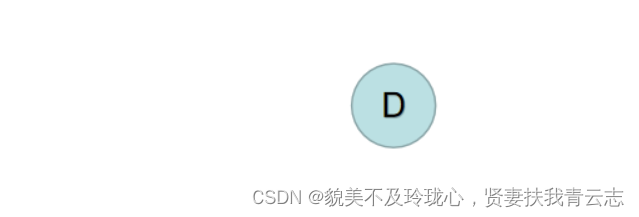
这时发现发现D的入度为 0,所以删除D和D上所连的边(如果有就删)。
-
所有的边都是从前指向后的
-
有向图才有拓扑排序
-
图中有环,一定没有拓扑排序
-
一个有向无环图一定是由一个拓扑排序的
-
一个有向无环图,一定存在一个入度为0的点
有向图的拓扑排序
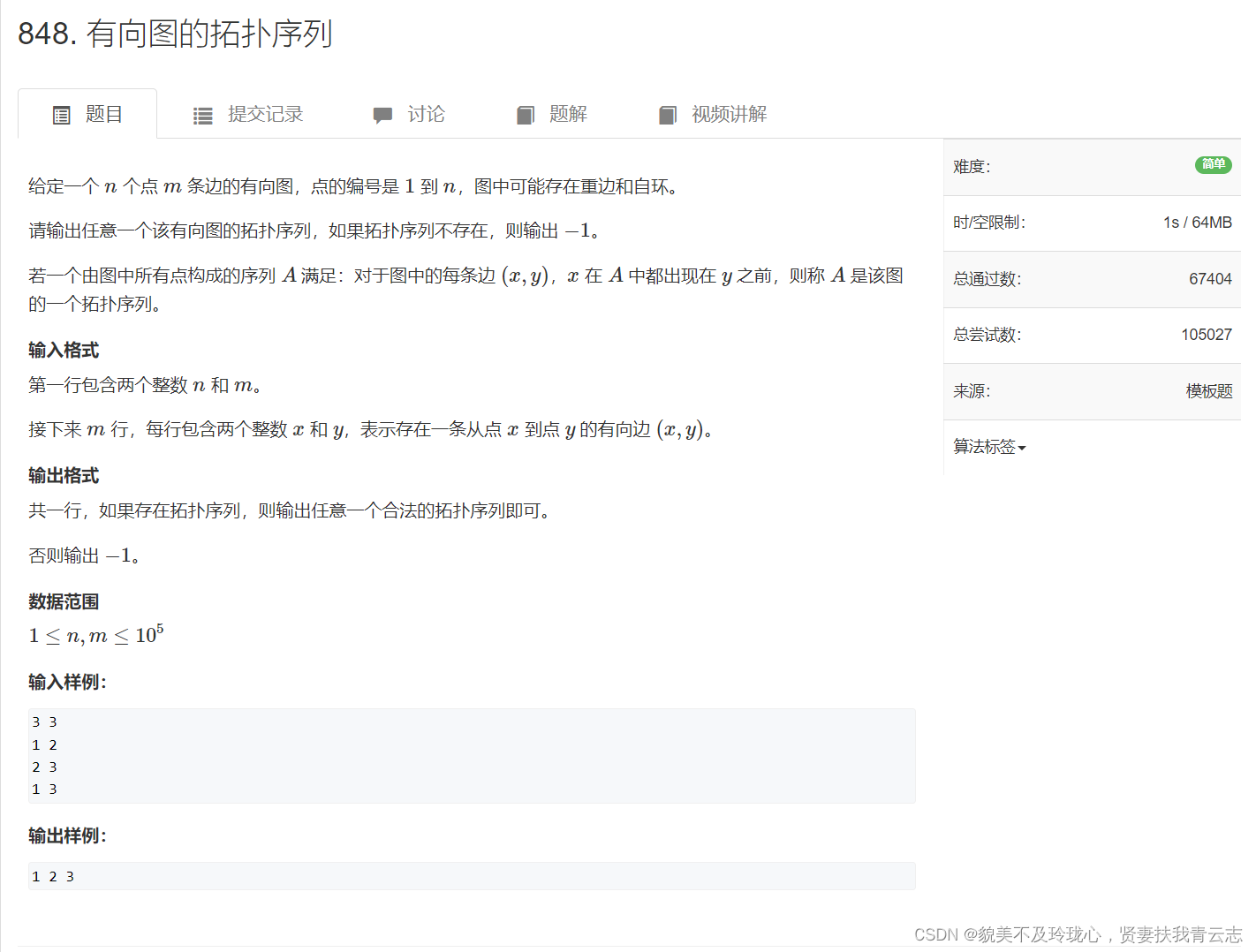
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int q[N], hh = 0, tt = -1;//队列保存入度为0的点,也就是能够输出的点,
int n, m;//保存图的点数和边数
int d[N];保存各个点的入度
//链表存储有向图
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void topsort(){
//把所有的入度为0的点放入队列
for(int i = 1; i <= n; i++){//遍历一遍顶点的入度。
if(d[i] == 0)//如果入度为 0, 则可以入队列
q[++tt] = i;
}
//整个拓扑排序思路是采用每次遍历一个点,就删除一条边,等于入度减1。
//如果这个图是拓扑图,最终结果就是所有点都在队列中
//如果不是拓扑图就会还有一些点还有边。
while(tt >= hh){//循环处理队列中点的
int a = q[hh++];
for(int i = h[a]; i != -1; i = ne[i]){//循环删除 a 发出的边
int b = e[i];//a 有一条边指向b
d[b]--;//删除边后,b的入度减1
if(d[b] == 0)//如果b的入度减为 0,则 b 可以输出,入队列
q[++tt] = b;
}
}
if(tt == n - 1){//如果队列中的点的个数与图中点的个数相同,则可以进行拓扑排序
for(int i = 0; i < n; i++){//队列中保存了所有入度为0的点,依次输出
cout << q[i] << " ";
}
}
else//如果队列中的点的个数与图中点的个数不相同,则可以进行拓扑排序
cout << -1;//输出-1,代表错误
}
int main(){
cin >> n >> m;//保存点的个数和边的个数
memset(h, -1, sizeof h);//初始化邻接矩阵
while (m -- ){//依次读入边
int a, b;
cin >> a >> b;
d[b]++;//顶点b的入度+1
add(a, b);//添加到邻接矩阵
}
topsort();//进行拓扑排序
return 0;
}板子
bool topsort()
{
int hh = 0, tt = -1;
// d[i] 存储点i的入度
for (int i = 1; i <= n; i ++ )
if (!d[i])
q[ ++ tt] = i;
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (-- d[j] == 0)
q[ ++ tt] = j;
}
}
// 如果所有点都入队了,说明存在拓扑序列;否则不存在拓扑序列。
return tt == n - 1;
}
文章来源:https://blog.csdn.net/qq_61553520/article/details/135320525
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 树的运用-计算器
- tempfile模块报错:PermissionError: [Errno 13] Permission denied的解决方法
- 鸟类分类、鸟类声音相关深度学习数据集大合集
- webpack学习-6.缓存
- 虚拟路由器中的Source NAT与Static NAT
- 开发知识点-Weblogic
- RabbitMQ手动应答
- JS中垃圾数据是如何自动回收的
- 政务大数据能力平台建设方案:文件全文30页,附下载
- wpf DataGrid 实现拖拽变换位置,双击拖拽向下自动滚动