二叉树数据结构：深入了解二叉树的概念、特性与结构

在探索栈和队列之后（大家可以移步至我的数据结构专栏）：T-rLN的数据结构专栏

我们转向了更为复杂而有趣的数据结构——二叉树。本文将引领我们进入二叉树的世界，从最基本的概念和结构开始，逐步深入了解二叉树的顺序结构和链式结构

---

---

1.树概念和结构

1.1树的概念

树是一种抽象数据类型（ADT）非线性的数据结构，它由节点组成的集合构成，节点间通过边连接。

它的命名灵感来源于现实生活中的树木结构。类似于自然界中树木的结构，树这一数据结构的视觉表示也呈现出分支延伸的形态，由根部向外延伸出分支，这种分支的结构特点赋予了数据结构树这一名称（一个倒挂的树）

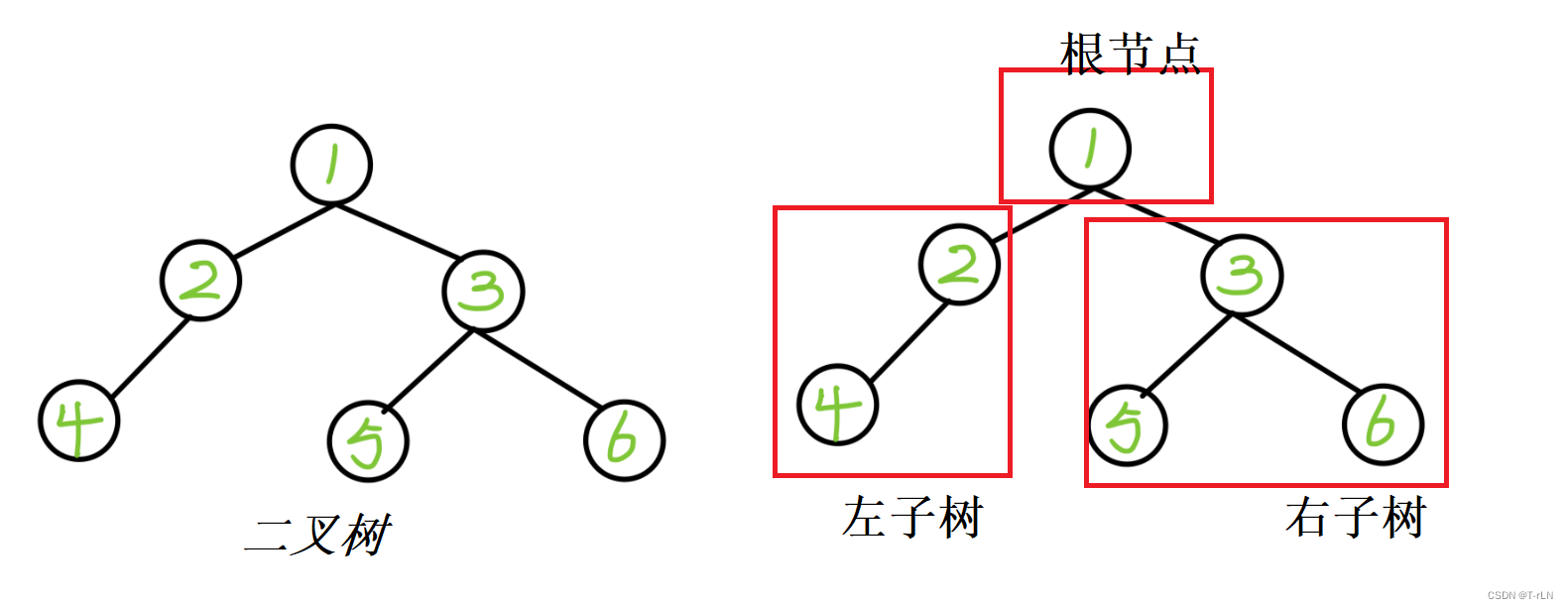
• 树中有一个特殊的节点，称为根节点，它位于树的顶部，没有父节点（前驱节点）
• 树中除根节点外，其他节点都被分成了若干个互不相交的集合，每个集合又形成了一棵类似于树的子树。这里的每个子树都类似于整体的树结构，它们都有一个根节点，这个根节点在当前子树中有且只有一个前驱节点（即父节点），但可以有零个或多个后继节点（子节点）
• 这种定义描述了树这种数据结构的递归性质

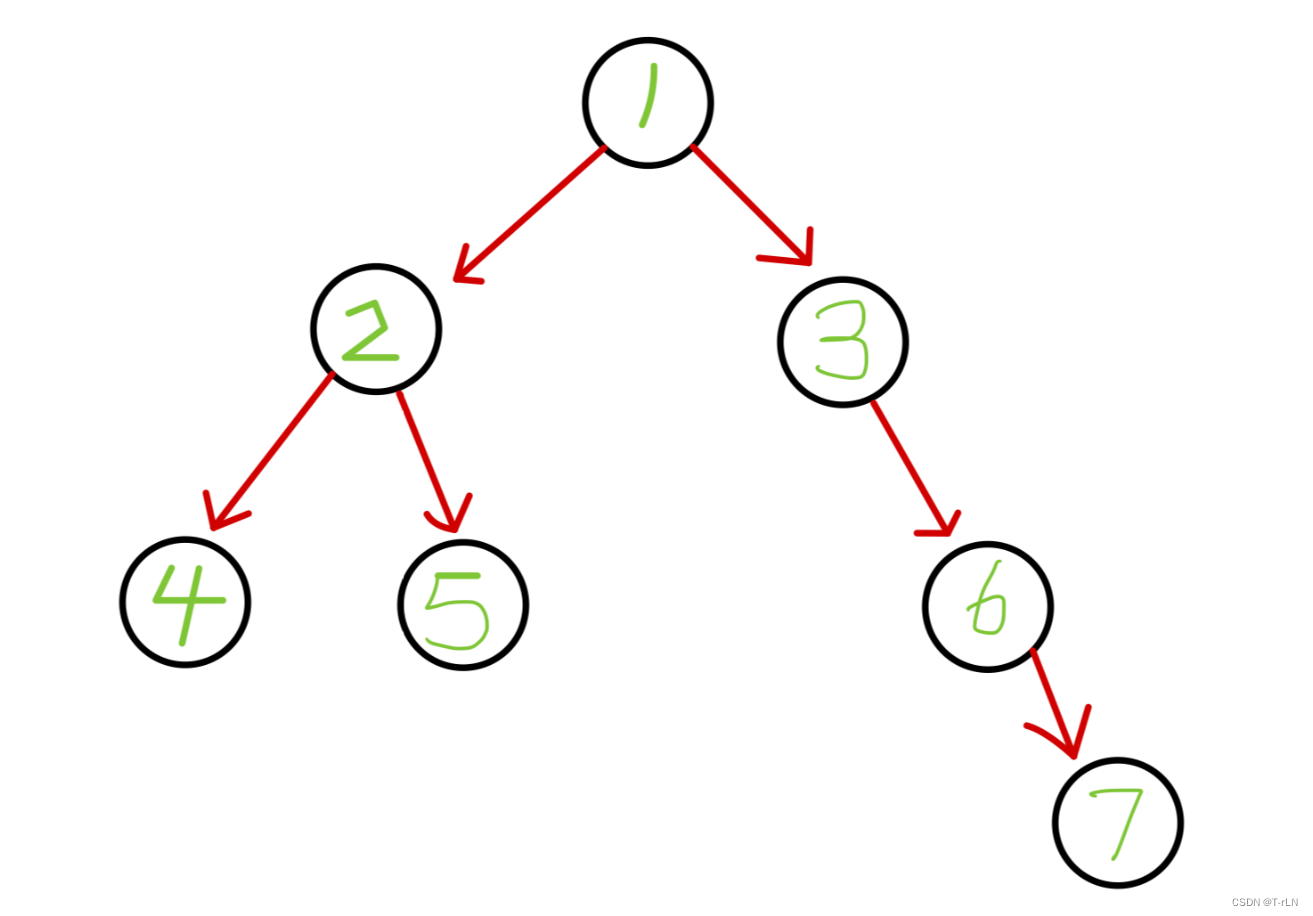
但是要注意：树形结构中，子树之间不能有交集，否则就不是树形结构

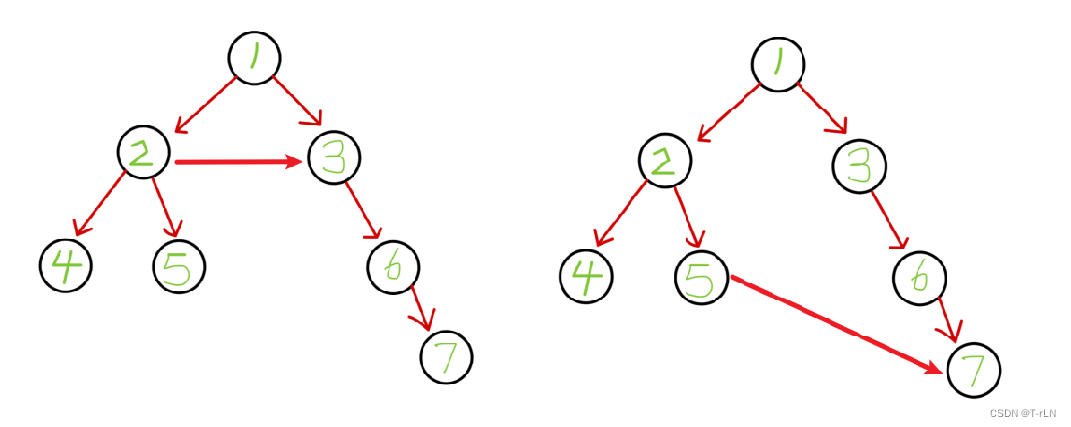
这些都不是树。 树的要求：

• 子树不能相交
• 除了根节点以外，其余节点只有一个父节点
• 一个有哦X个节点的树，边的数量是X-1（梦回离散数学）

1.2树的相关概念

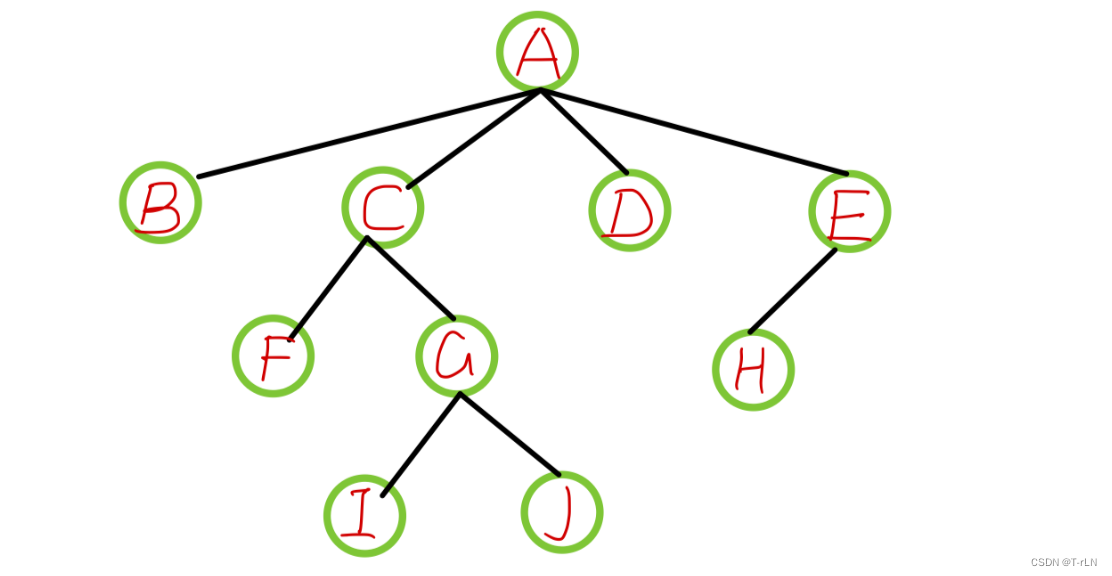
节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A的为4

叶节点或终端节点：度为0的节点称为叶节点； 如上图：B、D、H、I…等节点为叶节点

非终端节点/分支节点：度不为0的节点； 如上图：C、E、G…等节点为分支节点

双亲节点/父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点

孩子节点/子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点

兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点

树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为4

节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推(也有把跟视为第0层的)；

树的高度或深度：树中节点的最大层次； 如上图：树的高度为4

节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先

子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙

森林：多棵互不相交的树的集合称为森林

1.3树的表示

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，既然保存值，也要保存结点和结点之间的关系。实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等

1. 双亲表示法：在每个节点中存储一个指向其父节点的指针或索引

typedef struct {
    int data; // 节点数据
    PTNode* parent; // 指向父节点的指针或索引
} PTNode;

typedef struct {
    PTNode* nodes; // 存储所有节点的数组（要动态的）
    int n; // 树中当前节点数
} PTree;

1. 孩子表示法：每个节点保存一个指向其第一个子节点的指针
2. 孩子兄弟表示法（也叫作左孩子右兄弟表示法）：每个节点有指向其第一个孩子的指针和指向其右兄弟的指针

typedef struct CSNode {
    int data; // 节点数据
    struct CSNode* firstChild; // 指向第一个子节点的指针
    struct CSNode* nextSibling; // 指向右兄弟节点的指针
} CSNode;

1.4树的实际应用

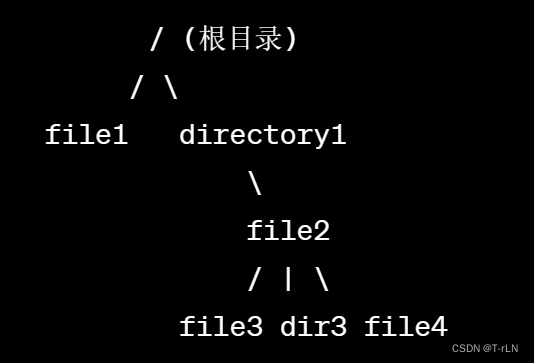
在 Linux 文件系统中，树形结构是文件和目录组织的基础。文件系统以树的形式组织文件和目录，根目录是整个文件系统的顶层，所有的文件和目录都从根目录开始分支。每个目录（包括根目录）都可以包含文件和其他目录

---

2.二叉树概念和结构

2.1二叉树的概念

二叉树是一种重要的树形数据结构，它由节点构成，每个节点最多有两个子节点(不是必须两个)，分别称为左子节点和右子节点。这两个子节点通常称为左子树和右子树

从上图可看出：

• 二叉树不存在度大于2的结点
• 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

2.2两种特殊二叉树

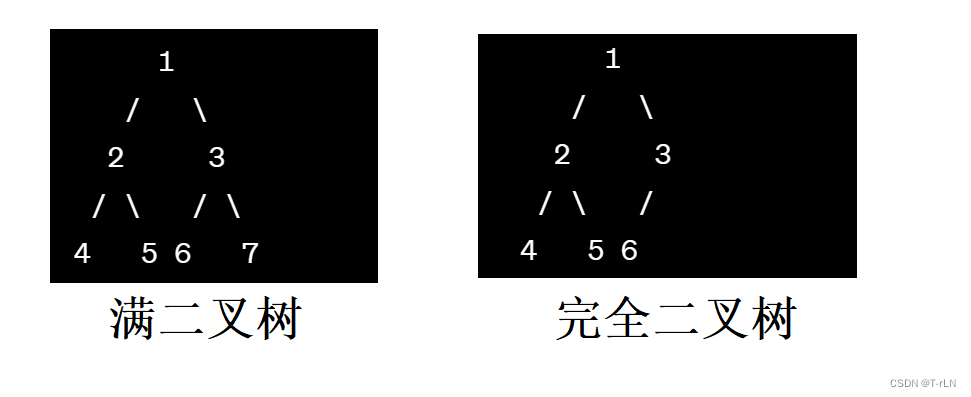
1. 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。换句话说，在满二叉树中每个节点都有两个子节点
2. 完全二叉树：是一种特殊的二叉树，在一棵二叉树中，如果除了最底层，其他层的节点都是满的，并且最底层的节点都从左至右依次填满，这样的树被称为完全二叉树

满二叉树是一种特殊的完全二叉树

2.3二叉树的性质

1. 若规定根节点的层数为1，则一棵非空二叉树的第n层上最多有 $2^{n?1}$个结点(第一层$2^0$，第二层$2^1$);
2. 若规定根节点的层数为1，则**深度为h的二叉树的最大结点数（节点总数）**是：$2^h?1$

• 第一层（根节点层）有 1 个节点。
• 第二层有最多 2 个节点。
• 第三层有最多 4 个节点。
• …
• 第 ? 层有最多 $2^{h?1}$个节点。

? 所以，前 ?h 层的节点数之和为 1+2+4+…+$2^{h?1}$=$2^h?1$

3. 若规定根节点的层数为1，具有n个结点的满二叉树的深度(h):$lo{g}_2(n+1)$

4. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有：

• 若i>0，i位置节点的双亲序号：(i-1)/2 ； i=0，i为根节点编号，无双亲节点
• 若2i+1<n,则左孩子坐标：2i+1；2i+1>=n否则无左孩子
• 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

2.5二叉树的储存结构

1. 顺序储存（数组）：顺序结构存储就是使用数组来存储，一般数组只适合表示完全二叉树，因为不是完全二叉树空间的浪费比较大。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组，在逻辑上（把它想象成，把它看作是）是一颗二叉树
2. 链式储存（链表）：二叉树的链式存储结构是指，用链表来表示一棵二叉树。通常的方法是链表中每个结点由三个域组成，数据域、左指针域和右指针域。左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址，数据域就存储数据

---

这次就到这里啦，下一次大概率是二叉树的顺序结构和堆的相关内容，感谢大家的支持！