代价函数(Cost Function)
代价函数公式
????????为了实现线性回归,第一个关键步骤是定义一个叫做代价函数的东西,成本函数会告诉我们这个模型做的怎么样,以便我们更好的去改进模型。
????????下面是上一篇中用到的例子,我们使用的模型是线性回归模型,w和b叫做参数(parameter),有时候我们也叫它们权重(weight)或者系数(coefficient),在机器学习中,我们可以调整参数来改进模型。

? ? ? ? 在建立一个线性回归模型的时候,我们要做的事情就是找到合适的w和b,从而使得f可以很好的拟合数据,比如下面这样

? ? ? ? 假如我们暂时选择了上面那条直线作为线性回归模型,对于训练集中的第i个训练样本来说,预测得到的值
,那现在的问题就是怎样找到w和b使得大部分的
和
都接近。?

????????要回答上面的问题,我们应该先看一看如何衡量一条线与训练集的拟合程度,为了达到这个小目标,我们得构造一个代价函数(Cost Function) ,代价函数会预测,并且用它减去y,
被叫做误差(error),我们是通过距离来衡量的,所以应该要计算误差的平方
,接下来要将所有的误差整合起来,从1到m对误差进行求和(就不打公式了,不知道为什么csdn打不出这个),求和之后,数据越多代价函数值就越大?这显然不合理,所以我们又给和除以m,最后就是这样

????????但是事实上为了后续计算更加方便,这个代价函数还要除以2,我们也叫它平方误差代价函数,我们做出代价函数是为了找出使代价函数减小的w和b。

? ? ? ? 在机器学习中,不同的人在不同的场景会使用不同的代价函数,但是平方误差代价函数是迄今为止对线性回归最通用的代价函数。
理解代价函数
? ? ? ? 学习了代价函数的数学定义,现在让我们来更直观的看代价函数。来以一个很简单的模型为例:,那么参数为w,代价函数为

????????我们要做的就是找到一个使J最小的w值,下面这个例子中,训练集为(1,1),(2,2),(3,3),当m=1时,我们可以计算得=(1,1),
=(2,2),
=(3,3),那么

? ? ? ? 当w=0.5时,我们可以计算的=(1,0.5),
=(2,1),
=(3,1.5),按照同样的方式计算J(0.5)大约等于0.58
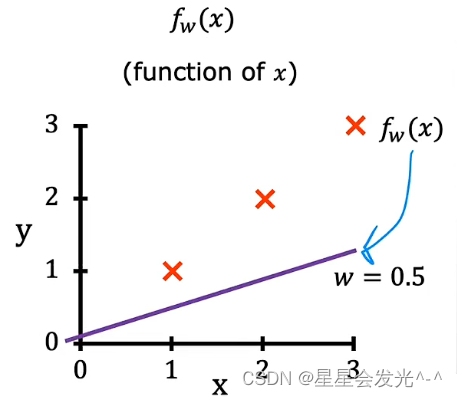
????????当m=0的时候,按照上面的方式算得J(0)约等于2.3
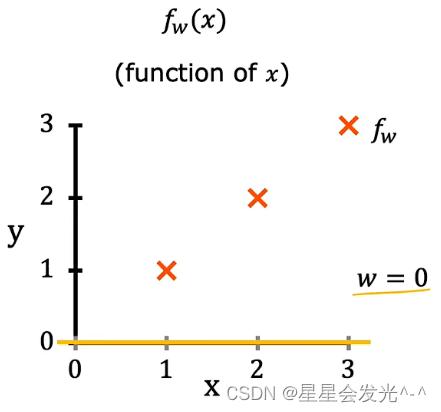
?????????最终我们得到J(w)随m变化得图象是这样的,当然这是一个理想的简化的例子,但是这可以让我们更好的理解代价函数,所以线性回归就是要找到能使J最小的w或者w,b

可视化代价函数
? ? ? ? 上面我们是做了一个简单的例子(b=0),接下来,我们让b不等于0来看看效果,上面是一个二次函数的样子,这里就不难联想到三维应该是类似于一个碗的样子,我们要找一个最好的w和b,就是要找这个“碗”的底。

总结
????????这一篇里我们学了怎么去衡量一个回归模型的好坏,以及怎么通过参数改进模型,应该理解并记住的是代价函数的公式,还有就是知道代价函数大概是长什么的,相信会对后面的学习有所帮助。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Java 基础 - Java 多态性详解与实例解析
- 模型评估:超参数调优
- MyBatis——MyBatis的延迟加载
- 【第三章】数字信号处理 DFS离散傅里叶级数与DFT离散傅里叶变换
- Java期末复习知识点
- c++中构造和析构函数
- Spring Boot使用JUnit和Mockito进行Service层单元测试
- flutter使用shared_preferences依赖库实现简单的本地数据存储,封装成一个简单的单例类,方便前端同学使用
- 【C程序设计】C函数
- vue echarts地图