实时渲染 -- 光追（Ray Tracing)

发布时间：2024年01月24日

光栅化 Or 光线追踪

传统的光栅化方式主要是将每个物体进行光栅化后形成若干个像素，然后每个像素需要计算光源直接照射到自己并反射回眼睛而形成的颜色。这种算法方式是极快的，但是只能表示直接光照，图像质量较低。

Bling-Phong 模型是一个常用于光栅化方式的光照模型，因为光栅化方式本身是极快的，而 Bling-Phong 模型本身也是计算量少的经验公式，因此这两者在低质量渲染中常常相互搭配使用。

而现实的光是复杂的，往往有各种间接光照，而且这种光照的反射次数往往也是不可数的（一个光线可以无数次反弹后最终进入人眼）。因此光栅化方式搭配的光照模型往往是局部（Local）的，不能很好的处理全局（Global）效果，换句话说就是，光栅化的渲染往往仅考虑本物体（一般表现在仅有直接光照），而几乎不考虑其它物体对本物体渲染的影响（一般表现在没有其它间接光照）。

以下场景便是全局（Global）效果的部分现象：

实际上，光栅化中的Environment Mapping/Reflection Mapping是间接光照的特化实现，但是它不可能应用于场景中所有物体（一般只用在那些具有明显镜面反射现象的物体，如镜子、水面）。?

而?光线追踪（Ray Tracing）?则是另一种光照计算的框架方式，有别于传统的光栅化框架方式。

它的主要思路是：因为光路是可逆的，那么就让光线从眼睛出发,沿屏幕每个像素投射出去，判断与场景物体的交点，然后计算该交点的受光照情况。形成一个屏幕图像就需要投射出屏幕分辨率个光线出去，这种计算量无疑是巨大的，但是图像质量极高。

离线渲染（Offline Rendering）就是采取光线追踪框架去实现照片级真实图像，而随着现在硬件的发展，光线追踪逐渐可以被用于实时渲染（Real-Time Rendering），不过仍然需要一些trick去用质量换取速度。

Whitted-Style Ray Tracing

Whitted-Style Ray Tracing：也叫递归式光线追踪（Recursive Ray Tracing），是最经典的光线追踪算法

屏幕上的每一个像素都进行一次光线投射。
光线的每次投射都需要判断交点，而且投射到交点后还可能产生反射、折射，那么就往相应的方向继续进行新的投射，直到投射在漫反射表面（diffuse surface）上。
最后，将每个交点的受光照情况（使用Blinn Phong算法）以一定权重综合起来，得到的颜色即是该像素的颜色。

如下图，光线投射在球上产生了一个交点，并且带有折射和反射，而最后这两个投射都投在了灰色的物体（均为漫发射表面的物体），形成了最后的三个交点（折射了两次，两个交点），接着把这四个交点的受光照情况综合起来就是该像素的颜色。

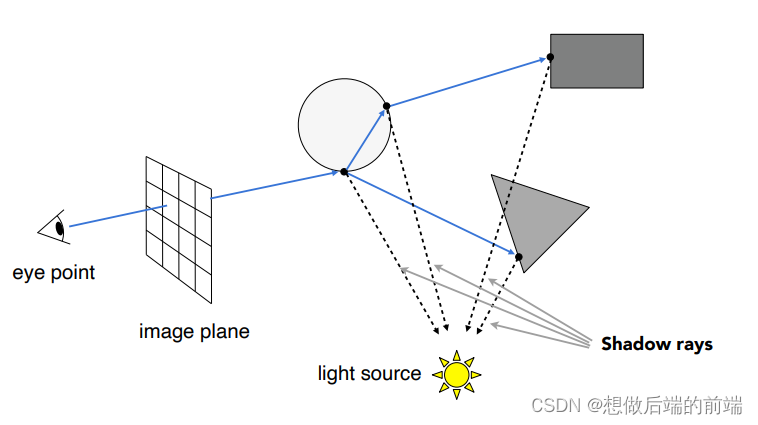
//Whitted-Style Ray Tracing
RayTracing(Point origin,Vector3 direction){
    if(Intersect(origin,direction)){
        hitPoint = GetHitPoint();
        normal = GetHitNormal();
        localColor = BlinnPhongShader(direction,hitpoint,normal,light);
        if(hitPoint is a diffuse sufface)
            return localColor;
        else
            return localColor
                +k1*RayTracing(hitPoint,reflect(direction,normal));
                +k2*RayTracing(hitPoint,refract(direction,normal));
    }
    else{
        return the color of background;
    }
}

需要注意的是：

为了减少递归次数，可以额外给予一定的递归终止条件（如允许的最大反射或折射次数为10）。
光线在每次反射和折射之后都有能量损耗的（由系数决定），因此经过多次投射后的光线贡献的能量就越小。
如果投射光线没有碰撞到物体，一般直接返回一个背景色。
漫反射表面（diffuse surface）是粗糙的表面，可以认为它会向各个方向等强度地反射光，因此光线投射到该表面时，本应该会有无数条光线反射出去，但是为了减少计算量，Whitted-Style 则直接对该交点进行 Blinn Phong 着色后就终止递归。

Whitted-Style Ray Tracing 效果图（Spheres and Checkerboard, T. Whitted, 1979）：

Whitted-Style Ray Tracing 虽然比起光栅化更加正确，但它仍然不算是一个物理正确的算法，这是因为光的传播在物理上不应该是以简单的直线传播，而是以能量的形式往各个方向辐射。

Path Tracing

Path Tracing：是目前最主流的光线追踪算法；相较于 Whitted-Style Ray Tracing 算法，Path Tracing 认为光的传播是以能量的形式向各个方向进行辐射（符合基于物理的渲染），这和渲染方程（Rendering Equation）是一致的：

$L_r(x,w_r) = L_e(x,w_r) + \int _{\Omega ^+}L_{i}(x,w_i)f_r(x,w_i,w_r)(n\cdot w_i)dw_i$

蒙特卡洛方法（Monte Carlo Solution）

那么如何计算这么一个渲染方程的积分？

容易想到使用蒙特卡洛方法：

$L_r(x,w_r)= \int_{\Omega ^+} L_i(x,w_i)f_r(x,w_i,w_r)(n\cdot w_i)dw_i \approx \frac{1}{N}\sum _{i=1}^{N}\frac{L_i(x,w_i)f_r(x,w_i,w_r)(n\cdot w_i)}{p(w_i)}$

还需使用递归的方式解决多次反射的情况：

那么按照淳朴的蒙特卡洛方法，此时光线追踪的基本实现如下：

RayTracing(Point p,Vector3 wr){
    Randomly choose N directions wi~pdf;
    Lr = 0.0;
    for(each wi){
        Trace a ray r(p, wi);
        if(ray r hit the light)
            Lr += (1 / N) * L_i * f_r * cosine / pdf(wi);
        else if(ray r hit an object at q)
            Lr += (1 / N) * RayTracing(q, -wi) * f_r * cosine / pdf(wi)
    }
    return Lr;
}

潜在问题：反弹数很容易爆炸增长（假如?N?取100，最初的一个反射方向将于两次反弹后分化成1,000,000个方向），这种计算量是不可接受的。

那么解决方式是：把?N?? 取1，那么无论多少次反弹，分化的方向最多也只能是1，就不会出现爆炸增长现象。

RayTracing(Point p,Vector3 wr){
    Randomly choose 1 directions wi~pdf(w);
    Lr = 0.0;
    Trace a ray r(p, wi);
    if(ray r hit the light)
        Lr += L_i * f_r * cosine / pdf(wi);
    else if(ray r hit an object at q)
        Lr += RayTracing(q, -wi) * f_r * cosine / pdf(wi);
    return Lr;
}

当然这样做会让蒙特卡洛采样数降低了很多，为了避免出现 noisy，可对同一屏幕像素重复多次Ray Tracing着色。若干次着色后（渲染一定时间后）就可以得到不那么 noisy 的图像了。

俄罗斯轮盘赌（Russian Roulette，RR）

实际上仅使用蒙特卡洛方法还是不够的，Path Tracing的另一个潜在问题是：递归是基本不会停止的，因为总有光路打在光源以外的地方。

一个想法是将递归函数引入反弹次数记录，超过一定次数便强行终止函数。但是这样是不正确的，因为强行终止函数意味着能量的凭空丢失（不守恒），导致渲染画面偏暗。

俄罗斯轮盘赌（Russian Roulette）?的解决方法是：

假如一个 shading 函数理应输出为? $L_r$ ，现在给 shading 函数设置一定概率?P?输出能量? $\frac{L_r}{P}$ ，概率?1?P?输出能量 0： $E = P*(\frac{L_r}{P}) +(1-P)*0 = L_r$

这个函数的输出期望值?E?与理应输出 $L_r$ 相等，也就是说那么只要样本数足够多，这种 shading 将会是能量守恒（无丢失能量）。

RayTracing(Point p,Vector3 wr){
    Manually specify a probability P_RR
    Randomly select ksi in a uniform dist. in [0, 1]
    if(ksi > P_RR)
        return 0.0;

    Randomly choose 1 directions wi~pdf(w);
    Lr = 0.0;
    Trace a ray r(p, wi);
    if(ray r hit the light)
        Lr += L_i * f_r * cosine / pdf(wi);
    else if(ray r hit an object at q)
        Lr += RayTracing(q, -wi) * f_r * cosine / pdf(wi);
    return Lr / P_RR;
}

通过概率?1?P?? 的终止条件，我们便可以避免 Path Tracing 无止尽递归。

光源采样（Sampling the Light）

Path Tracing 里直接光照部分有一个效率问题：ray 打在光源上的概率往往极低（因为光源面积一般相都很小），很容易造成大量的递归运算最终都浪费掉（还没见到光源就被提前终止了）。

为此，聪明的人类转换了采样思路，从对半球上的采样转变成对光源面（假设光源面积=A）上的采样：

本来应该从半球上随机取一个方向投射射线检测是否与光照相交，现在变成了在光源面上随机选一点检测是否能射回到x。

$dw = \frac{dAcos\theta '}{\left \| x'-x \right \|^2}$

那么直接光照（注意不是间接光照）的渲染方程将会是：

$L_r(x,w_r) = \int _{\Omega ^+}L_i(x,w_i)f_r(x,w_i,w_r)cos\theta dw_i = \int _A L_i(x,w_i)f_r(x,w_i,w_r)\frac{cos\theta cos\theta '}{\left \| x'-x \right \|^2}dA \approx \frac{1}{N}\sum _{i=1}^N(\frac{L_i(x,w_i)f_r(x,w_i,w_r)}{p(x')}\cdot \frac{cos\theta cos\theta '}{\left \| x'-x \right \|^2})$

其中，N=1。

这样在计算直接光照时，原本一个半球上的积分转变成一个光源面上的积分，这使得 Path Tracing 可以更容易得到直接光照的结果（ray 更容易打在光源），当然贡献的光量也会根据概率调整（概率从原本的1/2pi变成1/A）。

不过还要额外注意直接光照被直接遮挡的情况，一个简易的解决方法是：让 shading point 往光源点投射一条射线，如果没有被遮挡，则计算直接光照并贡献到结果中。

Path Tracing 最终伪代码：

RayTracing(Point p,Vector3 wr){
    // Contribution from the light source.
    L_dir = 0.0;
    Uniformly sample the light at x’ (pdf_light = 1 / A);
    Shoot a ray from p to x’;
    if(the ray is not blocked in the middle)
        L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light ;
	
    // Contribution from other reflectors.
    L_indir = 0.0;
    Test Russian Roulette with probability P_RR;
    Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi);
    Trace a ray r(p, wi);
    if(ray r hit a non-emitting object at q)
        L_indir = RayTracing(q, -wi) * f_r * cos θ / pdf_hemi / P_RR;
    
    return L_dir + L_indir;
}

加速射线相交检测（by 空间数据结构方法）

可以看到上述两种光线追踪算法都需要大量使用射线相交检测，因此射线相交检测算法的快慢对整个光追算法的影响很大。一个思路是，使用空间数据结构去加速射线相交检测。

Nvidia的RTX系列显卡为了支持实时光追，还特地设计了专用于加速射线相交检测运算的硬件，这使得实时光追成为可能。

使用Grid

基本步骤：

先将每个物体所占据位置对应的网格填入物体索引信息。
射线通过按方向递进的方式遍历网格，若遍历时发现网格存在物体，则再与具体物体进行相交检测。

Grid的划分格子数是一个重要的考量。当格子数过少时，会退化成几乎无加速（都在同一个格子）的效果；当格子数过多时，射线遍历的网格数会变得过多，导致计算更缓慢（甚至负优化）。Grid在物体分布较均匀的场景（如草地）中可以较好的运行优化效果，但在一般性的场景（物体分布不均）中往往不尽人意。

使用K-D Tree

k-d树轮流使用不同的维度去划分，并且每次划分都通过一个标量去表示在当前维度的某个值作为划分界线。

基本步骤：

对场景构造k-d树
从k-d树根节点（作为父节点）开始，对父结点进行射线-AABB相交检测（即检测射线是否穿过AABB区域）：
- 若与AABB相交，则对两个子结点分别做射线-AABB相交检测。
- 若不相交，则停止本次检测。

k-d树的结构是不支持随物体变化而动态变化的，每次发生变化必须得重新进行构造，也就是说只适用于静态物体。当然保持相同的划分，只让变化的物体注册进相应的划分区域也是可行的，然而这样可能导致k-d树的结点物体分布不均匀，还不如使用Grid来表示让计算更加简单。

使用BVH

基本步骤：

对场景的所有三角形构造BVH树（示例使用的Bounding Volume是AABB包围盒）
从BVH树根节点（作为父节点）开始，进行射线-包围盒检测（即检测射线是否穿过父包围盒）：
- 若与父包围盒相交，则对两个子包围盒分别做射线检测。
- 若不相交，则停止本次检测。

Intersect(Ray ray, BVH node){
    if(ray misses node.bbox){
        return;
    }

    if(node is a leaf node){
        test intersection with all objs;
        return closest intersection;
    }
    
    hit1 = Intersect(ray, node.child1);
    hit2 = Intersect(ray, node.child2);

    return the closer of hit1,hit2;
}

BVH树的结构是可以随物体变化而动态变化的（有一定开销）。而且相比区域划分，基于对象的划分可以让包围盒更加紧凑，也就是说对包围盒检测更加更加贴近于对实际所占空间（包围盒内所有物体的总和）的检测，因而可以减少所需的检测层数。

总结

现实光照=直接光照+反弹1次的间接光照+反弹2次的光照+...现实光照=直接光照+反弹1次的间接光照+反弹2次的光照+...

光线追踪（Ray Tracing）通过递归的方式实现了间接光的效果（递归多少次意味着反射了多少次），因此在使用光线追踪算法的时候其实就相当于间接实现了全局光照（Global Illumination）的效果，这也是光线追踪的一个明显优点。

光线追踪框架下的两种主要算法：

Whitted-Style Ray Tracing：基于光照是光线直射的理念。
Path Tracing：基于光照是能量辐射的理念，使用蒙特卡洛方法（Monte Carlo Solution）+ 俄罗斯轮盘赌（Russian Roulette，RR）+ 直接光照使用光源采样方式。

其中，Path Tracing 是最常见的 Ray Tracing 算法，因为它几乎达到100%的正确，拥有 Photo-Realistic级别的图像质量。不过这里只是点了它的基本面貌，它仍然还有很多改进的地方（例如重要性采样）没有讲到。此外，为了达成实时渲染的性能，更是需要很多工作要做。

文章来源:https://blog.csdn.net/gghhb12/article/details/135822839
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！