二维变换与直线的裁剪和多变形的裁剪

首先我们先来推导旋转变换的公式，对于平面内的一点（x,y）如下图所示，将其逆时针旋转θ角至（x1,y1）应该会发生什么？

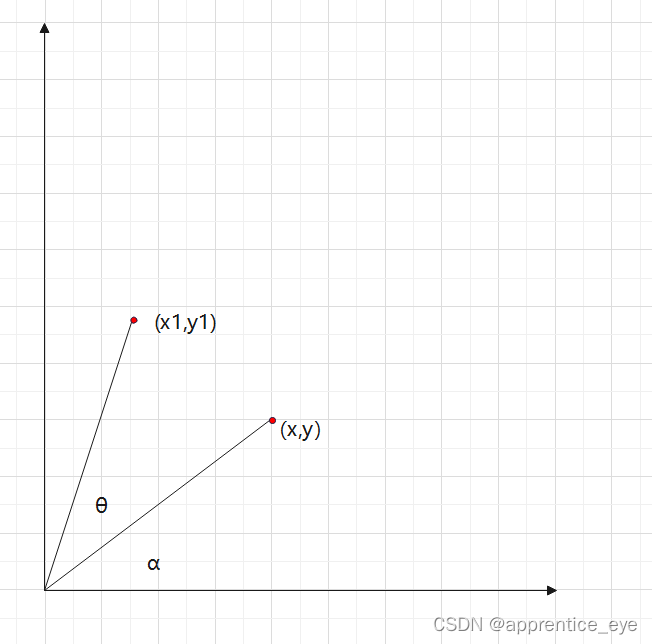
我们假设（x,y）点与原点所连直线与x轴的夹角为α，旋转θ角之后到了(x1,y1)点，此点与原点所连直线与x轴的夹角为(α+θ)，我们可以写出下面两个方程组对于点（x,y）

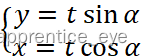
对于（x1, y1）则可以写出下式：

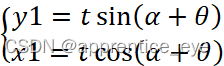
进一步得：

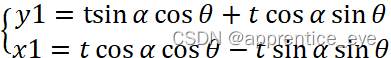
将（x,y）的方程代入(x1,y1)的方程可以得到下面的式子：

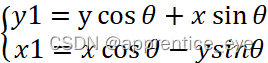
转化称为矩阵运算如下：

这样我们就得到了按照逆时针旋转θ角的公式变换的公式，而顺时针进行旋转θ角相当于逆时针旋转-θ角，公式可以变换为

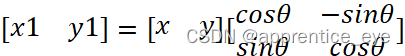
?? 这样我们就知道如何进行旋转变换了，接下来我们看一下平移变换是怎么做的

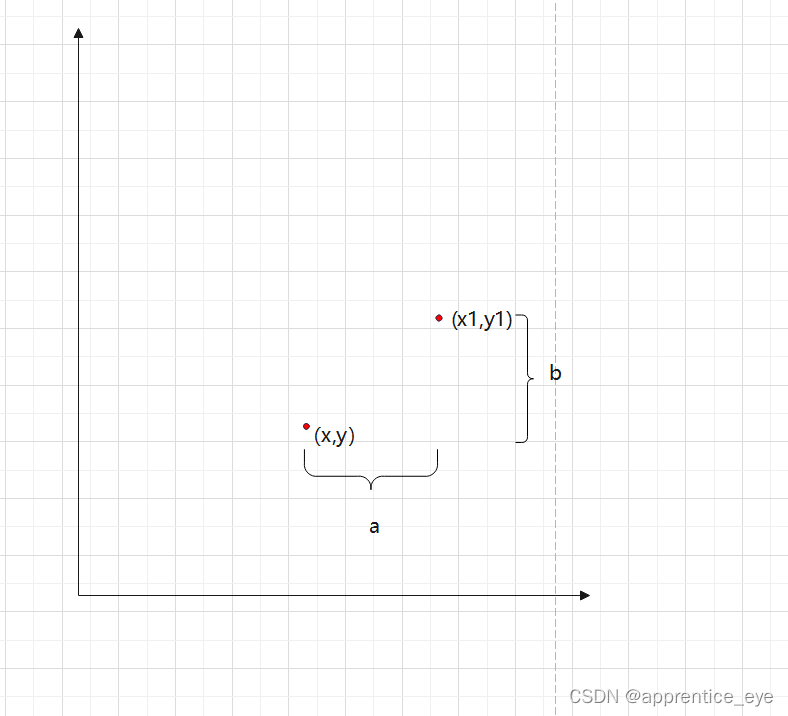
可以看出

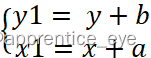
则写为矩阵的形式为：

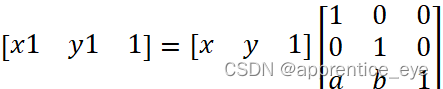
我们可以发现此矩阵的形式是可以容纳刚才的旋转变换的矩阵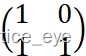可以看作旋转角度为0的旋转变换下方的[a? b]则表示平移变换。

如何进行比例变换呢？

此时存在下列关系

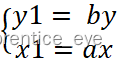
转换成矩阵运算：

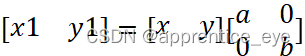
这样可以进行比例变换。

我们可以看出这些变换是可以在一个矩阵中表示出来的

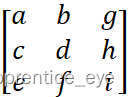
我们可以知道a、b、c、d与旋转变换和比例变换有关，e、f与平移变换有关

其中i与整体比例变换有关，我们可以从下式看出

?

只有在中i为1时，前面的才表示坐标的话，等价于可以看出当i>1，x与y被等比例缩小了，i<1时，x与y被等比例放大了，这就是等比例变换。

而g、h会使得整体的变换除了与i有关还会与初始的x与y有关，其中若i为0，则缩放会与x和y相关。

有了这些我们就能够实现坐标的变换了，而且可以通过组合变换矩阵完成复杂的变换。

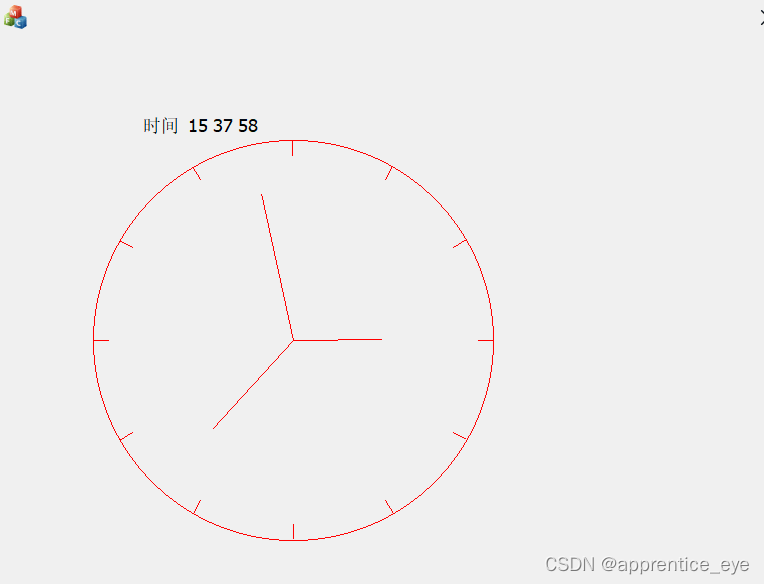
结合之前实现的直线的扫描转换与圆的扫描转换等算法我们就可以实现一些简单的变换效果，如通过组合变换实现简陋的动态时钟：

实现的思路，通过获取当前的时间可以确定当前时间应该在的位置，通过变换可以将时间值转换为角度值，此角度代表了与指向十二点时表针的夹角，转换之后，我们所要实现的就是将表针从十二点整移动到指定的位置，接下来我们就可以移动表针，移动表针可以采用矩阵的方式，因为矩阵比较小，旋转变换2*2矩阵就够了，所以我们直接求出旋转后的位置即可，然后绘制表针，通过不停的获取时间刷新表针就可以实现动态的效果了。

效果图（注：因为动图不适合加在word文档中，所以只截取其中两幅在不同位置的时间）如下：

接下来我们就来看一下直线与多边形区域的裁剪：

直线的裁剪是较为简单的一种情况，我们可以通过对多边形的区域进行编码，整个区域就会被分成下面的的几个部分

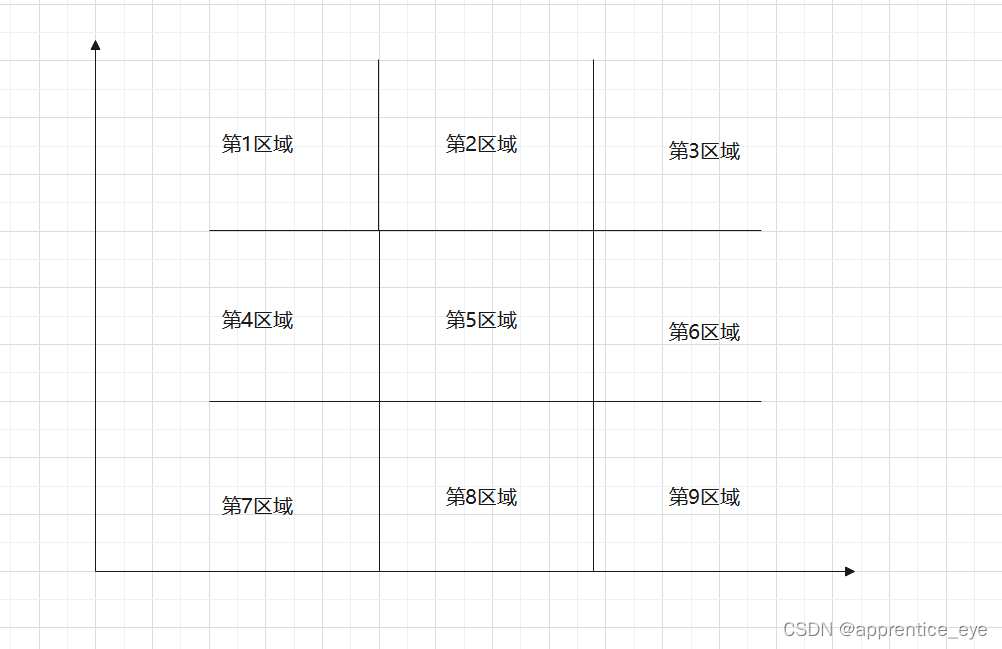
九个区域共有九种状态。四位二进制编码就可以表示所有的状态，对于编码我们可以使用第一位为1表示位于上边界的上面，为0表示位于上边界的下面，第二位为1表示位于下边界的下面，为0表示位于下边界的上面，第三位为1表示位于右边界的右边，为0表示位于右边界的左边，第四位为1表示位于左边界的左边，为0表示位于左边界的右边，由此这九个区域的编码可以写成下面的：

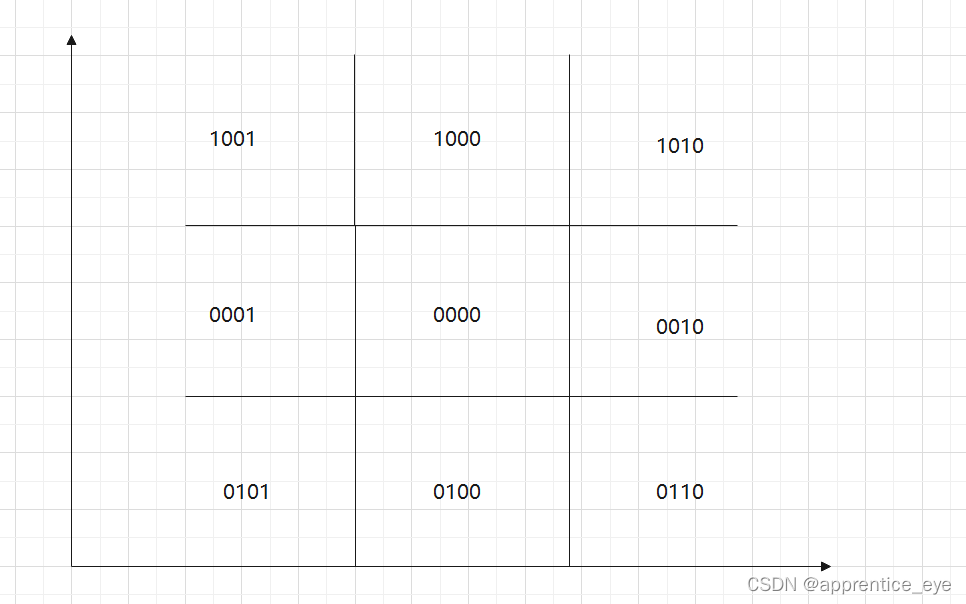
接下来我们就来讨论一下要保留哪些直线，完全保留的显然要两个端点都在0000区域内，即下面的情况

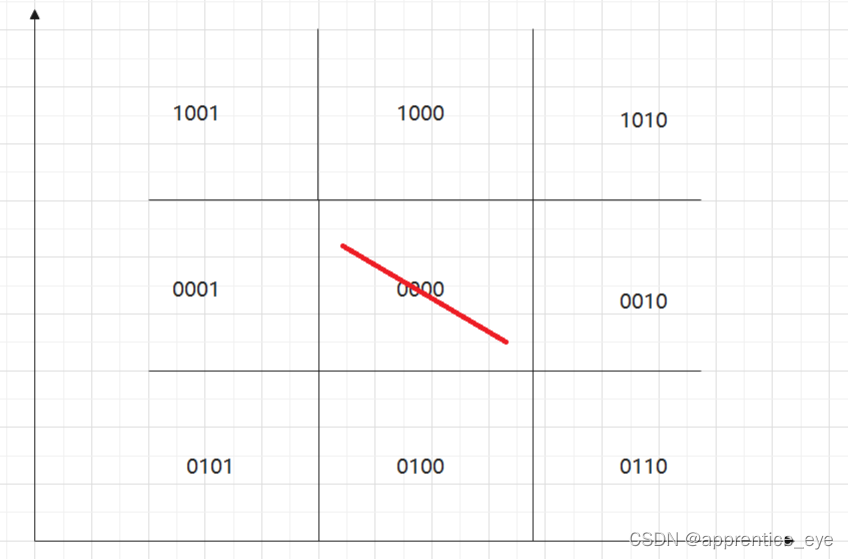
完全抛弃的直线段显然是两个点都位于一条边界的外侧，而都位于一个边界的外侧必然那一位都为1，其他位情况不用看，而这两位都为1必然意味着按位进行与运算至少会有一位不为0，即按位与的结果不为零是将直线完全抛弃的条件。

像下面这种直线就是一定要抛弃的。

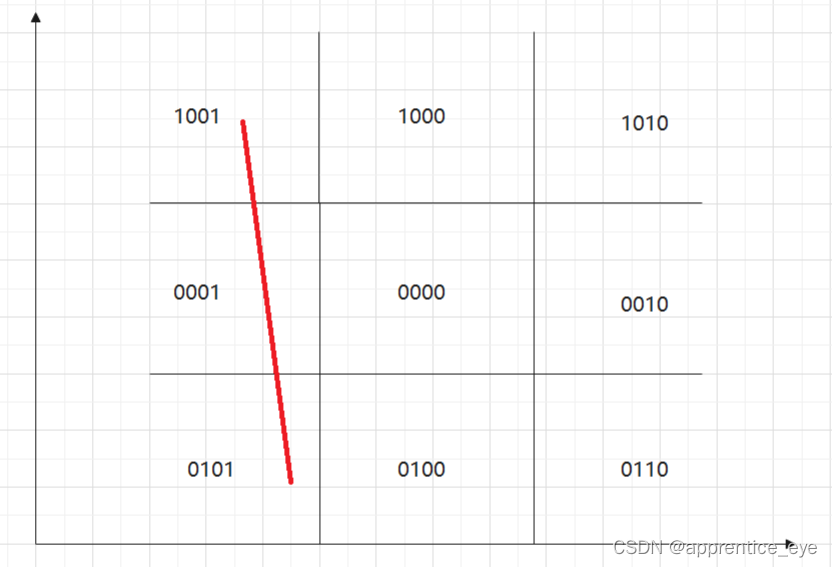
但是还是存在一些情况我们不知道是否完全抛弃，也不知道要保留哪一部分，如何进行取舍呢？下面这种情况就 无法凭借端点所在区域编码的与或运算进行取舍。

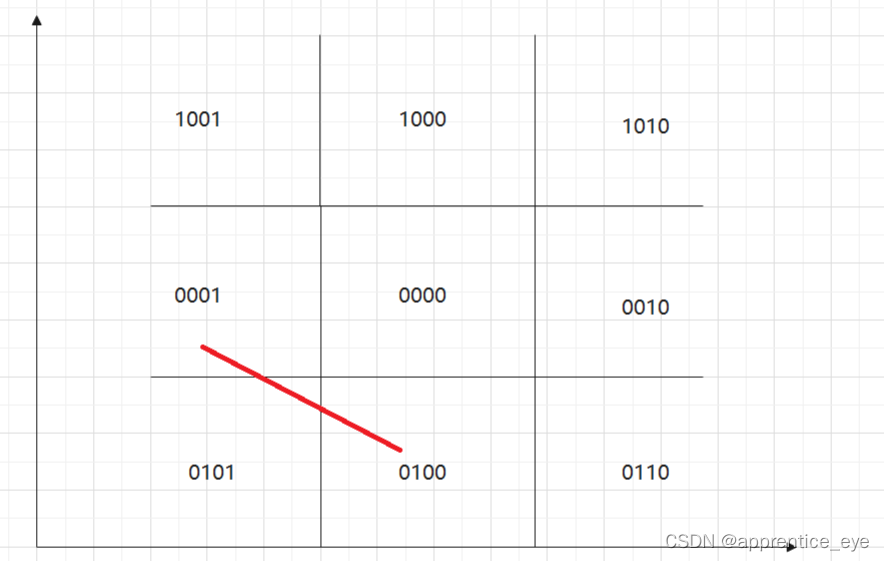
但是这一种无所谓有没有交点了，我们将直线先与边界求交点必然能够得到一点坐标，而刚才求交点的哪一点必然舍弃而新交的交点与没有使用的那一点会组成一个新的直线，再用新的直线段取进行上述判断，最后必然要么这段线段被完全舍弃，要么这段线段中应该保留的部分被保留，显然上述的操作是递归的，我们有了这种思路就可以实现直线的裁减了。

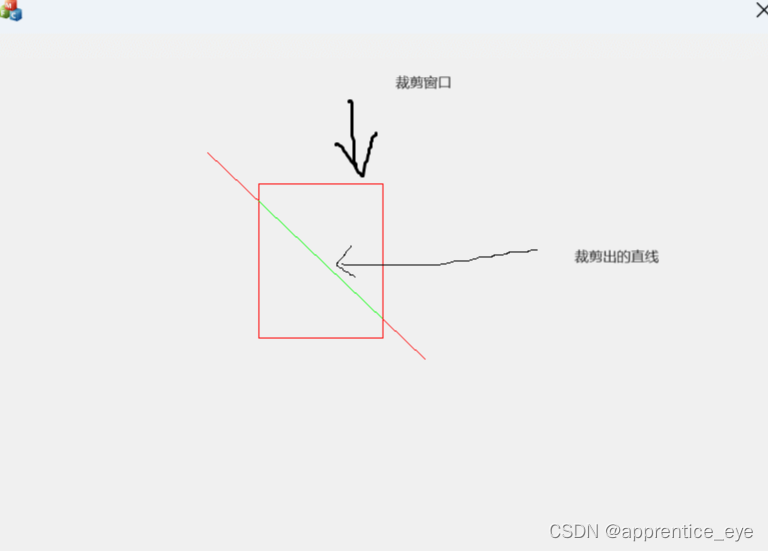
演示效果：

注：动图可能会无法演示，所以只上传将直线截取完成后的截图

多边形的裁剪这一篇文章在我的这一篇文章中那个已经介绍过，附上链接多边形的裁剪：一种基于有效边表的有效多边形裁剪算法的分析?

如果有什么地方讲的不好或者讲错的地方欢迎大家指出来，如果我所讲的对你们有帮助不要忘了点赞、收藏、关注哦!

?我是你们的好伙伴apprentice_eye 一个致力于让知识变的易懂的博主。