降低方差的统计方差(其二):重要抽样法

发布时间：2024年01月02日

§1.问题引入

速成看§2.1,§3,本文中的生成随机数均为独立生成

重要抽样法和平均值估计法有着非常密切的联系,可以说平均值估计法是重要抽样法的一种特殊情况,下面我们通过一个例子来引入重要抽样法

假设我们要通过平均值估计法来估计一个定积分,图像如下

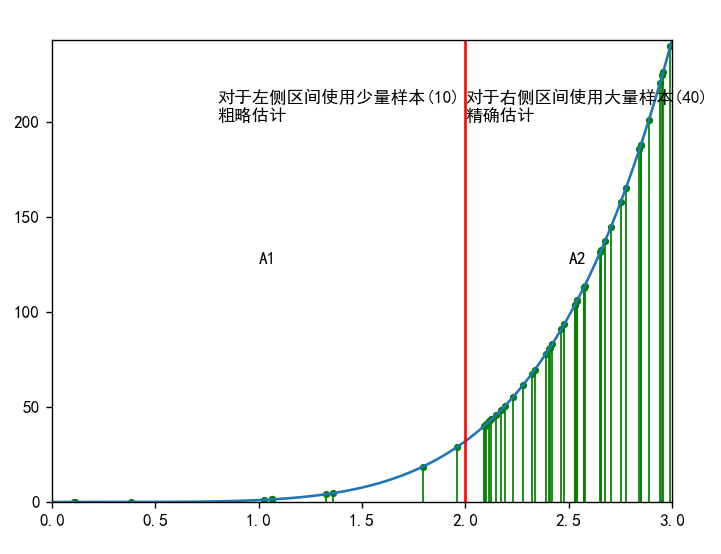
会在A1,A2区域等概率的生成随机数,但是A2区域的值比A1区域的值要大,占主要部分,如果我们将更多的点用来估计A2,减小A2的误差,A1的点虽然变少了,但是由于A1本身比较小,用较少的点估计并不会相差很大,这样是不是能降低方差呢?

也可以参考以下文章的§3.2

写文章-CSDN创作中心

§2.重抽样法的详细介绍

§2.1重抽样法基本步骤

§2.1.1基本步骤

对于积分 $\int_{a}^{b}f(x)dx$

1.选取适当的权因子1/g(X)

2.生成概率密度函数为g(X)的随机变量Y? (注意:g(X)是一个密度函数)

3.计算表达式 $\frac{f(Y_1)}{g(Y_1)},\frac{f(Y_2)}{g(Y_2)}....\frac{f(Y_n)}{g(Y_n)}$ ,求均值即为积分 $\int_{a}^{b}f(x)dx$ 的估计

§2.1.2函数g(Y)的选取

对于权因子的选择,g(X)一般选择与积分函数f(x)形状相似的函数,或者是f(x)的泰勒展开函数,要保证随机变量Y能够得到,且为概率密度函数

可以参考第3节的例子

§2.2无偏性方差减小证明(样本量为n)

§2.2.1对于无偏性

对积分做如下变换

$\int_{a}^{b}f(x)dx=\int_{a}^{b}\frac{f(x)}{g(x)}g(x)dx=E(\frac{f(Y)}{g(Y)})\\ Y\sim g(x)$

可以知道积分值 $\int_{a}^{b}f(x)dx$ 就是随机变量 $\frac{f(Y)}{g(Y)}$ 的平均值

§2.2.2对于方差减小的证明

令 $I$ 为所求积分值? $I=\int_{a}^{b}f(x)dx$

$Var(\widehat{I_1})=\frac{1}{n}Var(\sum_{i=1}^{n}\frac{f(Y_i)}{g(Y_i)})=\frac{1}{n}Var(\frac{f(Y)}{g(Y)})=\\ \frac{1}{n}\int_{a}^{b}(\frac{f(y)}{g(y)}-I)^2g(y)dy=\frac{1}{n}(\int_{a}^{b}\frac{f^2(y)}{g(y)}dy-I^2)$ ? ? ? ? 2.2.2式

可以看到方差的表达式子,方差的大小由g(y)所决定,当g(y)==1时,Y就是均匀分布,就是平均值估计法,方差和平均值估计的方差一样,回顾上一节求得的平均值估计的方差为 $\frac{1}{n}\left \{ E(f^2(R))(b-a)^2-I^2 \right \}$

同时我们知道,如果g(x)选取不当可能会适得其反,由问题引入的原理我们可以猜到,g(x)和f(x)的形状相似时候(f(x)大时,g(x)就大,生成这个区间的随机数的概率就大)

g(x)选取原理解释

假设 $\frac{f^2(y)}{g^2(y)}==I^2$ 带入式2.2.2得到, $Var(\widehat{I}_1)=0$ ,假设f(x)>0,得到 $g(x)=If(x)$ , $I$ 为常数,所以可以看出当g(x)和f(x)形状越相同时,方差会越小

读者通过观察不难发现,重抽样法将积分 $\int_{a}^{b}f(x)dx$ 转化为积分 $\int_{a}^{b}\frac{f(x)}{g(x)}g(x)dx$ ,从对f(x)的均匀投点,转化为了对f(x)/g(x)图像上的非均匀投点,切f(x)/g(x)会更加平缓,故估计的值会更加的准确

注意:最好不要使用近似抽样法来生成g(x)的随机数,会导致结果不收敛到准确?

§3.重抽样法的应用(样本量为1000)

§3.1

§3.1.1例题分析

估计定积分,准确值为1.718282

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? $\int_{0}^{1}e^{x}dx$

我们不妨选取 $e^{x}$ 的泰勒展开式,展开到一阶为:1+x,将其化成密度函数g(x)=2/3(1+x)

套用§2.1.1中的步骤,基本步骤如下

§3.1.2解题步骤

1.选取g(x)=2/3(1+x)

2.用逆变换法产生Y~g(X)的随机数,Y=(3U+1)^0.5-1其中U是[0,1]上的均匀分布

3计算表达式 $\frac{f(Y_1)}{g(Y_1)},\frac{f(Y_2)}{g(Y_2)}....\frac{f(Y_n)}{g(Y_n)}$ ,求均值即为积分 $\int_{a}^{b}f(x)dx$ 的估计

§3.1.3代码实现

代码演示,并与平均值估计法做比较

####定义g(x)和f(x),重要抽样法
set.seed(1)
g=function(x){
    return=2/3*(1+x)
}
f=function(x){
    return=exp(x)
}
n=1000
m=100
re=NULL     #用来保存每1000次的估计值
for(j in 1:m){
    U=runif(n)
    Y=(3*U+1)^0.5-1     #逆变换法产生分布为g(x)的随机数
    re[j]=mean(f(Y)/g(Y))
}
mean(re)
var(re)

########平均值估计
n=1000
m=100
re=NULL     #用来保存每1000次的估计值
for(j in 1:m){
    U=runif(n)
    re[j]=mean(f(U))
}
mean(re)
var(re)

python:?

import numpy as np
import matplotlib as plt
#重要抽样法
np.random.seed(1)
def g(x):
    return 2/3*(1+x)
def f(x):
    return np.exp(x)
n=1000
m=100
re=[]
for _ in range(1,m+1):
    U=np.random.uniform(0,1,n)
    Y=(3*U+1)**0.5-1
    re.append(np.mean(f(Y)/g(Y)))
print(f"重要抽样法估计值{np.mean(re)},方差:{np.var(re)}")

#平均值估计法
n=1000
m=100
re=[]
for _ in range(1,m+1):
    U=np.random.uniform(0,1,n)
    re.append(np.mean(f(U)))
print(f"平均值估计法估计值{np.mean(re)},方差:{np.var(re)}")

?§3.1.4结果分析

?得到的结果为:

?<-重抽样法? ? ? ? ? ? ? ?? ? ? ? ? 平均值估计法->? ? ?

??

可以看到,重要抽样法的方差更小,结果更加可靠,虽然平均值估计法的结果更加接近准确值1.71828,但这是偶然的,如果实验多次,重要抽样法必然更加可信如下n=1000,我们重复10次,把每次的估计值记录下来进行比较

?显然重要抽样法更加可信,如果将n取值很大,对于这题而言那么重要抽样法结果将于平均值差不多,正如原理所述,投点足够多时,每一个积分区域都可以得到充分的估计,重要抽样法的优势会相对减弱.

下面来看一个更加明显的例子

§3.2

§3.2.1例题分析

估计定积分β(1/2,1/2),精确到小数点后三位,准确值为 $\pi$

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $\beta(\frac{1}{2},\frac{1}{2})=\int_{0}^{1}x^{-0.5}(1-x)^{-0.5}dx$

g(x)的选取?

先观察β(1/2,1/2)中积分函数的图像?

? ? ? ? ? ? ? ? ? ??

错误选取? $((x-0.5)^{6}+0.005)$

函数关于0.5对称,我们要找到一个与此函数形状相似的图形,很容易想到g(x)=(x-0.5)^2或者更高偶数次,如函数 $((x-0.5)^{6}+0.005)$ 与f(x)形状及为相似,归一化后图像为

? ? ? ? ? ? ? ? ? ??

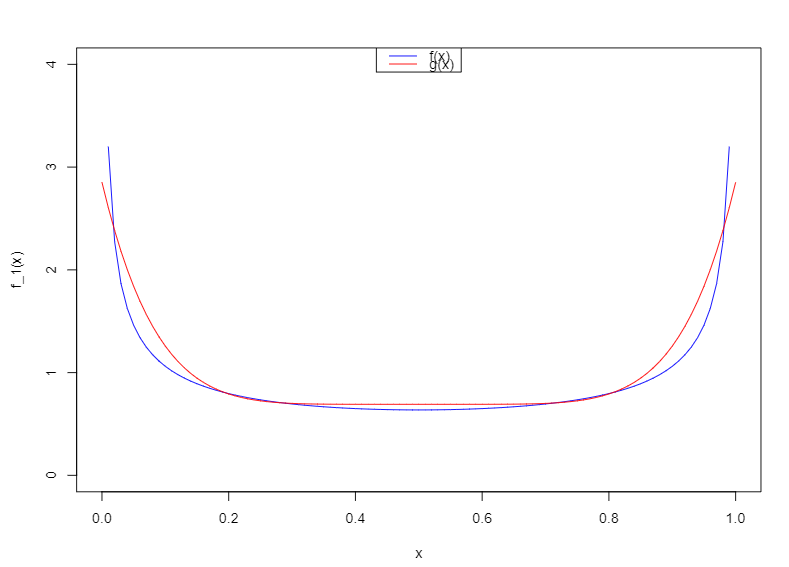
但是服从密度函数为 $((x-0.5)^{6}+0.005)$ 的随机变量,如果采用近似抽样法,会导致结果估计为有偏估计,故不采用

事实上,就算近似区间的划分取1/10000,最终的结果也只收敛到3.10

正确选取

由于f(x)关于x=0.5对称,0.5到0.8十分平缓

我们对右边进行估计,分段选取如下函数(归一化后的g(x))

? ? ? ? ? ? ? ? ? ? ? ?? $g(x)=\left\{ \begin{array}{lr} 1 & 0.5\leqslant x < 0.8 \\ 25*x-19, & 0.8\leqslant x < 1 \\ \end{array} \right.$

?对于概率密度函数为g(x)的随机数,采用复合抽样法,其中p1=0.3,p2=0.7

§3.2.2 基本步骤

基本步骤:

1.选取 $g(x)=\left\{ \begin{array}{lr} 1 & 0.5\leqslant x < 0.8 \\ 25*x-19, & 0.8\leqslant x < 1 \\ \end{array} \right.$

2.生成g(x)的随机数Y? ? #由于篇幅限值,且生成方法不属于本节内容,省略,具体可以看代码实现

3计算表达式 $\frac{f(Y_1)}{g(Y_1)},\frac{f(Y_2)}{g(Y_2)}....\frac{f(Y_n)}{g(Y_n)}$ ,求均值即为积分 $\int_{a}^{b}f(x)dx$ 的估计

?§3.2.3?代码实现


###############重要抽样法
set.seed(1)
#定义函数
f=function(x){
    return=x^-0.5*(1-x)^-0.5
}
g=function(x){
    if(x>=0.8){
        return=(12.5*x-9.5)*2
    }else {
       return=1
    }
}


n=1000
m=100
re=NULL
η=NULL
for(j in 1:m){
    for(i in 1:n){
        R=runif(1)   #复合抽样法,选定抽取哪一部分的随机数
        if(R<=0.3){
            Y=runif(1,0.5,0.8)
        }else{
            U=runif(1)
            a=125/7
            b=-190/7
            c=-((0.8^2)*a+b*0.8)-U
            Y=(-b+sqrt(b^2-4*a*c))/(2*a)   #使用逆变换法抽样
        }
        η[i]=f(Y)/g(Y)
    }
    re[j]=mean(η)
}
mean(re)*2     #最终结果*2
var(re*2)

#######平均值估计法
re=c(0)
for (i in 1:m){
    U=runif(n)
    re[i]=mean(f(U))
}
mean(re)
var(re)

python:

import numpy as np
import matplotlib as plt
#重要抽样法
np.random.seed(1)
def f(x):
    return (x**-0.5)*(1-x)**-0.5
def g(x):
    if x>=0.8:
        return (12.5*x-9.5)*2
    else:
        return 1
    
n=1000
m=100
re=[]
η=[]
for j in range(1,m+1):
    η=[]
    for i in range(1,n+1):
        R=np.random.uniform(0,1,1)   #复合抽样法进行随机数的生成判断
        if R<=0.3:
            Y=np.random.uniform(0.5,0.8,1)
        else:
            U=np.random.uniform(0,1,1)
            a=125/7
            b=-190/7
            c=-0.8*0.8*a-b*0.8-U
            Y=(-b+np.sqrt(b**2-4*a*c))/(2*a)   #采用逆变换抽样法
        η.append(f(Y)/g(Y))
    re.append(np.mean(η))
print(f"重抽样法的估计值{np.mean(re)*2},方差{np.var(re)*4}")  #注意不能直接乘re,re为列表


import numpy as np
import matplotlib as plt
#重要抽样法
np.random.seed(1)
def f(x):
    return (x**-0.5)*(1-x)**-0.5
def g(x):
    if x>=0.8:
        return (12.5*x-9.5)*2
    else:
        return 1
    
n=1000
m=100
re=[]
η=[]
for j in range(1,m+1):
    η=[]
    for i in range(1,n+1):
        R=np.random.uniform(0,1,1)   #复合抽样法进行随机数的生成判断
        if R<=0.3:
            Y=np.random.uniform(0.5,0.8,1)
        else:
            U=np.random.uniform(0,1,1)
            a=125/7
            b=-190/7
            c=-0.8*0.8*a-b*0.8-U
            Y=(-b+np.sqrt(b**2-4*a*c))/(2*a)   #采用逆变换抽样法
        η.append(f(Y)/g(Y))
    re.append(np.mean(η))
print(f"重抽样法的估计值{np.mean(re)*2},方差{np.var(re)*4}")  #注意不能直接乘re,re为列表


######平均值估计法
re=[]
for i in range(1,m+1):
    U=np.random.uniform(0,1,n)
    re.append(np.mean(f(U)))
print(f"平均值估计法估计值{np.mean(re)},方差{np.var(re)}")

??§3.2.4 结果分析

??<-重要抽样法? ? ? ? ? ? ?平均值估计法 ->? ?

由上得到,重要抽样法要更为精确

§4.文章中的其他代码

§3.1图画

import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(0,1,1000)
y=np.exp(x)
plt.plot(x,y,color='blue')
plt.xlim([0,1])
plt.ylim([0,np.e])
z=(1+x)*(2/3)
plt.plot(x,z,color='red')
plt.show()

?§1图像

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=["SimHei"]
n=50
value=[]

n=20
x=np.random.uniform(low=0,high=2,size=10)
x=np.append(x,np.random.uniform(low=2,high=3,size=40))
y=x**5

plt.scatter(x,y,s=10,color='green')
for i in range(0,len(x)):
    plt.plot([x[i],x[i]],[x[i]**5,0],lw=1,color='green')
plt.plot(np.linspace(0,3,1000),np.linspace(0,3,1000)**5)
plt.axvline(x=2.0,color="red")
plt.xlim(0,3)
plt.ylim(0,3**5)
plt.text(0.8,200,"对于左侧区间使用少量样本(10)\n粗略估计")
plt.text(1,125,"A1")
plt.text(2.5,125,"A2")
plt.text(2,200,"对于右侧区间使用大量样本(40)\n精确估计")
plt.show()

??§3.1错误示范图像

f_1=function(x){
    return=x^-0.5*(1-x)^-0.5/pi
}
g_1=function(x){
    return=((x-0.5)^6+0.005)/0.007232143  #归一化的结果,使得g_1为密度函数
}


x=seq(from=0,to=1,by=0.01)
plot(x,f_1(x),type='l',xlim=c(0,1),ylim=c(0,4),col="blue")
lines(x,g_1(x),type="l",col="red")
legend("top",legend=c("f(x)","g(x)"),col=c("blue","red"),lty=1)

?§3.1.4结果分析

#########重要抽样法
set.seed(1)
m=10  #比较次数
n=1000
for (j in 1:m){
    re=NULL
g=function(x){
    return=2/3*(1+x)
}
f=function(x){
    return=exp(x)
}

U=runif(n)
Y=(3*U+1)^0.5-1
re[1]=mean(f(Y)/g(Y))

########平均值估计#####

U=runif(n)
re[2]=mean(f(U))
cat("第",j,"次实验","重要抽样法误差",abs(re[1]-1.71828),"平均值估计法误差",abs(re[2]-1.71828),"\n")
}

文章来源:https://blog.csdn.net/iotream/article/details/135317505
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！