（七）杂波中的IMM+JPDA+UKF滤波算法

目录

前言

一、基础知识

（一）IMM原理

（二）JPDA原理

（三）UKF原理

（四）算法流程图

二、仿真验证

（一）模型构建

（二）仿真结果

总结

参考文献

---

前言

????????本文介绍了一种杂波中的交互多模型（IMM）+联合概率数据互联（JPDA）+无迹卡尔曼滤波（UKF）算法。本文首先介绍了IMM算法和联合概率数据互联算法的基本原理，之后给出了两种算法的联合算法的流程图。本文注重于思路的讲解，关于算法的细节以及概念推导可以在提供的文献中查看。之后，根据算法的思想进行了对应仿真。仿真结果表明，所提算法能有效地对杂波中的目标进行追踪，验证了所提算法的有效性。

---

一、基础知识

（一）IMM原理

当目标运动状态发生改变时，一种模型已经不能准确描述目标的运动状态。因此需要建立模型集，通过估计目标与模型之间的相似程度来决定用哪种模型对目标运动状态进行描述。之前的博客中讲解了CV（匀速）、CA（匀加速）、CT（匀速转弯）模型的具体构建过程，可以从以下链接中获取。

? ? ? ? ? ? ? ? ? ? ? ? ? ? ?交互式多模型（IMM）中二维平面CV/CA/CT模型构建https://blog.csdn.net/h320130/article/details/135141783????????

????????模型集构建之后，需要通过计算各个模型之间的模型概率来合成目标的运动，具体过程如下图所示。具体的推导过程可以参考文献 [1]。

????????文章对应代码如下（部分）：

 for j = 1:n_target
            %输入交互
            c_j{j} = pij'*u_IMM{j}(:,i-1); %预测概率（归一化常数）
            u1 = pij(:,1).*u_IMM{j}(:,i-1)/c_j{j}(1);
            u2 = pij(:,2).*u_IMM{j}(:,i-1)/c_j{j}(2);
            u3 = pij(:,3).*u_IMM{j}(:,i-1)/c_j{j}(3);
            %模型混合状态计算
            X1 = X_CV{j}(:,i-1)*u1(1) + X_CA{j}(:,i-1)*u1(2) + X_CT{j}(:,i-1)*u1(3);
            X2 = X_CV{j}(:,i-1)*u2(1) + X_CA{j}(:,i-1)*u2(2) + X_CT{j}(:,i-1)*u2(3);
            X3 = X_CV{j}(:,i-1)*u3(1) + X_CA{j}(:,i-1)*u3(2) + X_CT{j}(:,i-1)*u3(3);
            %计算各模型初始状态协方差矩阵
            P1 = (P_CV{j,i-1}+(X_CV{j}(:,i-1)-X1)*(X_CV{j}(:,i-1)-X1)')*u1(1)+...%计算各模型初始状态协方差矩阵
                (P_CA{j,i-1}+(X_CA{j}(:,i-1)-X1)*(X_CA{j}(:,i-1)-X1)')*u1(2)+...
                (P_CT{j,i-1}+(X_CT{j}(:,i-1)-X1)*(X_CT{j}(:,i-1)-X1)')*u1(3);
            P2 = (P_CV{j,i-1}+(X_CV{j}(:,i-1)-X2)*(X_CV{j}(:,i-1)-X2)')*u2(1)+...%计算各模型初始状态协方差矩阵
                (P_CA{j,i-1}+(X_CA{j}(:,i-1)-X2)*(X_CA{j}(:,i-1)-X2)')*u2(2)+...
                (P_CT{j,i-1}+(X_CT{j}(:,i-1)-X2)*(X_CT{j}(:,i-1)-X2)')*u2(3);
            P3 = (P_CV{j,i-1}+(X_CV{j}(:,i-1)-X3)*(X_CV{j}(:,i-1)-X3)')*u3(1)+...%计算各模型初始状态协方差矩阵
                (P_CA{j,i-1}+(X_CA{j}(:,i-1)-X3)*(X_CA{j}(:,i-1)-X3)')*u3(2)+...
                (P_CT{j,i-1}+(X_CT{j}(:,i-1)-X3)*(X_CT{j}(:,i-1)-X3)')*u3(3);
        end

（二）JPDA原理

????????联合概率数据互联（JPDA）算法是进行杂波条件下多目标数据互联的有效算法。与单目标条件下应用的概率数据互联（PDA）算法相似，JPDA 也是通过波门内的所有量测计算一个加权新息用于航迹更新。算法的核心在于，当有量测进入不同目标跟踪波门的重合区域时，此时要综合考虑量测来自不同目标之间的概率。在计算互联概率的时候，要考虑不同目标对于量测的竞争，对应的权值需要减小，以体现其他目标的竞争。具体可以分为以下几步，对应部分的代码分别为：

????????1.确认矩阵计算

for i = 1:n_ev%全部是按照从上往下，按照列的顺序进行的，第一个目标第一种模型的
    Z_mid_pre = zeros(nz,n_target) ;
    X_mid_pre = zeros(nx,n_target) ;
    S_mid_pre = cell(1,n_target);
    S_mid_pre(:) = {zeros(nx,nx)};
    for j = 1 : n_target
        %构造单个的观测矩阵
        X_mid_pre(:,j) = X_mix_pre{j}(:,c(i,j));
        P_mid_pre = P_mix_pre{c(i,j),j};
        [Z_mid_pre(:,j),S_mid_pre{j},~] = UT(X_mid_pre(:,j),P_mid_pre,R{j},nx,nz);
    end
    

????????2.互联矩阵计算

[n1,n2] = size(Q2);
x1 = sum(Q2,2);
n_total = 1;
for i = 1:n1
    n_total = n_total * x1(i);
end
index = index_pro(x1');
c_lib = cell(1,n1);
for i = 1:n1
    c_lib{i} =cell(1,x1(i));
end

????????3.互联概率计算

    %计算总的关联概率
    U=zeros(m1+1,n_target);
    for i1=1:n_target
        for j=1:m1
            for k=1:num
                U(j,i1)=U(j,i1)+Pr(k)*A_matrix(j,i1+1,k);
            end
        end
    end
    U(m1+1,:)=1-sum(U(1:m1,1:n_target)); %无量测与目标T互联的关联概率存入U（m1+1,:),规一化
    U_index{i} = U;

（三）UKF原理

????????无迹卡尔曼滤波（UKF）算法的核心就是利用无迹变换（UT）处理均值和协方差。 无迹变换（UT）是指在估计点附近进行确定性采样，用这些采样点的高斯密度近似状态的概率密度函数。实现方法：在原状态分布中按照一定规则选取一些采样点，使这些采样点的均值和协方差等于原始状态的均值和协方差；将这些点带入非线性函数汇总，得到相应的非线性函数值点集，通过这些点集求取变换后的均值和协方差，这样得到的非线性变换的均值和协方差最少有二阶精度。对于高斯分布来说，可以达到三阶精度，其采样点的选择是基于先验均值和先验协方差矩阵的平方根的相关列实现的。对应详细的过程可以在以下链接中查看。

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?多传感器无迹卡尔曼滤波（UKF）跟踪正弦波https://blog.csdn.net/h320130/article/details/134918089

对应代码（部分）为：

function [X_output,P_output,E,P_zz] = UKF(X,P,Z,F,Q,R)
%无迹卡尔曼滤波

%%
%参数设定
L = 6; %状态维数
alpha = 1;
kalpha = 0;
belta = 2;
ramda = 3-L;
%%
%计算权值
for j = 1:2*L+1
    Wm(j) = 1/(2*(L+ramda));
    Wc(j) = 1/(2*(L+ramda));
end
Wm(1) = ramda/(L+ramda);
Wc(1) = ramda/(L+ramda)+1-alpha^2+belta;

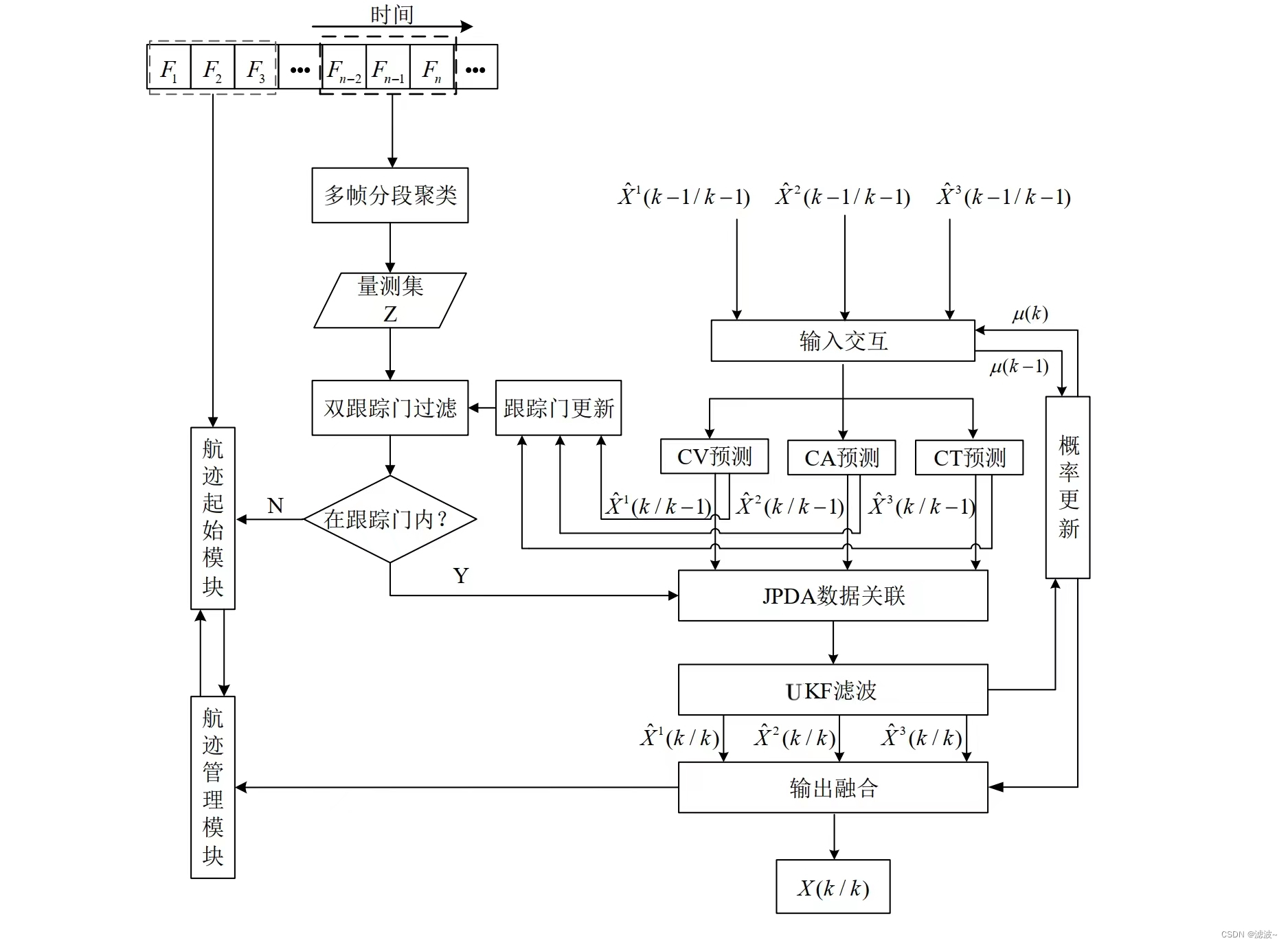
（四）算法流程图

? ? ? ? 对应仿真过程的流程图如下，具体过程复现可以参考文献 [2] 中的内容，里面有详细步骤。

?

二、仿真验证

（一）模型构建

????????假设有三个目标，分别以不同的初速度在不同的阶段采用不同的模型进行运动。设定如下：

%目标运动参数定义,运动轨迹和量测轨迹产生
time_index = cell(2,n_target);%每个元组里面包含两个信息，即一个包含起始终止时刻，类别和加速度；一个是初始状态信息
time_index{1,1} = 
   [1 30 1 0 0
    31 60 3 4*2*pi/360 0
    61 90 2 -6 -2]; %第一列和第二列表示开始和结束时刻；第三列表示模型的类别；如果为1模型，第四列和第五列为空，表示x和y的加速度
time_index{2,1} = [-400,40,0,200,35,0]';%表示第一个目标的初始状态信息

time_index{1,2} = 
   [1 30 1 0 0
    31 60 3 1*2*pi/360 0
    61 90 2 10 -3];  %第一列和第二列表示开始和结束时刻；第三列表示模型的类别；如果为1模型，第四列和第五列为空，表示x和y的加速度
time_index{2,2} = [-10,-40,0,320,25,0 ]';%表示第二个目标的初始状态信息

time_index{1,3} = 
   [1 40 1 0 0
    41 80 2 5 -6
    81 90 3 5*2*pi/360 0];  %第一列和第二列表示开始和结束时刻；第三列表示模型的类别；如果为1模型，第四列和第五列为空，表示x和y的加速度
time_index{2,3} = [500,-50,0,-120,25,0 ]';%表示第二个目标的初始状态信息

????????部分参数设定如下：

%参数设定部分
T = 1;%采样时间S
n_target = 3 ; %目标数量
n_end = 90; %结束时刻
nf = [0.01, 0.01, 0.01]; %CV,CA,CT模型的过程噪声
nx = 6; %状态向量维数
nz = 2; %量测向量维数
nt = 3; %模型集的模型数量
clutter_density = 0.00001; %杂波密度

（二）仿真结果

????????按照上述设置参数进行仿真后得到杂波中的点迹图和各个目标的概率模型图如下：

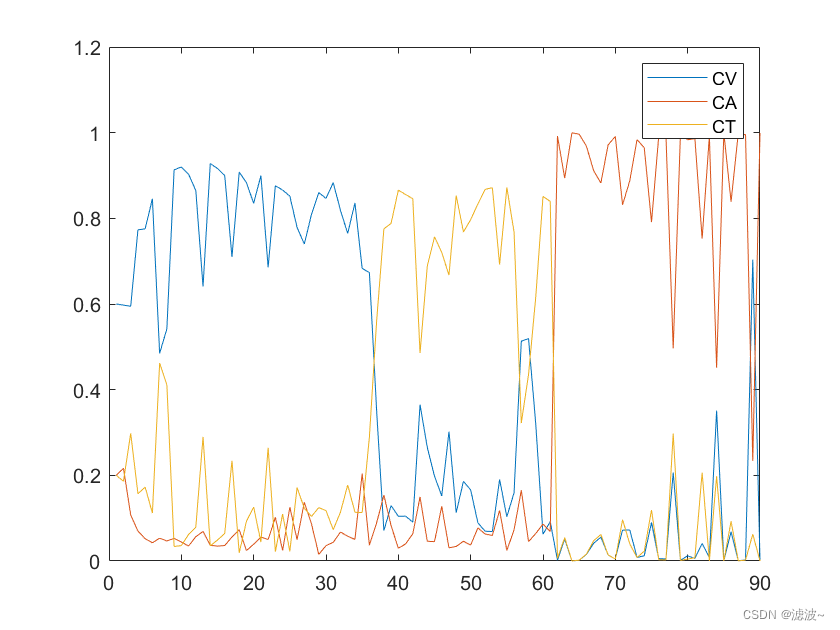
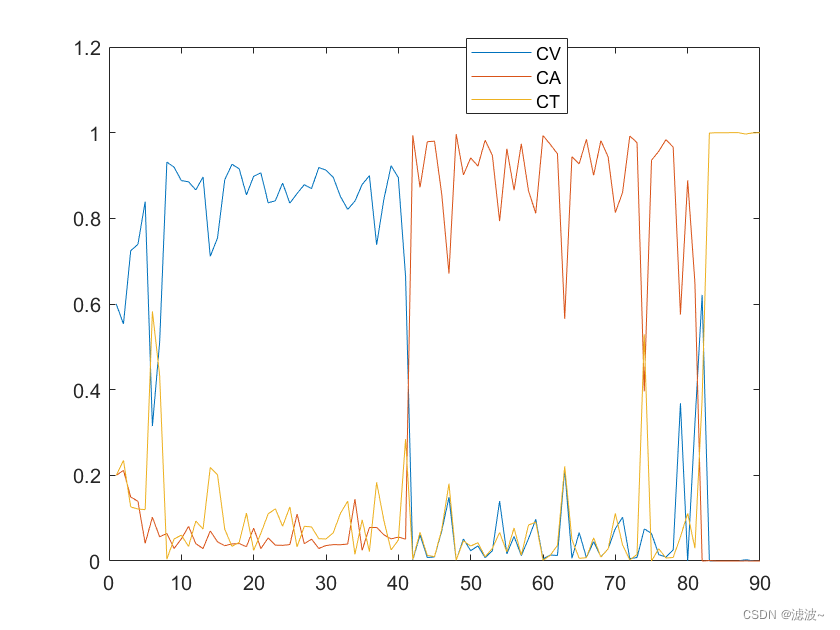
????????以上仿真结果表明，所提算法能有效识别目标的运动模型种类，并将杂波中的量测信息与各个目标相关联，证明了所提算法的有效性。

---

总结

? ? ? ? 本文提出了一种杂波中的IMM+JPDA+UKF算法，可以有效识别各个目标的运动模型，从而实现杂波中多目标的有效跟踪。下一步将继续添加航迹管理部分，将航迹起始和航迹终结算法加入到算法中，进而实现更加真实的仿真模拟。

参考文献

[1] William J Farrell. Interacting multiple model filter for tactical ballistic missile tracking. IEEE Transactions on Aerospace and Electronic Systems, 44(2):418–426, 2008.

[2] 胡小龙. 跟踪多机动目标的多模型滤波算法研究[D].哈尔滨工程大学, 2021.