机器学习理论U1 概念介绍和入门
文章目录
一、概念
机器学习的基本思想是让计算机通过从大量数据中学习模式、规律和趋势,并使用这些学习到的知识来做出预测、分类或决策。它依赖于统计学、概率论和优化理论等数学方法,通过构建和训练模型来实现任务的自动化。
二、相关邻域
模式识别,数据挖掘,计算机视觉,自然语言处理。
三、分类
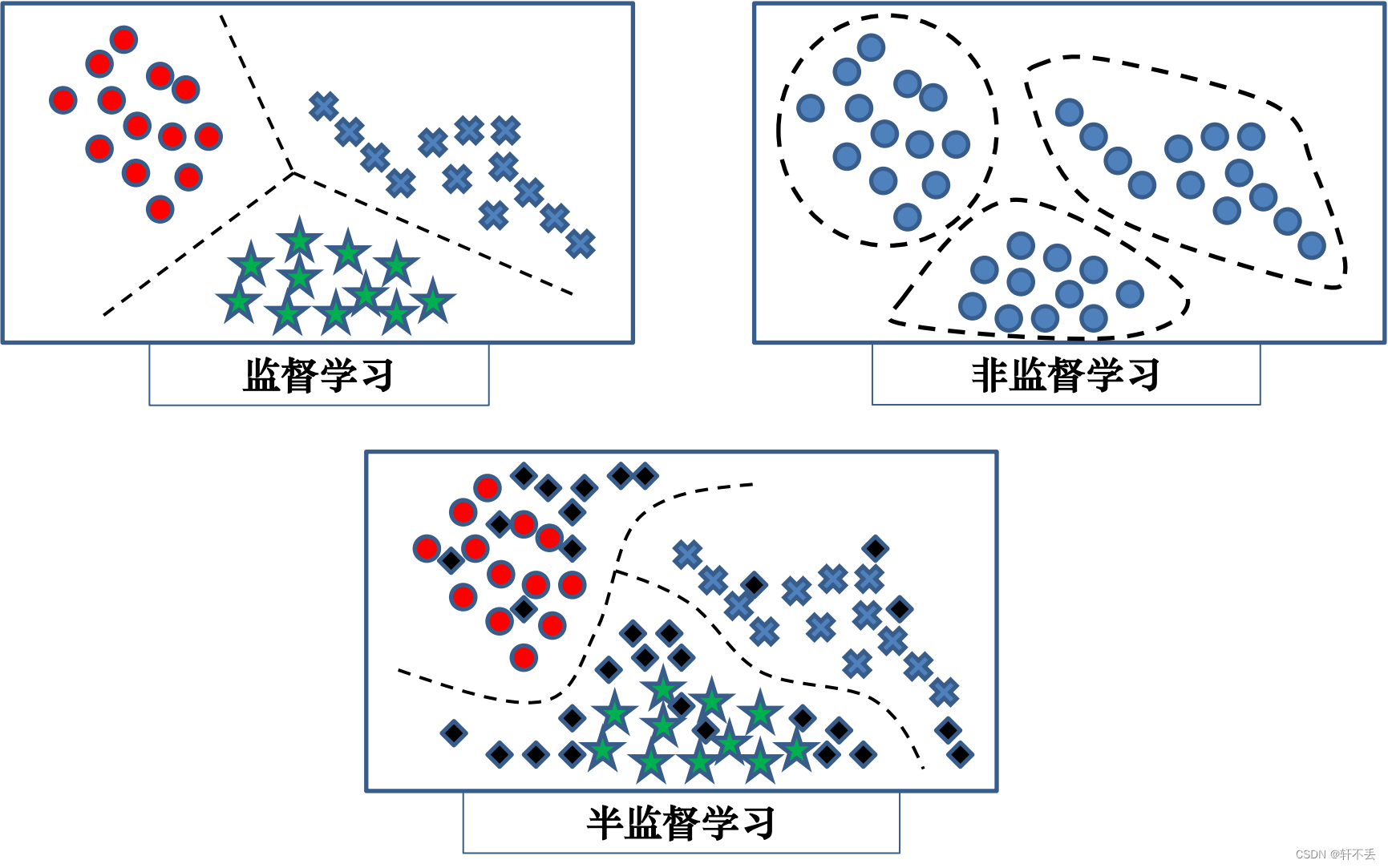
1、主要研究问题
分类 聚类 回归 降维
四、模型评估和选择
1、模型性能
同一问题,多种算法/模型。分类问题:贝叶斯决策、决策树、SVM…
同一算法/模型,不同参数配置
2、误差
误差(error):算法/模型的实际预测输出与样本的真实输出之间的差异
训练误差/经验误差(training/empirical error):学习器在训练集上的误差。
泛化误差(generalization error):学习器在新样本上的误差
最终的目标是泛化误差。但模型的搭建只能得出训练误差,因此要进行转换
3、模型评估选择的步骤
- 对数据集进行划分,分为训练集和测试集两部分
- 在训练集上训练得到模型
- 对模型在测试集上面的泛化性能进行度量
- 基于测试集上的泛化性能,依据假设检验来推广到全部数据集上面的泛化性能
五、数据集的划分
1、划分方式
1)方式一
目标:将数据集D划分为训练集S和测试集T两部分,在训练集上训练模型,然后在测试集上评估其性能。
原则:测试集应尽量与训练集互斥;即测试样本尽量不在训练集中出现,未在训练过程中使用。
2)方式二
将数据集D划分为训练集S、验证集V和测试集T三部分,在训练集上训练模型,在验证集上调整模型超参数,并对模型的能力(是否过拟合)进行初步评估和选择,在验证集上然后在测试集上评估其性能。
原则:测试集、验证集应尽量与训练集互斥;即验证样本、测试样本尽量不在训练集中出现,未在训练过程中使用。
2、划分方法
保持/留出法(hold-out) :给定数据随机地划分到两个独立的集合:训练集和测试集。通常,2/3的数据分配到训练集,其余1/3分配到测试集。使用训练集导出模型,用测试集来估计泛化误差。
随机子抽样(random sub-sampling):保持方法的一种变形;随机地选择训练集和测试集,将保持方法重复k次,总准确率估计取每次迭代准确率的平均值。
k折交叉验证(k-fold cross-validation):初始数据数据被划分成 k 个大小相似、互不相交的子集/”折”。训练和测试 k 次;在第 i 次迭代,第 i 折用作测试集,其余的子集都用于训练学习,取 k 次测试结果的均值。
与保持法和随机子抽样法不同,这里每个样本用于训练的次数相同,并且用于检验一次。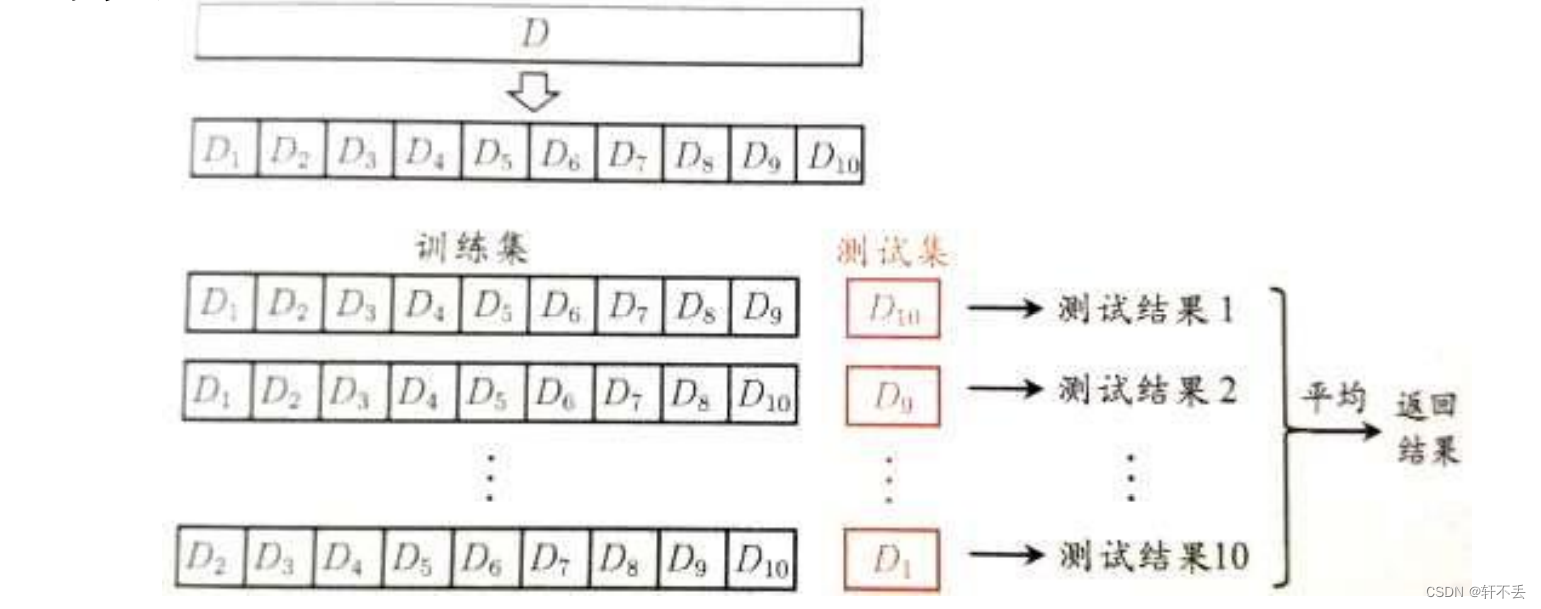
自助法(bootstrapping):从初始样本
D
D
D中有放回均匀抽样;即每当选中一个样本,它等可能地被再次选中并再次添加到训练集中;采样
∣
D
∣
|D|
∣D∣次后,即可获取大小为
∣
D
∣
|D|
∣D∣的训练样本集;没有进入训练集的数据样本形成测试集。
优势:可产生多个不同训练样本集;对于小数据集,自助法效果胜过K折交叉验证;能从初始数据集中产生多个不同的训练集,这对集成学习等方法有很大的好处。
缺点:改变了数据集分布,会引入估计偏差。
六、性能度量
1、回归任务
均方误差(Mean Squared Error): E ( f ; D ) = 1 n ∑ i = 1 n ( f ( x i ) ? y i ) 2 E(f;D) = \frac{1}{n} \sum_{i=1}^n (f(x_i)-y_i)^2 E(f;D)=n1?∑i=1n?(f(xi?)?yi?)2
更一般情况:对于数据分布
D
D
D 和概率密度函数
p
(
?
)
p(·)
p(?),均方误差可描述为:
E
(
f
;
D
)
=
∫
x
?
D
(
f
(
x
i
)
?
y
i
)
2
p
(
X
)
d
x
E(f;D) = \int_{x-D}(f(x_i)-y_i)^2 p(X)dx
E(f;D)=∫x?D?(f(xi?)?yi?)2p(X)dx
f
f
f:训练的学习器
D
D
D:初始样本集,
D
=
D =
D={
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
…
,
(
x
n
,
y
n
)
(x_1, y_1), (x_2, y_2),…,(x_n, y_n)
(x1?,y1?),(x2?,y2?),…,(xn?,yn?)}
y
i
y_i
yi? :样本输入
x
i
x_i
xi?的真实标记
2、分类任务
错误率:
E
(
f
;
D
)
=
1
n
∑
i
=
1
n
Π
(
f
(
x
i
)
≠
y
i
)
E(f;D) = \frac{1}{n} \sum_{i=1}^n Π(f(x_i)\neq y_i)
E(f;D)=n1?∑i=1n?Π(f(xi?)=yi?)
精度:
a
c
c
(
f
;
D
)
=
1
n
∑
i
=
1
n
Π
(
f
(
x
i
)
=
y
i
)
=
1
?
E
(
f
;
D
)
acc(f;D) = \frac{1}{n} \sum_{i=1}^n Π(f(x_i) = y_i) = 1-E(f;D)
acc(f;D)=n1?∑i=1n?Π(f(xi?)=yi?)=1?E(f;D)
3、混淆矩阵
用来作为分类规则特征的表示,它包括了每一类的样本个数,包括正确的和错误的分类

?
T
P
TP
TP :被分类器正确分类的正元组;期望为
P
P
P,分类为
P
P
P:称为真正
?
T
N
TN
TN:被分类器正确分类的负元组; 期望为
N
N
N,分类为
N
N
N:称为真负
?
F
P
FP
FP:被错误标记为正元组的负元组; 期望为
N
N
N,分类为
P
P
P:称为假正
?
F
N
FN
FN:被错误标记为负元组的正元组。期望为
P
P
P,分类为
N
N
N:称为假负
? 准确率(识别率):评估分类器正确识别正、负样本的能力
a
c
c
u
r
a
c
y
=
T
P
+
T
N
P
+
N
accuracy = \frac{TP+TN}{P+N}
accuracy=P+NTP+TN?
? 错误率:评估分类器错误识别正、负样本的能力
E
r
r
o
r
R
a
t
e
=
F
P
+
F
N
P
+
N
ErrorRate = \frac{FP+FN}{P+N}
ErrorRate=P+NFP+FN?
? 真阳性率(
T
P
R
TPR
TPR):评估分类器正确识别正样本的能力
S
N
=
T
P
P
=
T
P
T
P
+
F
N
SN = \frac{TP}{P} = \frac{TP}{TP+FN}
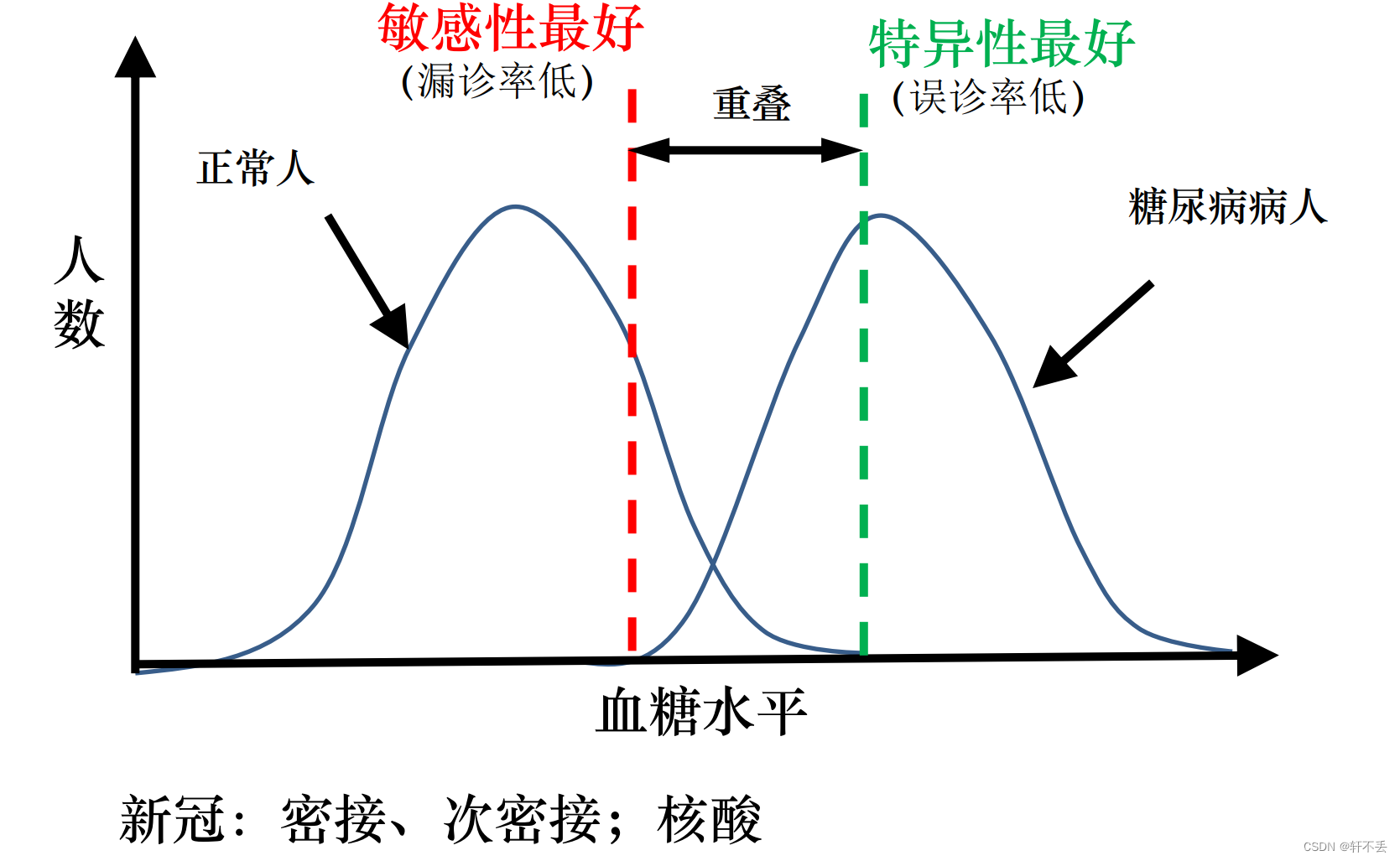
SN=PTP?=TP+FNTP? 敏感性(sensitivity)
? 真阴性率(
T
N
R
TNR
TNR):评估分类器正确识别负样本的能力
S
P
=
T
N
N
=
T
N
T
N
+
F
P
SP = \frac{TN}{N} = \frac{TN}{TN+FP}
SP=NTN?=TN+FPTN? 特异性(specificity)
? 精度/查准率(precision):评估预测正样本中的真正样本
p
e
r
c
i
s
i
o
n
=
T
P
T
P
+
F
P
percision = \frac{TP}{TP+FP}
percision=TP+FPTP?
? 召回率/查全率(Recall):评估分类器正确识别正样本的能力,等价于敏感性
r
e
c
a
l
l
=
T
P
T
P
+
F
N
recall = \frac{TP}{TP+FN}
recall=TP+FNTP?
查准率和查全率互相矛盾。查准率高,则查全率低;反之亦然
P
?
R
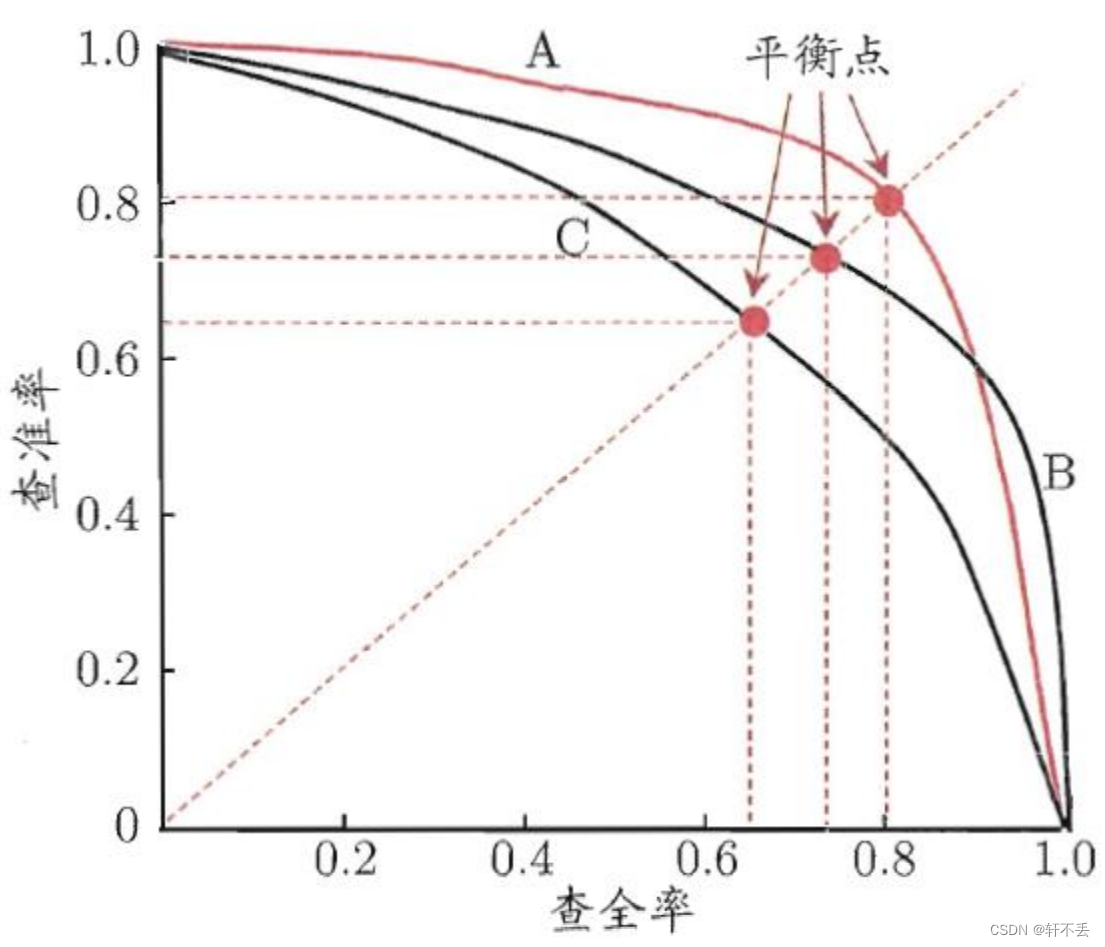
曲线
P-R曲线
P?R曲线
以查全率R为横轴,查准率P为纵轴,根据模型预测结果对样本进行排序,把最可能是正样本个体排在前面,而后面的则是模型认为最不可能为正例的样本,再按此顺序逐个把样本作为正例进行预测并计算出当前的查准率和查全率得到的曲线。
F
1
度量
F1度量
F1度量:查准率和查全率的调和平均,推荐系统常用
1
F
1
=
1
2
(
1
p
r
e
c
i
s
i
o
n
+
1
r
e
c
a
l
l
)
\frac{1}{F_1} = \frac{1}{2}(\frac{1}{precision}+\frac{1}{recall})
F1?1?=21?(precision1?+recall1?)
F 1 = 2 ? p r e c i s i o n ? r e c a l l p r e c i s i o n + r e c a l l F_1 = \frac{2*precision*recall}{precision+recall} F1?=precision+recall2?precision?recall?
F β F_β Fβ?度量: F 1 F_1 F1?度量的一般形式,利用参数 β β β控制查全率对查准率的相对重要性; β = 1 β=1 β=1时,退化为 F 1 F_1 F1?; β > 1 β>1 β>1时,查全率有更高大影响; β < 1 β<1 β<1时,查准率有更高大影响
F β = ( 1 + β 2 ) ? p r e c i s i o n ? r e c a l l β 2 ? p r e c i s i o n + r e c a l l F_β = \frac{(1+β^2)*precision*recall}{β^2*precision+recall} Fβ?=β2?precision+recall(1+β2)?precision?recall?
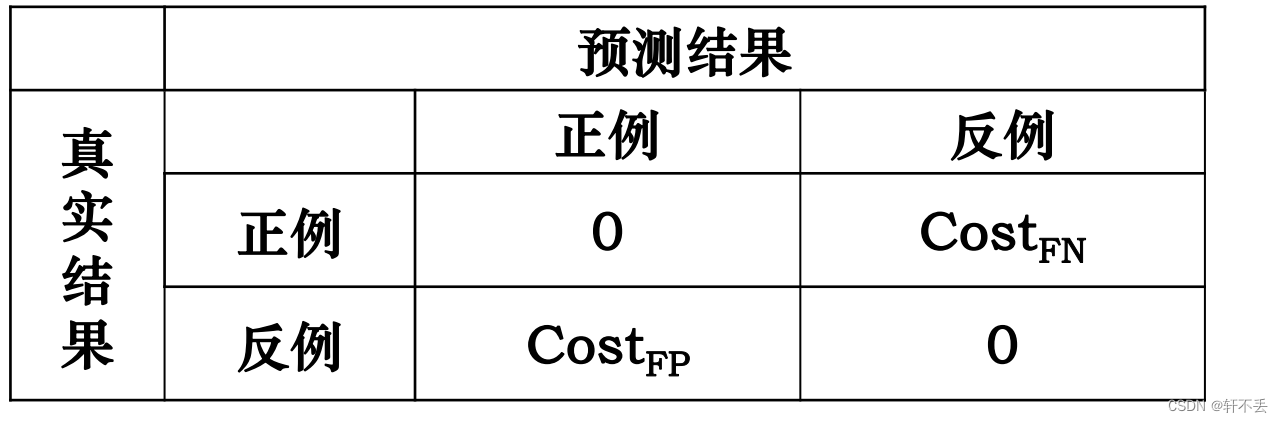
4、代价矩阵
描述不同错误的不同代价/风险
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Java IO 基础知识总结
- 超低温冰箱这个技术,简单又直观!
- [PyWinAuto]模拟键鼠输入
- 2.3_2 进程互斥的软件实现方法
- 百度搜索品牌形象优化怎么做?
- 大创项目推荐 深度学习人体跌倒检测 -yolo 机器视觉 opencv python
- H5向微信小程序发送信息(小程序web-view打开H5)
- Spring Boot中关闭Job任务
- Python数据分析:活用Pandas库
- ES6之Promise的链式调用