语法树的画法(根据文法求字符串)
目录
1.语法树的画法
文法G[E]:E->E+E | E*E | (E) | i ,字符串 i+i*i
推导方式有两种最左推导和最右推导(推导的技巧就是逐步靠近字符串的形式)
最左推导(从左往右替换):
E->E+E->i+E->i+E*E->i+i*E->i+i*i
最左推导得到的语法树如下: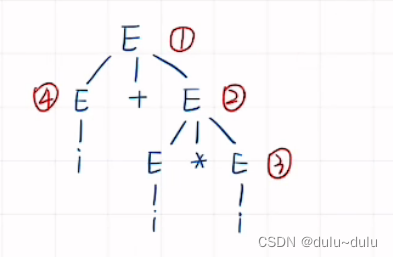
最右推导(从右往左替换):
E->E+E->E+E*E->E+E*i->E+i*i->i+i*i
最右推导得出的语法树:

如果两种推导画出来的树相同,则说明他们有无二义性,如果树不同就是有二义性
2.语法树的短语
一个节点的最根部就是这个节点的短语,那么短语有几个呢,就看语法树中有分支的字符有几个,就有几个短语

由上图分析,第一个节点(①)的短语是i+i*i? ? ? ? 第二个节点的短语i*i? ? ? ? ? ? ③④⑤的短语为i
3.直接短语(直接到根部)
所以上面这棵语法树的直接短语就是i,例如这里的直接短语就是 S,a(注意"("")"不是直接短语)
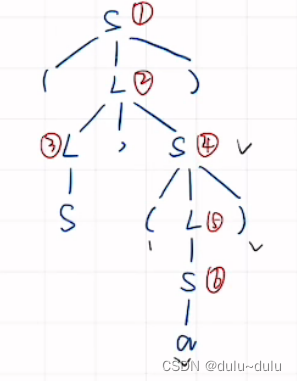
4.素短语
寻找素短语的前提是在短语中找,这些短语要满足以下条件
(1)至少包含一个终结符
(2)该短语不再包含满足第一个条件的更小的短语
由上面的语法树可以得到的语法为①i+i*i? ? ? ? ②i*i? ? ? ? ③i
①i+i*i,其中包含了满足第一个条件的②
②i*i,包含了满足第一个条件的③
所以素短语只有③
注:有些地方会提到最左素短语,最左素短语就是素短语中位于语法树最左的字符
5.句柄
最左最小的树对应的符号串,或者是直接短语中最左的符号串,在上面的语法树中,句柄就是i
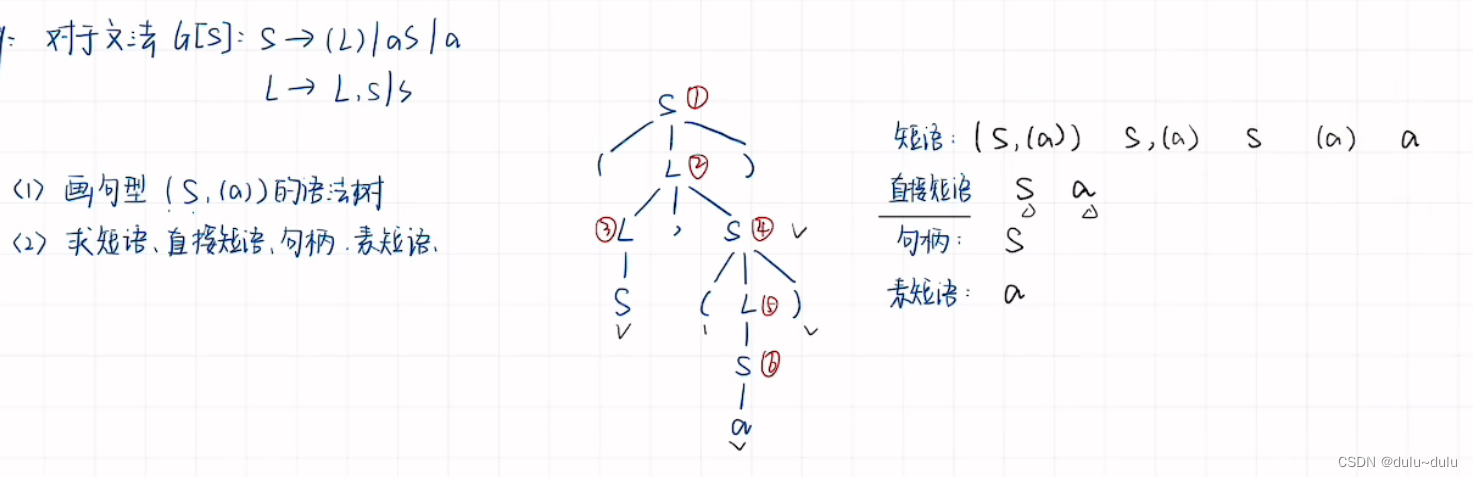
例题1:
这里注意T+T也是素短语,因为他不包含满足第一个条件的短语

例题2:
消除左递归和消除回溯(这一部分比较难,还是要多做题感受下)
消除左递归:
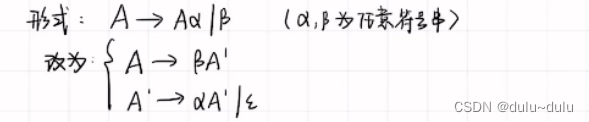
例题1:
E-->E+T|T:
① 将T提前,其他改写为文法E':E->TE'
②剩下的写下来,"|"右边的T由于已经被提出来所以变为(空串):E'--->+TE'|
T-->T*F|F:
①T--->FT'
②*FT'|
F-->(E)|i:不符合左递归的形式,所以照搬即可
例题2:

消除回溯:

例题1:G[A] = A->aAB|a|b
①:将公共左因子"a"提走,另一部分改写为A',没有公共左因子的照抄:A-->aA'|b
②:将改造后的文法A'补齐:A'-->AB|
例题2:
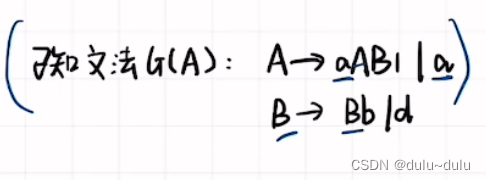

6.算符优先分析句型
若有句型......
....,当
属于句柄时,则
?和
也在句柄中,这是由于算符文法的任何句型中均无两个相邻的非终结符,且终结符和非终结符相邻时,含终结符的句柄必含相邻的非终结符,句柄终结符之间的关系如下:
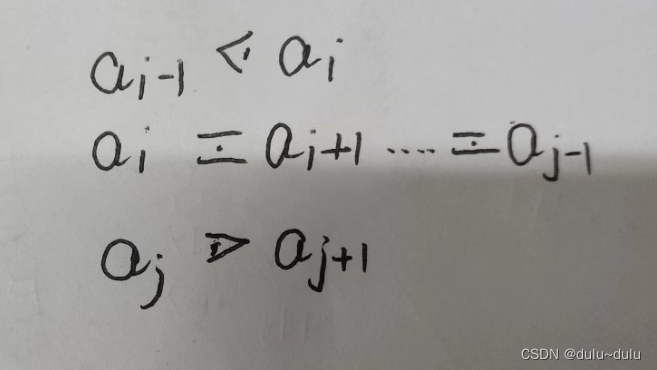
例题:
?
第一步:需要将算符优先分析表得出来
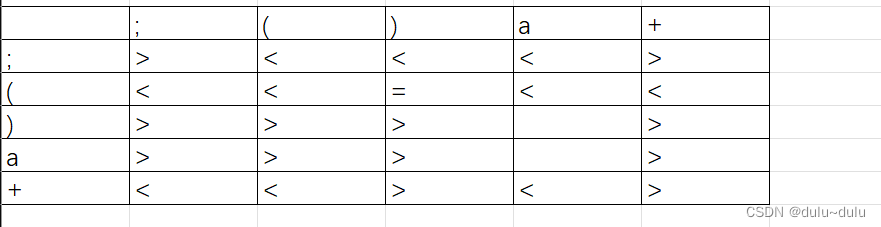
这可以看:算符优先分析的方法
第二步:进行算符优先分析
①默认的#是小于当前输入符号(a)的,所以动作为移入
②接下来继续看栈顶的终结符(a),#<a且a>;所以a就形成了句柄
③对句柄进行归约

由式子可以看到:H->a|(S),可以看到句柄a可以归约为H,但是由于这里是算符优先级分析,?只考虑终结符,所以写任何非终结符是没有关系的,所以这里也可以写T
由于栈中最顶层的终结符为#,又因为#<;所以继续移进

接下来继续下一步的操作:
这里最顶层的终结符a满足,a>+,且"("< "a",所以a是这个整个语句的句柄,继续归约为T
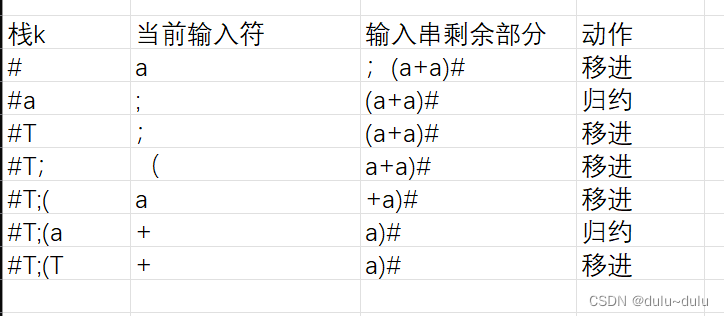
继续下一步操作:
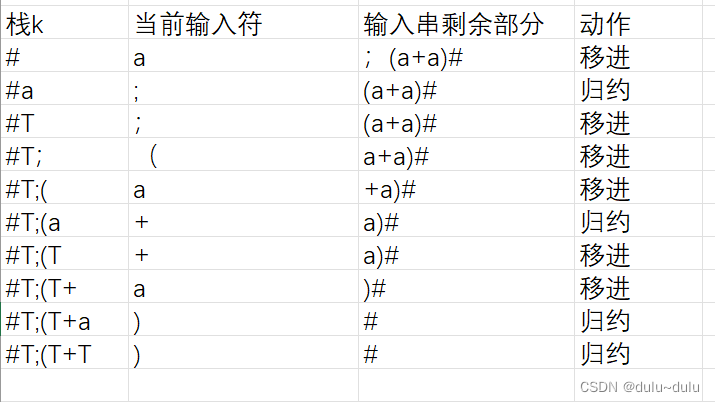
此时最顶层的终结符为+,因为“(”<"+",且“+” > ")",所以+为句柄,又因为,两端有两个非终结符,也在句柄中,所以由T-->T+S|S ,形似T+S,将“T+T”归约为T
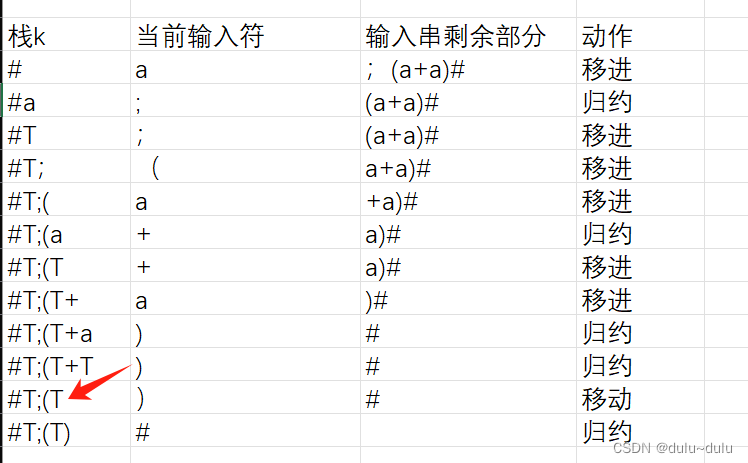
由于“(“=”)“,且";"?< "(" ,所以这里的"("是句柄,由于公式中含有H->G|(S),所以我们可以将其归约为H,但是这里非终结符是什么没有关系,所以统一归结为T
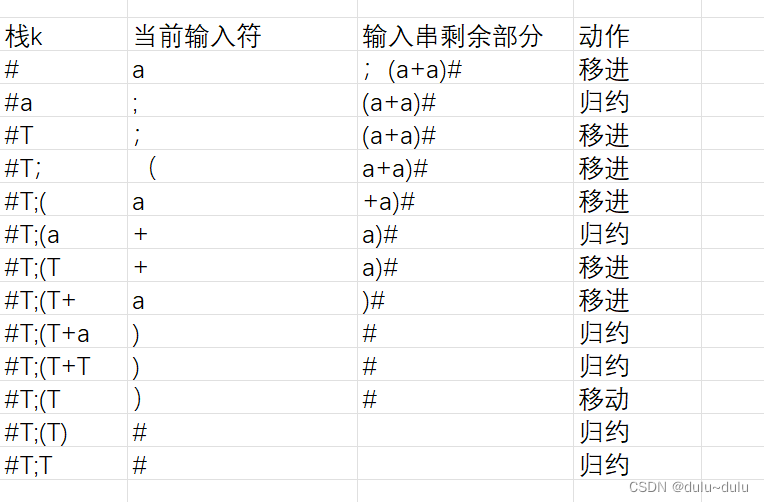
由于式子中包含S-->S;G|G,这里还是可以归约为S,但是同理我们归约为非终结符T也没有影响
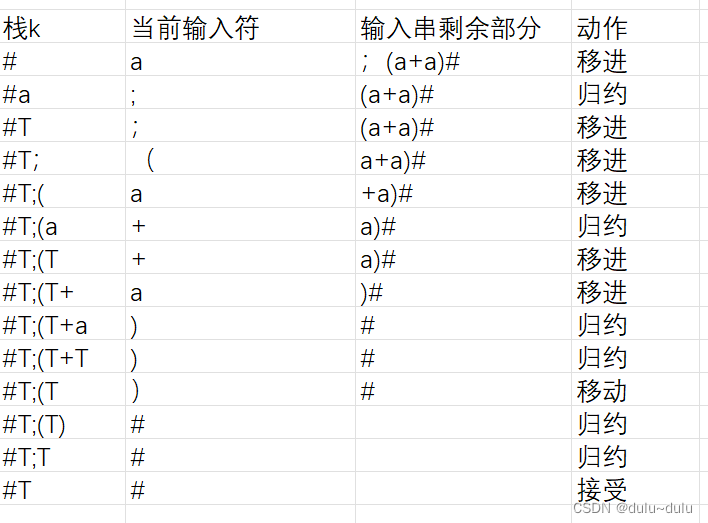
所以可得结论:a;(a+a)是G[S]文法中推出来的
但是这里我们注意:a;(a+a)的最右推导,无法推导出a;(a+a),所以a;(a+a)不是G[S]文法的句子

这与算符优先分析中的结论矛盾了,但是最右推导属于规范推导,正确答案是: (不是)
所以算符优先分析可能会错误地接受非法的句子,其推导的过程不规范。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- vue3中vite.config.js文件常用配置
- Python桌面开发技术 PyQt6教程专栏 一周快速上手,开发桌面应用
- 创建Servlet的三种方式
- 3ds Max渲染效果图噪点多,正确设置渲染参数很重要
- openGauss学习笔记-188 openGauss 数据库运维-常见故障定位案例-core问题定位
- 业绩与股价相背离,市值半年缩水800亿元,金山办公前途何方?
- 39、平均池化和全局平均池化
- python中的pprint
- MCU平台下确定栈空间大小的方法
- 编程式事务和声明式事务什么区别