力扣:51. N 皇后
发布时间:2023年12月25日
题目:
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n?皇后问题?研究的是如何将?n?个皇后放置在?n×n?的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数?n?,返回所有不同的?n?皇后问题?的解决方案。
每一种解法包含一个不同的?n 皇后问题?的棋子放置方案,该方案中?'Q'?和?'.'?分别代表了皇后和空位。
示例 1:
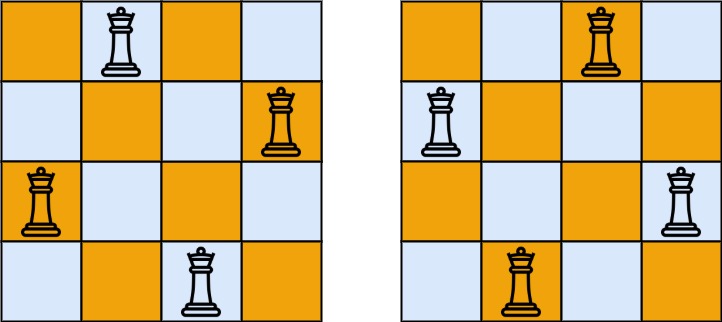
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:[["Q"]]
提示:
1 <= n <= 9
思路:
n皇后问题是回溯算法解决的经典问题,但该回溯是解决二维矩阵,跟之前题目还有所不同。
首先来看一下皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
def is_valid(self, n, row, col, chessboard):
for i in range(row): # 检查同一列是否有皇后
if chessboard[i][col] == 'Q':
return False
i, j = row - 1, col - 1
while i >= 0 and j >= 0: # 检查左对角线上是否有皇后
if chessboard[i][j] == 'Q':
return False
i -= 1
j -= 1
i, j = row - 1, col + 1
while i >= 0 and j < n: # 检查右对角线上是否有皇后
if chessboard[i][j] == 'Q':
return False
i -= 1
j += 1
return True?之后就是回溯的模板了
def backtracking(self, 参数):
if (终止条件):
存放结果
return
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)
处理节点
self.backtracking(路径,选择列表) # 递归
回溯,撤销处理结果?找到的所有结果都是要先判断皇后位置是否合规,最后集合里都是合规的解
def backtracking(self, n, chessboard, row, result):
if row == n:
result.append(chessboard[:])
return
for col in range(n):
if self.is_valid(n, row, col, chessboard):
chessboard[row] = chessboard[row][:col] + 'Q' + chessboard[row][col + 1:]
self.backtracking(n, chessboard, row + 1, result)
chessboard[row] = chessboard[row][:col] + '.' + chessboard[row][col + 1:]?本题还有一个难点就是创建棋盘和将解决方案转换成所需格式
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
result = [] # 初始化一个空列表来存储解决方案
chessboard = ['.' * n for _ in range(n)] # 创建一个空的棋盘,使用'.'表示空白格子
self.backtracking(n, chessboard, 0, result) # 使用空棋盘和第一行开始回溯算法
return [[''.join(row) for row in solution] for solution in result] # 将解决方案转换为所需的格式chessboard = ['.' * n for _ in range(n)]?这行代码创建了一个名为"chessboard"的列表,其中包含n个字符串。每个字符串由n个'.'字符组成。在for循环中,下划线是一个占位符变量,它在循环中未被使用。这样就创建了一个具有n行和n列的国际象棋棋盘的二维表示,其中每个单元格由一个'.'字符表示。
return [[''.join(row) for row in solution] for solution in result]当我们使用
return [[''.join(row) for row in solution] for solution in result]这行代码时,它实际上是一个嵌套的列表推导式。
for solution in result:这部分遍历了result列表中的每一个解(solution)。[''.join(row) for row in solution]:这部分对于每个解(solution)都进行了处理。它使用了另一个列表推导式,遍历了solution中的每一行(row),并使用''.join(row)将每一行连接起来,形成一个完整的棋盘状态字符串。- 最终,外部的列表推导式
[... for solution in result]将每个处理后的解组成一个新的列表,这个列表包含了所有解的字符串表示形式。所以,整体来说,这行代码的作用是将result中的每个解转换为字符串列表的形式,并将这些字符串列表组成一个新的列表作为返回值。
代码:
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
result = [] # 初始化一个空列表来存储解决方案
chessboard = ['.' * n for _ in range(n)] # 创建一个空的棋盘,使用'.'表示空白格子
self.backtracking(n, chessboard, 0, result) # 使用空棋盘和第一行开始回溯算法
return [[''.join(row) for row in solution] for solution in result] # 将解决方案转换为所需的格式
def backtracking(self, n, chessboard, row, result):
if row == n: # 如果所有皇后都被放置(基本情况),将当前配置添加到结果中
result.append(chessboard[:])
return
for col in range(n): # 遍历当前行的每一列
if self.is_valid(n, row, col, chessboard): # 检查是否可以在当前位置放置皇后
chessboard[row] = chessboard[row][:col] + 'Q' + chessboard[row][col + 1:] # 放置皇后
self.backtracking(n, chessboard, row + 1, result) # 递归放置下一个皇后
chessboard[row] = chessboard[row][:col] + '.' + chessboard[row][col + 1:] # 回溯,移除皇后
def is_valid(self, n, row, col, chessboard):
for i in range(row): # 检查同一列是否有皇后
if chessboard[i][col] == 'Q':
return False
i, j = row - 1, col - 1
while i >= 0 and j >= 0: # 检查左对角线上是否有皇后
if chessboard[i][j] == 'Q':
return False
i -= 1
j -= 1
i, j = row - 1, col + 1
while i >= 0 and j < n: # 检查右对角线上是否有皇后
if chessboard[i][j] == 'Q':
return False
i -= 1
j += 1
return True
文章来源:https://blog.csdn.net/2301_77160836/article/details/135188924
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Backtrader 文档学习-Order Management and Execution
- 【23年新算法】分类预测 | Matlab实现SCSO-SVM基于沙猫群优化算法优化支持向量机的多变量分类预测
- YOLOv8_测试yolov8n.pt,yolov8m.pt训练的时间和效果、推理一张图片所需时间_解决训练时进程被终止killed
- 系统架构演变
- k8s的图形化工具rancher
- 录制完视频如何去除重复部分?
- MW Open - 高效率的API接口管理工具
- Python列表(List)、元组(Tuple)、字典(Dictionary)详解
- 基于GD32F103移植freemodbus从机库
- MySQL夯实之路-索引深入浅出