回溯法:N皇后问题

问题背景

八皇后问题是十九世纪著名的数学家高斯于1850年提出的。

? 问题是：在8×8的棋盘上摆放八个皇后， 使其不能互相攻击， 即任意两个皇后都不能处于同一行、 同一列或同一斜线上。

? n皇后问题：即在n× n的棋盘上摆放n个皇后， 使任意两个皇后都不能处于同一行、 同一列或同一斜线上。

搜索空间:N叉树

4后问题：解是一个4维向量， (x1, x2, x3, x4)（放置列号），这里x1为第一行，x2为第二行，以此类推。

搜索空间： 4叉树

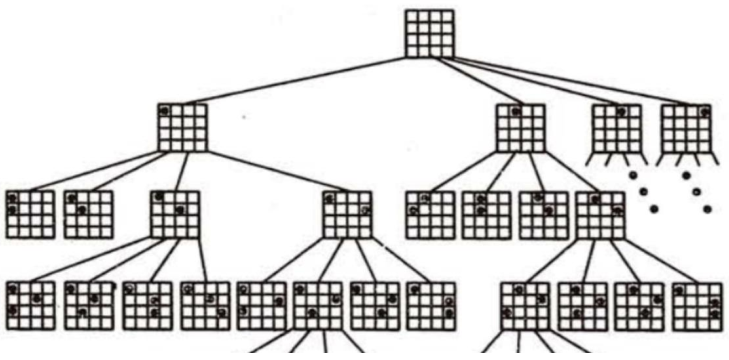
8后问题：解是一个8维向量， (x1, x2, x3, x4, x5, x6, x7, x8)

搜索空间： 8叉树,一个解： <1,3,5,2,4,6,8,7>

问题分析

确定问题状态： 问题的状态即棋盘的布局状态。

构造状态空间树： 状态空间树的根为空棋盘，每个布局的下一步可能布局是该布局结点的子结点。

由于可以预知，在每行中有且只有一个皇后，因此可采用逐行布局的方式，即每个布局有n个子结点

? 设4个皇后为xi， 分别在第i行(i=1， 2， 3， 4)；

? 问题的解状态：可以用(1, x1)， (2, x2)， ……， (4, x4)表示4个皇后的位置；

? 由于行号固定， 可简单记为： (x1, x2, x3, x4)；例如：(4, 2, 1, 3)

? 问题的解空间： (x1, x2, x3, x4)， 1≤xi≤4 (i=1， 2， 3， 4)， 共4! 个状态；

4皇后问题解空间的树结构

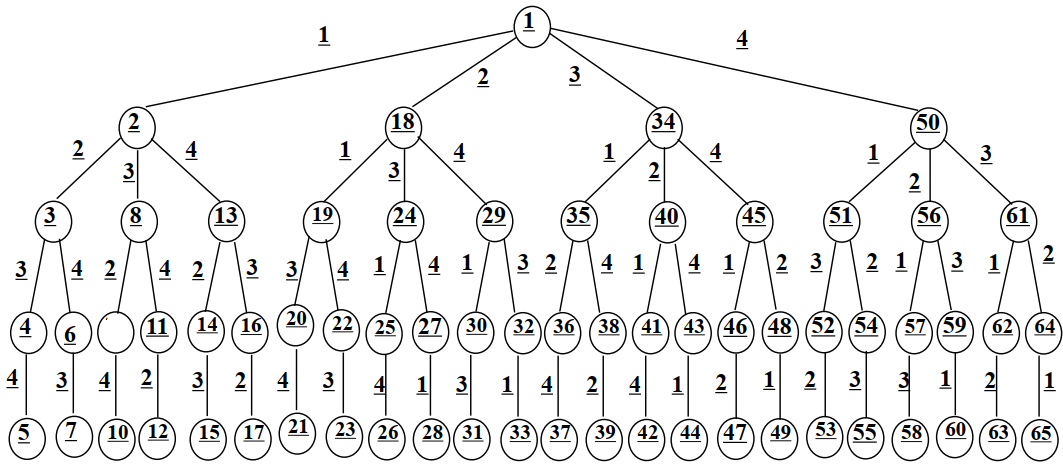
约束条件

? 任意两个皇后不能位于同一行上;

? 任意两个皇后不能位于同一列上，所以解向量X必须满足约束条件：

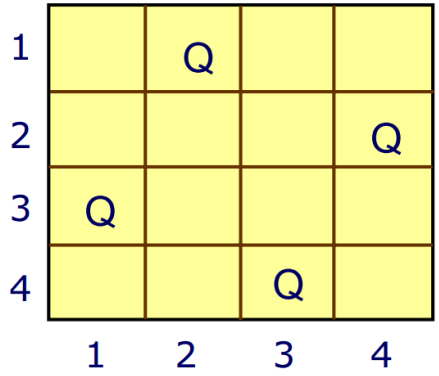
搜索解空间中进行剪枝

（1） 从空棋盘起， 逐行放置棋子。

（2） 每在一个布局中放下一个棋子， 即推演到一个新的布局。

（3） 如果当前行上没有可合法放置棋子的位置，则回溯到上一行， 重新布放上一行的棋子。

以4皇后问题为例

为了简化问题， 下面讨论4皇后问题。4皇后问题的解空间树是一个完全4叉树， 树的根结点表示搜索的初始状态， 从根结点到第2层结点对应皇后1在棋盘中第1行可能摆放的位置， 从第2层到第3层结点对应皇后2在棋盘中第2行的可能摆放的位置， 以此类推。

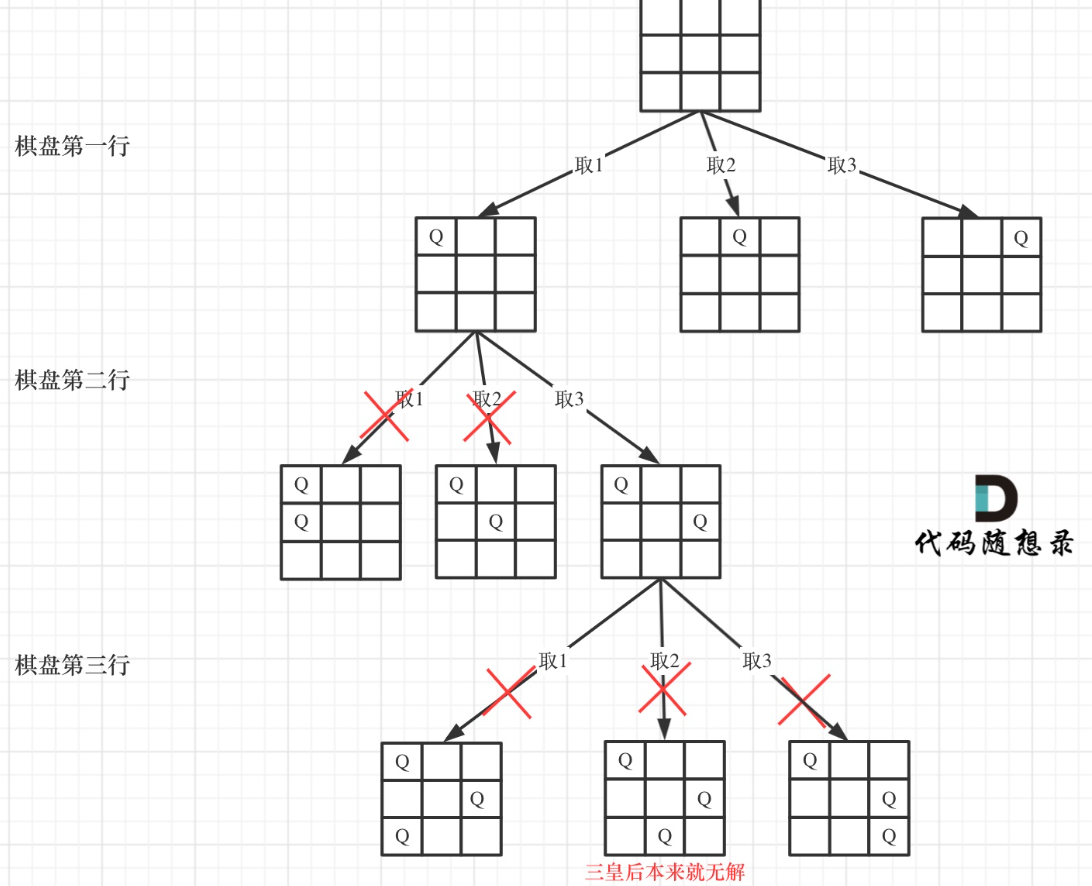
回溯法求解4皇后问题的搜索过程

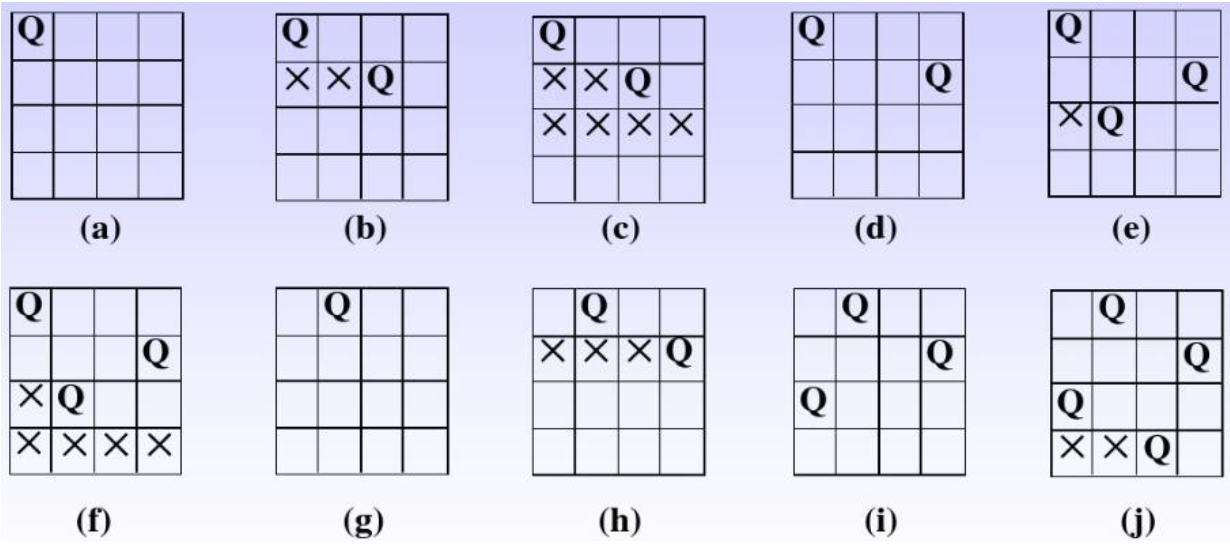
n=4的n皇后问题的搜索、 剪枝与回溯

代码思路

参考文章：代码随想录

回溯模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

递归终止条件

if (row == n) {
    result.push_back(chessboard);
    return;
}

单层搜索的逻辑

for (int col = 0; col < n; col++) {
    if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
        chessboard[row][col] = 'Q'; // 放置皇后
        backtracking(n, row + 1, chessboard);
        chessboard[row][col] = '.'; // 回溯，撤销皇后
    }
}

验证棋盘是否合法

按照如下标准去重：

不能同行(搜索过程从上到下自动解决了这个问题)

不能同列

不能同斜线 （45度和135度角）

实现代码与相关解释

package DaiMaSuiXiangLu;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class N_queen {
    //res用来存储可能的结果
    static List<List<String>> res = new ArrayList<>();

    public static void main(String[] args) {
        int n = 4;
        //画棋盘n*n
        char[][] chessboard = new char[n][n];
        for (char[] c : chessboard) {
            Arrays.fill(c, '.');
        }
        backTrack(n, 0, chessboard);
        for (int i = 0; i < res.size(); i++) {
            System.out.println("方案"+(i+1));
            for (int j = 0; j < res.get(i).size(); j++) {
                System.out.println(res.get(i).get(j));
            }
        }
    }

    /**
     * @param n          棋盘的大小
     * @param row        当初正在处理哪一行
     * @param chessboard 当前棋盘的状况
     */
    public static void backTrack(int n, int row, char[][] chessboard) {
        if (row == n) {
            //将结果赋给的新的list
            //这是因为List是引用类型，需要每次开辟新的空间给一个新的list来保存结果
            res.add(Array2List(chessboard));
            return;
        }
        for (int col = 0; col < n; ++col) {
            //剪枝操作,暴力点也可以不剪枝，对最后保存下来的多个结果去检查他们的合法性
            //尝试对该行的每一列放置皇后
            if (isValid(row, col, n, chessboard)) {
                chessboard[row][col] = 'Q';
                backTrack(n, row + 1, chessboard);
                chessboard[row][col] = '.';
            }
        }
    }
    //用于生成新的list
    public static List Array2List(char[][] chessboard) {
        List<String> list = new ArrayList<>();

        for (char[] c : chessboard) {
            list.add(String.copyValueOf(c));
        }
        return list;
    }

    /**
     *
     * @param row 当前递归是在row行,col列放置了一个新的皇后
     * @param col 当前递归是在row行,col列放置了一个新的皇后
     * @param n 棋盘大小
     * @param chessboard 当前棋盘的状况
     * @return 是否违背了合法性
     */
    public static boolean isValid(int row, int col, int n, char[][] chessboard) {
        //行无需检查,因为backTrack的递归保证了每一行只有一个皇后
        // 检查列
        for (int i = 0; i < row; ++i) { // 相当于剪枝
            if (chessboard[i][col] == 'Q') {
                return false;
            }
        }
        // 检查45度对角线
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        // 检查135度对角线
        for (int i = row - 1, j = col + 1; i >= 0 && j <= n - 1; i--, j++) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }

}