大数据HCIE成神之路之数据预处理（5）——偏态数据处理

1.1 偏态数据三种处理方案

1.1.1 实验背景

许多经典的统计方法和机器学习算法都假设数据服从正态分布，因为正态分布具有许多有用的性质。在数据预处理阶段会查看目标变量以及各个特征是否服从或接近正态分布，如果偏离就通过一定变换将该数据的分布正态化。

提问1：什么叫正态分布？
回答：正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution）。

提问2：什么叫偏态数据？
回答：偏态数据是指数据分布中存在明显的不对称性。正偏态表示尾部向右延伸，负偏态表示尾部向左延伸。了解偏态性对数据分析和建模很重要，可能需要数据转换或采样方法来处理。如下图所示，红色表示正态分布，黑色表示不同偏度，绿色和蓝色表示正负峰度。偏度（skewness）和峰度（Kurtosis）就是两个常见的统计量。

提问3：偏度的意义是什么？

• 实际数据很少遵循正态分布。而偏度衡量了数据分布的不对称性，对于了解数据分布的形状来说至关重要。
• 偏度告诉我们离群值的方向。正偏度表示存在较大的极值，负偏度表示存在较小的极值。
• 偏度可以揭示大多数值集中在哪里，以及反应了均值、中位数以及众数间的大小关系。

提问4：偏态数据有哪些处理方案

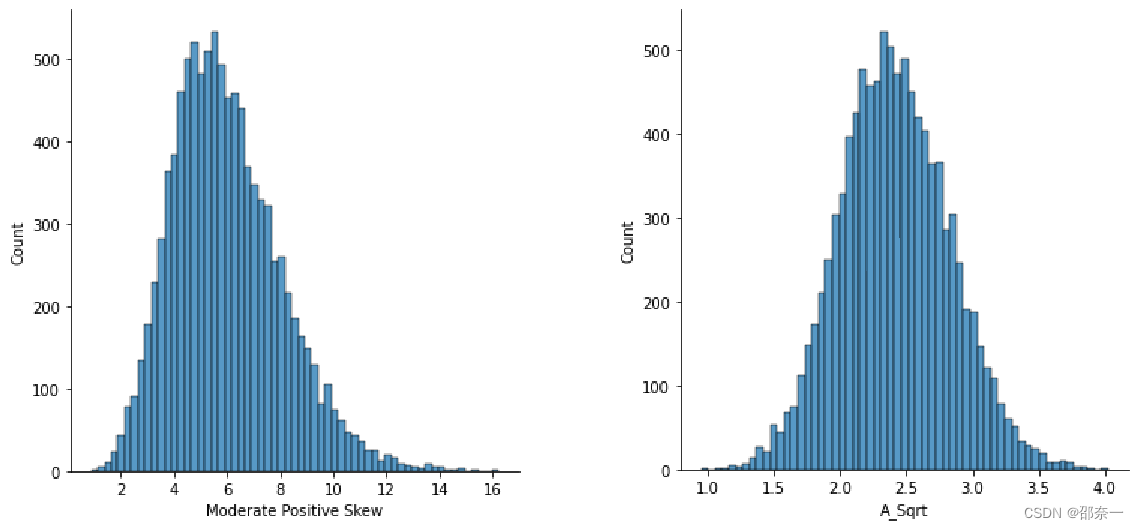
方案一：平方根法通常用于数据是中等偏斜的情况下。平方根sqrt(x)是一种对分布形状有适度影响的变换。它一般用于减少右偏的数据。平方根可以应用于零值，最常用于计数数据。左图与右图分别为使用平方根变换前后的分布图。

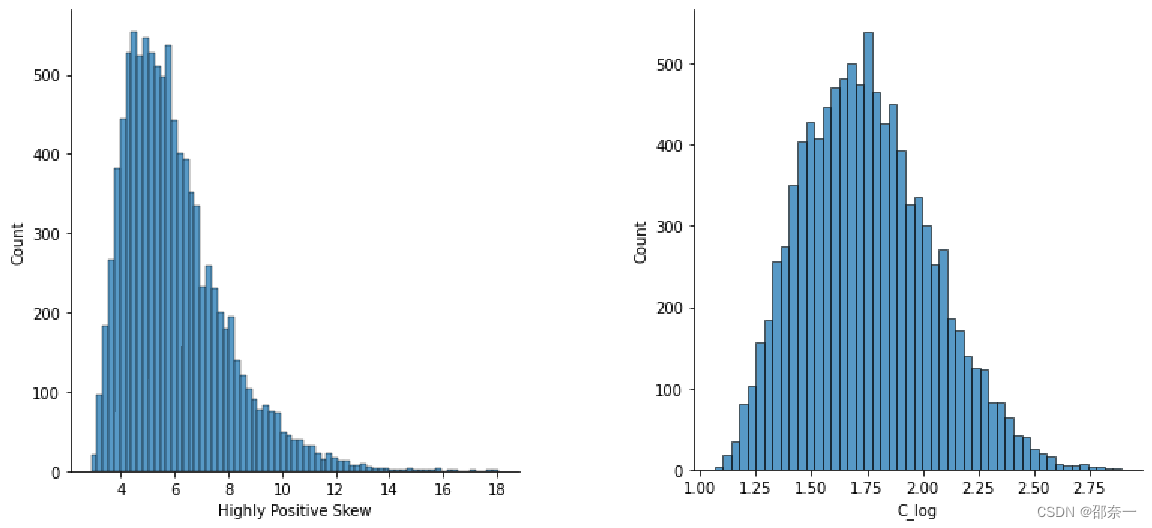
方案二：对数是一种强烈的变换，对分布形状有重大影响。这种技术和平方根法一样，经常用于减少右偏度。然而，它不能应用于零或负值。左图与右图分别为使用对数转换前后的分布图。

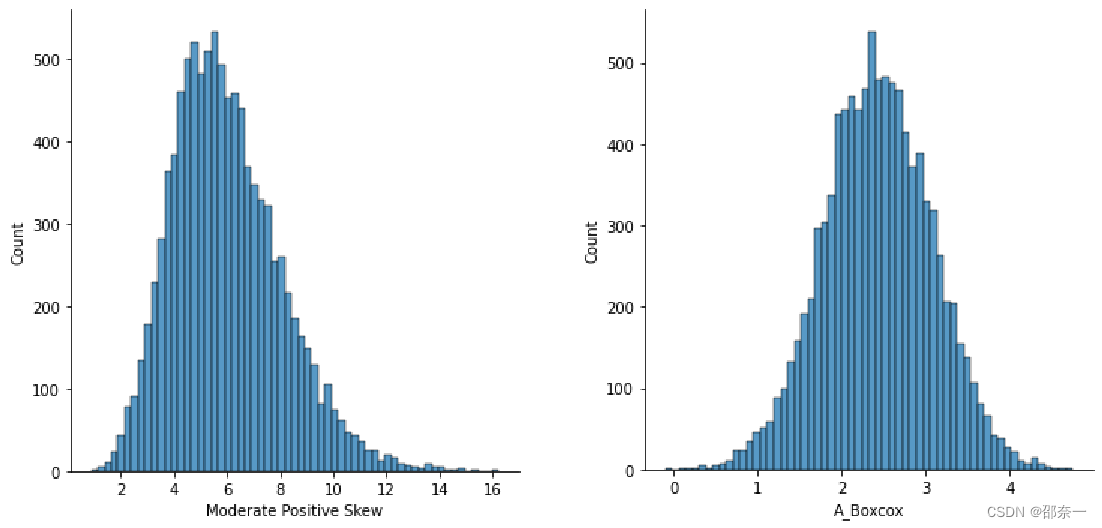
方案三：Box-Cox转换也是一种将非正态数据转换为正态的技术。 这是一个确定合适的指数（Lambda=l）的程序，用于转换偏斜数据。左图与右图分别为使用Box-Cox转换前后的分布图。经过对比，Box-Cox 变换比平方根法和对数变换的纠偏效果更好。

1.1.2 实验目标

利用开源的Data_to_Transform.csv数据集分别完成平方根法、对数转换法、Box-Cox转换法3个具体方法的练习。

1.1.3 实验数据解析

Data_to_Transform.csv 数据集来自开源网络，分别有4个特征表征数据分布的不同特点，中度正偏斜（右偏斜），高度正偏斜（右偏），中度负偏态（左偏态），高度负偏斜（左偏斜）。

数据的形式为：

Moderate Positive Skew,Highly Positive Skew,Moderate Negative Skew,Highly Negative Skew
0.8999903238341513,2.8950737861215154,11.1807475749096,9.027484717896854
1.113553800140345,2.9623848832717643,10.842938042093646,9.00976197446008
1.1568300607658637,2.9663775275342577,10.817933754084255,9.006134118699734
1.264130882866584,3.000323728370847,10.764569729078953,9.000125381390607
1.3239143362793078,3.012108870896731,10.753116852077191,8.98129613362068

Moderate Positive Skew：中度正偏斜
Highly Positive Skew：高度正偏斜
Moderate Negative Skew：中度负偏态
Highly Negative Skew：高度负偏斜

1.1.4 实验思路

通过python导入 Data_to_Transform.csv 数据集，对数据进行简单解读和整合后，通过调用平方根法，对数变换，Box-Cox对数据进行转换，对比前后变化，分析3种方法的区别。

1.1.5 实验操作步骤

步骤1 导入相关模块和 Data_to_Transform.csv 数据集

读取数据集：

import pandas as pd
import numpy as np
import seaborn as sns
# Reading dataset with skewed distributions
df = pd.read_csv('./data/Data_to_Transform.csv')
df.info()

稍等一小会，会输出结果：

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10000 entries, 0 to 9999
Data columns (total 4 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Moderate Positive Skew 10000 non-null float64
1 Highly Positive Skew 10000 non-null float64
2 Moderate Negative Skew 10000 non-null float64
3 Highly Negative Skew 10000 non-null float64
dtypes: float64(4)
memory usage: 312.6 KB

解释：如果报错没有seaborn库，则需要安装（不报错则跳过）。参考如下：

!pip install ./data/seaborn-0.12.2-py3-none-any.whl

该数据框架有10000行和4列，查看数据分布。

df.hist(grid=False,
	figsize=(10, 6),
	bins=30)

输出结果：

代码解释：

• df 是一个 DataFrame 对象，可能包含多个列。
• hist() 是 Pandas DataFrame 对象的函数，用于绘制直方图。
• grid=False 参数表示不显示直方图的网格线。
• figsize=(10, 6) 参数指定了绘图的尺寸，宽度为 10 英寸，高度为 6 英寸。
• bins=30 参数指定了直方图的柱子数量，这里设置为 30。

通过运行上述代码，将会绘制一个包含 DataFrame df 中所有列的直方图。每个列将会有一个独立的直方图，横轴表示数据的 取值范围 ，纵轴表示该取值范围内的 数据数量 。

该代码片段可用于快速查看数据的分布情况，帮助了解数据的形态、集中程度和离散程度等信息。直方图可以提供关于数据的大致分布情况，例如是否存在偏态、峰值集中程度等。

继续测量数据集中的峰度与偏度：

df.agg(['skew', 'kurtosis']).transpose()

输出结果：

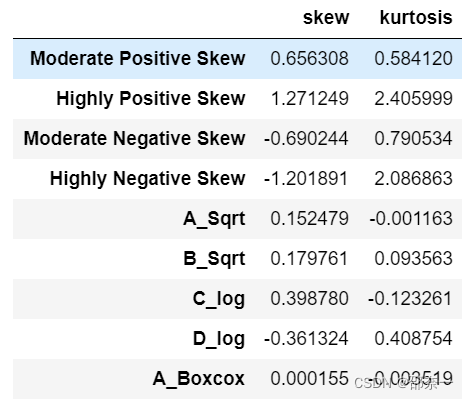
上述代码是对 DataFrame 对象进行聚合操作的示例代码。

• df 是一个 DataFrame 对象，可能包含多个列。
• agg() 是 Pandas DataFrame 对象的函数，用于对数据进行 聚合操作 。
• [‘skew’, ‘kurtosis’] 是作为参数传递给 agg() 函数的聚合函数列表。在这里，使用了两个聚合函数，分别是偏度（skewness）和峰度（kurtosis）。注意不能写错，否则会报错。比如将 skew 写成 skewness ，则包报错： 'skewness' is not a valid function for 'Series' object .
• transpose() 是对结果进行转置操作，将行和列进行互换，使得结果更易读。

通过运行上述代码，将会计算 DataFrame df 中每一列的偏度和峰度，并将结果以 DataFrame 的形式返回。每一行表示一个列，每一列表示一个聚合函数。

• 偏度（skewness）是描述数据分布 偏斜程度 的统计量。正偏态数据的偏度大于零，表示数据分布右偏；负偏态数据的偏度小于零，表示数据分布左偏；偏度接近零则表示数据分布接近对称。
• 峰度（kurtosis）是描述数据分布 峰态 的统计量。正态分布的峰度为3，称为 正常峰度 。高于3的峰度表示数据分布比正态分布更陡峭（尖峰），低于3的峰度表示数据分布比正态分布更平坦。

提问：正态分布的峰度一定是3吗？
回答：在标准正态分布（均值为0，标准差为1）中，峰度的确刚好为3。这种情况下，我们称之为 “正常峰度”。

步骤2 平方根法

查看第一列正偏斜原始分布。

sns.displot(df.iloc[:, 0])

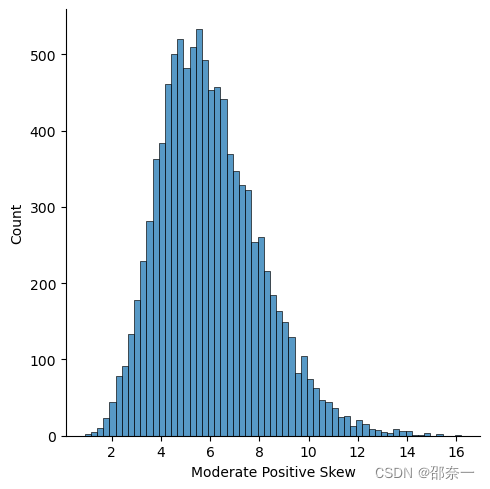
解释：displot() 是 seaborn 库的函数，用于绘制分布图。

运用平方根法对第一列正偏斜进行转换，并查看转换后的分布。

df.insert(len(df.columns), 'A_Sqrt',
np.sqrt(df.iloc[:,0]))
sns.displot(df.loc[:,'A_Sqrt'])

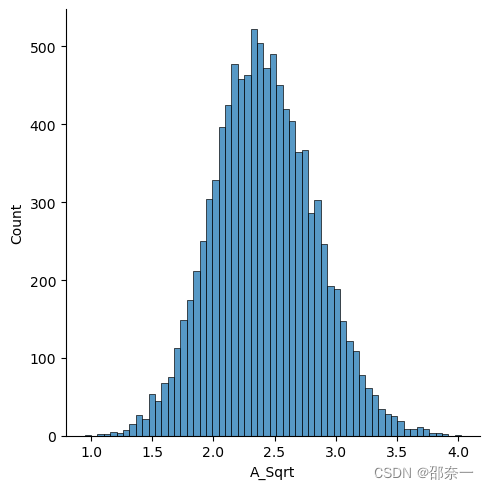
解释：补充学习insert方法

import pandas as pd

# 创建一个示例DataFrame
data = {'Name': ['John', 'Emma', 'Mike'],
        'Age': [25, 28, 32],
        'City': ['New York', 'London', 'Paris']}
df = pd.DataFrame(data)
print("初始DataFrame:")
print(df)

输出结果：

初始DataFrame:
   Name  Age      City
0  John   25  New York
1  Emma   28    London
2  Mike   32     Paris

现在，我们将在索引位置为1的位置插入一个新的列"Salary"，并为每个行指定相应的值。

# 使用insert方法插入新的列
df.insert(1, "Salary", [5000, 6000, 7000])
print("\n插入新列后的DataFrame:")
print(df)

输出结果：

插入新列后的DataFrame:
   Name  Salary  Age      City
0  John    5000   25  New York
1  Emma    6000   28    London
2  Mike    7000   32     Paris

在上述代码中，我们使用insert方法将新的列"Salary"插入到索引位置1。第一个参数是插入位置的索引，第二个参数是新列的名称，第三个参数是一个列表，包含了要插入的每个行的值。

查看第三列负偏斜数据。

sns.displot(df.iloc[:,2])

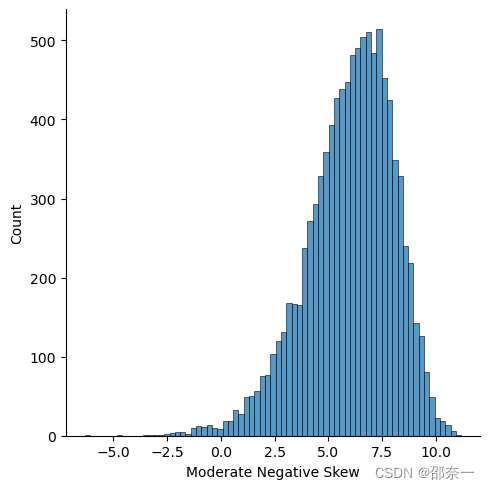
注意：此处的写法是 df.iloc[] ;

平方根方法来转换负（左）倾斜的数据。

df.insert(len(df.columns), 'B_Sqrt',
np.sqrt(max(df.iloc[:, 2]+1) - df.iloc[:, 2]))
sns.displot(df.loc[:,'B_Sqrt'])

思考：为什么要计算第三列元素与该列最大值之间的差值的平方根？目的是什么？
答案：计算第三列元素与该列最大值之间的差值的平方根的目的可能是为了进行数据的标准化或者变换，以探索数据的分布特征或进行数据预处理。常见的数据标准化方法之一是使用 Z-score 标准化，即将数据转换为均值为0，标准差为1的标准正态分布。通过计算差值的平方根，可以对数据进行一种线性变换，使得数据更接近于标准正态分布的形态，同时保留了差值的相对大小关系。

思考2： np.sqrt(max(df.iloc[:, 2]+1) - df.iloc[:, 2])) 这句代码中为什么是+1而不是+2？
答案：

1. 如果在 max(df.iloc[:, 2]+1) 中没有添加 +1，并且第三列中的最大值为0，那么计算结果将为负无穷大（-inf），因为 sqrt(0 - 0) 的结果为0。
2. 但是，如果我们在 max(df.iloc[:, 2]+1) 中添加了 +1，则即使第三列中的最大值为0，计算结果仍为1，即 sqrt(1 - 0) 的结果为1。

通过添加 +1，可以确保在计算平方根之前，差值至少为1，避免了零除错误和负无穷大的结果。
你也可以尝试直接开平方，但是效果不好。

步骤3 对数转换

查看高度正偏数据分布。

sns.displot(df.loc[:,'Highly Positive Skew'])

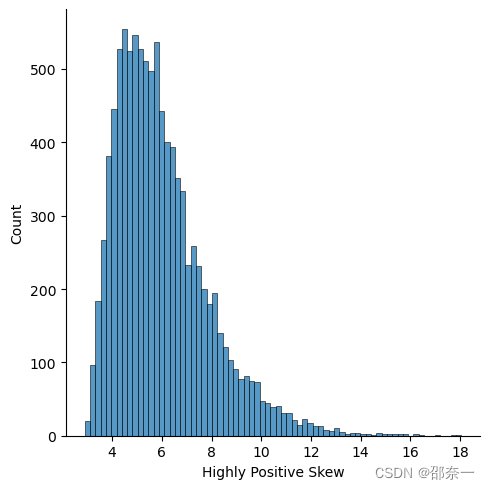
对高度正偏数据进行对数转换，并查看转换后的数据分布。

# Python log transform
df.insert(len(df.columns), 'C_log',
np.log(df['Highly Positive Skew']))
sns.displot(df.loc[:,'C_log'])

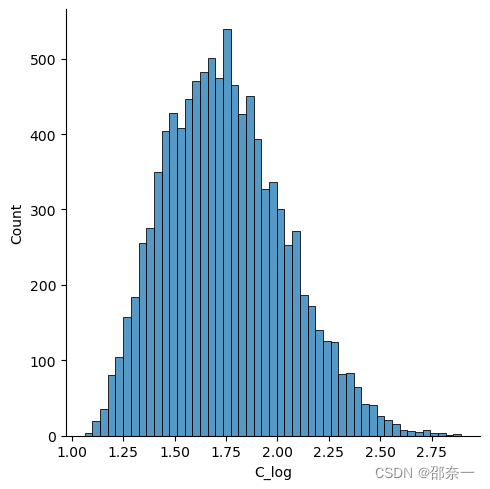
对高度负偏数据进行对数转换，并查看转换后的数据分布。

df.insert(len(df.columns), 'D_log',
np.log(max(df.iloc[:, 2] + 1) - df.iloc[:, 2]))
sns.displot(df.loc[:,'D_log'])

步骤4 Box-Cox转换

查看第一列数据分布。

sns.displot(df.iloc[:,0])

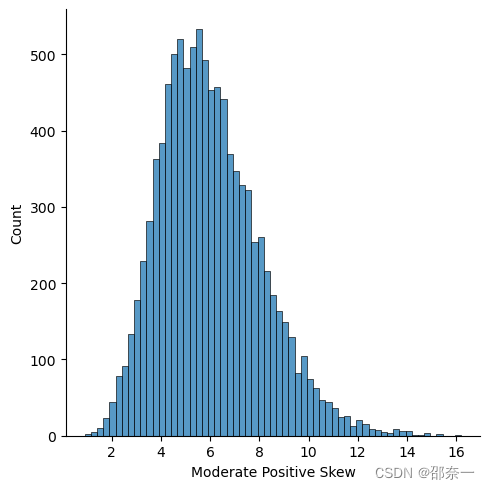
对第一列数据进行boxcox转换，并查看转换后的数据分布。

from scipy.stats import boxcox
df.insert(len(df.columns), 'A_Boxcox',
boxcox(df.iloc[:, 0])[0])
sns.displot(df.loc[:,'A_Boxcox'])

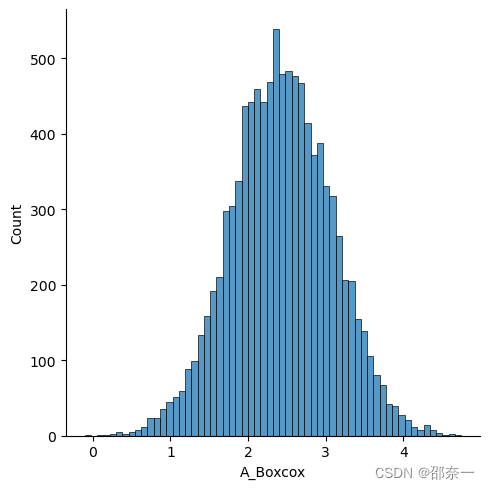
查看所有列的偏度。

df.agg(['skew']).transpose()