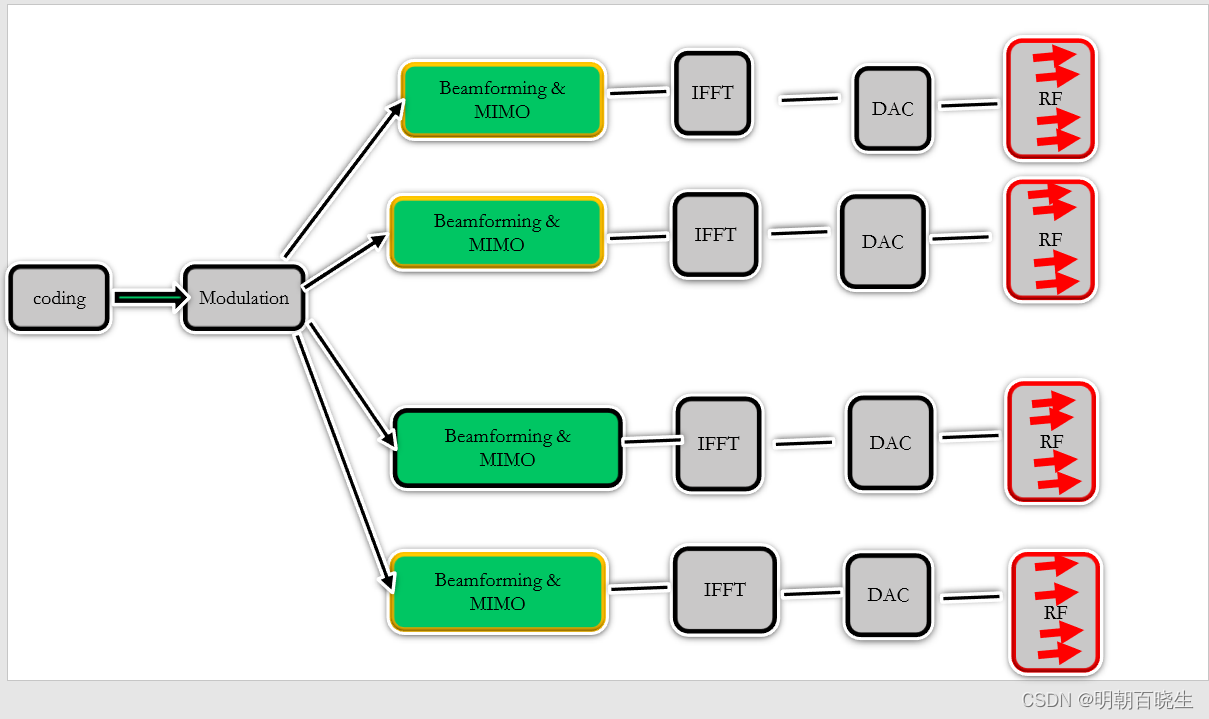
【MIMO 从入门到精通】[P4]【MIMO Communications】

发布时间：2023年12月25日

前言：

? ??Explains the main approaches to multi-input multi-output (MIMO) communications, including Beamforming, Zero Forcing, and MMSE. * Note that at the 9:19min mark, I made a slight "voice typo", where I should have said: "you need to tell the transmitter what the channel is" (not the receiver), and this also holds for the SVD approach too which I should have mentioned. Check out my 'search for signals in everyday life', by following my social media feeds:

?

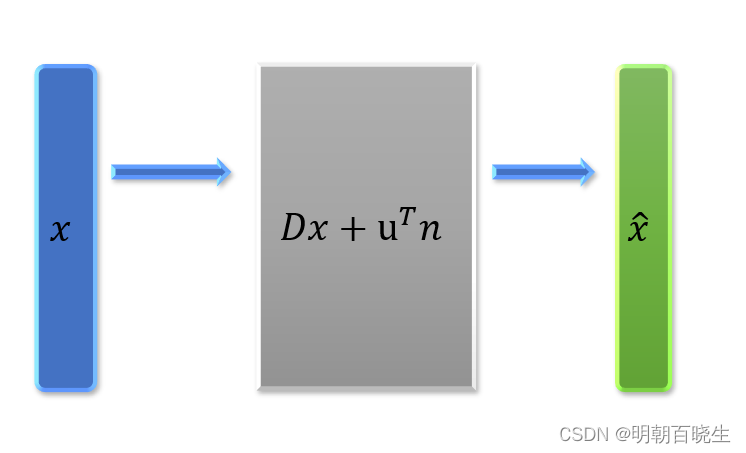
MIMO 系统发送符号为x, 接收到的符号为y,噪声?n

?y=Hx+n

接收方如何解码出\hat{x},本章重点介绍相关的解码方案

目录：

  1. ? Z.F.receiver
  2. ? MMSE receiver
  3. ? Z.F precoder
  4. ? SVD?receiver
  5. ? Beamforming 跟 MIMO 关系

??

一? Z.F.receiver

? ?Zero Forcing receiver

? ? ??\hat{x}=H^{-}y

? ? ? ? ?=H^{-}(Hx+n)

? ? ? ? ?=x+H^{-}n

? ? 该解码方案优点：

? ? ? ? ? ?简单，当噪声很小的时候, 估计值接近真实值x

? ? ? 缺点：

? ? ? ? ? ?当噪声很大的时候，相差较大

? ? ? ? ? ?当noise amplificationH^{-}是非满秩矩阵的时候，相当于一个噪声信号放大器noise amplification

。

? ? ? ? ? 考虑scalar场景：?比如H=0,则其逆为无穷大

二? MMSE receiver

? ??\hat{x}=(H^TH)^{-}(H^Ty)

? ?原理：建议看一下机器学习的回归算法是

? 我们已知y,H.要求x，就是要使得下面的损失函数最小值

??l= argmin_{x}||Hx-y||^2

?就是求微分，使得损失函数最小,利用向量链式法则（参考下面连接：矩阵求导术）

??H^T(Hx-y)=0

?H^THx=H^Ty

\hat{x}=(H^TH)^{-}H^Ty

为了防止过拟合，L2正规化 ,也可以防止H^TH不可逆

? ??l= argmin_{x}||Hx+\sigma^2x-y||^2

? ? ?\hat{x}=(H^TH+\sigma^2I)^{-}H^Ty

?三? Z.F precoder

当发送方通过接收方反馈,知道H的时候,先求出逆矩阵

发送符号：

? ? ? ? ? ? ???x=H^{-}x

接收符号:

? ? ? ? ? ? ??\hat{x}=y=H(H^{-}x)+n=x+n

? ?优点：

? ?针对noise，没有noise amplificationH^{-}

? ?缺点：

? ? 需要通过反馈 ，通知发送方H

四? SVD?receiver

? ? ? ? ?singlular value decomposition

? ? ? ? ?H=uDv^T（u,v 是正交矩阵）

? ? ? ? ?发送符号：

? ? ? ? ? ?x=vx

? ? ? ? 接收的符号

? ? ? ? ? ?y=Hvx+n

? ? ? ? ? 解码

? ? ? ? ?\hat{x}=U^Ty

? ? ? ? ? ? ?=u^TuDv^Tvx+u^Tn(利用正交性）

? ? ? ? ? ? ? ?=Dx+u^Tn

? ? ? ? ?

?正交矩阵

?UU^T=E

VV^T=E

D:? 对角矩阵，由对称矩阵 HH^T或 H^TH的特征值的开平方组成，称为奇异值（从大到小排列，U和V对应的特征向量亦如此）

? 五? Beamforming 跟 MIMO 关系

? ? ? ?前面讲过通过SVD receiver

? ? ??

? ? ? ?\hat{x}=Dx+u^Tn

? ? ?diffrent sub channels different powers

? ? ?当 SNR 很高的时候：发送x的时候使用相同的power： p

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??x=px:? p代表功率放大倍数

? ? ?当SNR 很低的时候：?

? ? ? ? ? ?前面x 是一个向量?x=\begin{bmatrix} x_1\\ x_2 \\ .. \\ x_n \end{bmatrix}

? ? ? ? ? 我们选择出SNR 最好的那一路?x_j,发送?vx_j

? ? ? ? ?接收到的信号

? ? ? ? ? ? ? ? ? ?\hat{x}=u^TH(vx_j)+u^Tn

? ? ? ? ? ? ? ? ? ? ? ??=Dx_j +u^Tn

? ? ? ? ? ? ? ? ? ? ? ? ?

参考：

回归算法：?CSDN

矩阵求导术： CSDN

特征值和特征向量 - 知乎

文章来源:https://blog.csdn.net/chengxf2/article/details/135078547
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章