从费舍尔信息矩阵(Fisher Information Matrix, FIM)到自然梯度法
文章目录
0. Preliminary
- 考虑一个机器学习模型的训练过程。模型本身常常设计为参数化概率模型
p
(
x
∣
θ
)
p(x|\pmb{\theta})
p(x∣θ),通过优化损失函数
L
\mathcal{L}
L 的方式最大化模型表示的似然函数,从而拟合数据中的映射关系。由于似然函数本身是一个概率分布,当参数从
θ
\pmb{\theta}
θ 更新为
θ
+
d
\pmb{\theta} + \pmb{d}
θ+d 时,可以用 KL 散度
K
L
[
p
(
x
∣
θ
)
∥
p
(
x
∣
θ
+
d
)
]
\mathrm{KL}[p(x|\pmb{\theta}) \| p(x|\pmb{\theta}+\pmb{d})]
KL[p(x∣θ)∥p(x∣θ+d)] 来度量模型所描述的映射关系的变化程度。这里存在两个空间
分布空间:模型似然 p ( x ∣ θ ) p(x|\pmb{\theta}) p(x∣θ) 取值的空间。可以用 KL 散度度量其中任意两点之间的差异程度参数空间:参数向量 θ \pmb{\theta} θ 取值的空间。由于许多机器学习模型 p ( x ∣ θ ) p(x|\pmb{\theta}) p(x∣θ) 在参数空间中可能会表现出较为光滑的性质,即 d → 0 \pmb{d}\to\pmb{0} d→0 时 K L [ p ( x ∣ θ ) ∥ p ( x ∣ θ + d ) ] → 0 \mathrm{KL}[p(x|\pmb{\theta}) \| p(x|\pmb{\theta}+\pmb{d})] \to 0 KL[p(x∣θ)∥p(x∣θ+d)]→0,这使参数空间往往具有某种流形结构,即在宏观上存在曲率,但在局部上类似于欧几里得空间。
- 观察一下常规梯度下降更新公式
θ k + 1 ← θ k ? α ▽ θ L ( θ k ) \pmb{\theta}_{k+1} \leftarrow \pmb{\theta}_k - \alpha \triangledown_{\pmb{\theta}} \mathcal{L}(\pmb{\theta}_k) θk+1?←θk??α▽θ?L(θk?) 注意到参数更新方向由梯度 ? ▽ θ L ( θ k ) -\triangledown_{\pmb{\theta}} \mathcal{L}(\pmb{\theta}_k) ?▽θ?L(θk?) 给出,这是参数空间中在 θ k \pmb{\theta}_k θk? 局部最陡峭的下降方向,形式化地表示为
? ? θ L ( θ ) ∥ ? θ L ( θ ) ∥ = lim ? ? → 0 1 ? arg ? min ? d ?s.t.? ∥ d ∥ ≤ ? L ( θ + d ) \frac{-\nabla_{\pmb{\theta}} \mathcal{L}(\pmb{\theta})}{\left\|\nabla_{\pmb{\theta}} \mathcal{L}(\pmb{\theta})\right\|}=\lim _{\epsilon \rightarrow 0} \frac{1}{\epsilon} \underset{\pmb{d} \text { s.t. }\|\pmb{d}\| \leq \epsilon}{\arg \min } \mathcal{L}(\pmb{\theta}+\pmb{d}) ∥?θ?L(θ)∥??θ?L(θ)?=?→0lim??1?d?s.t.?∥d∥≤?argmin?L(θ+d) 上式说明:参数空间中最陡的下降方向 d \pmb{d} d 满足新参数 θ + d \pmb{\theta}+\pmb{d} θ+d 在当前参数 θ \pmb{\theta} θ 的 ? \epsilon ? 邻域内,且能最小化损失函数 L \mathcal{L} L。由于梯度下降法中参数的邻域是通过欧氏范数(L2范数)刻画的,因此梯度下降优化过程依赖于 θ \theta θ 参数空间中的欧氏度量 梯度下降法 (Gradient descent)将参数空间视作一种欧氏空间,梯度向量是通过对目标函数在当前点进行一阶泰勒展开得到的。这样的线性逼近在局部范围内是合理的,但由于欧氏空间不存在曲率,在高度非线性或弯曲的参数空间中,其可能不足以准确描述整个参数空间的结构,导致梯度下降过程收敛缓慢或出现震荡。自然梯度法 (Natural Gradient Descent)将参数空间视为黎曼空间中的一个黎曼流形,这样就能在优化过程中考虑到参数空间的曲率,以缓解梯度下降法的收敛问题。该方法主要借助费舍尔信息矩阵 (Fisher Information Matrix, FIM)的逆度量参数空间的几何机构和曲率信息,通过适当的度量调整梯度的方向实现更好的优化过程- 本文以自然梯度法为脉络,贯穿以下概念
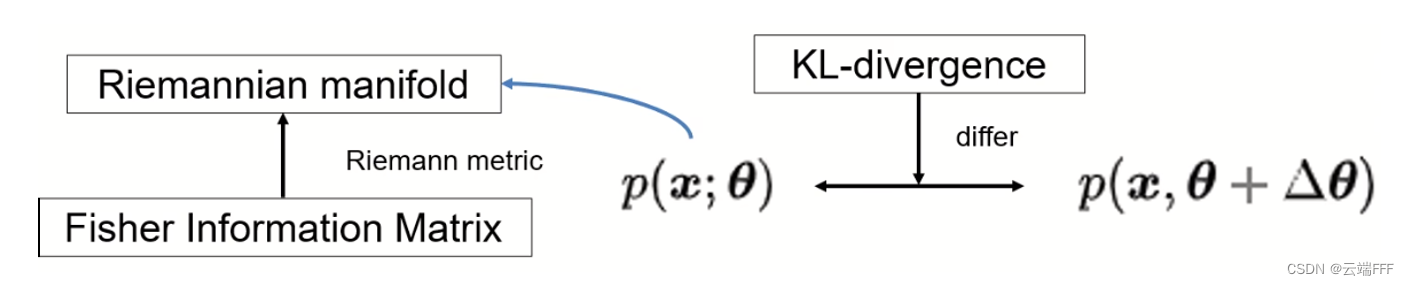
-
θ
\theta
θ 的参数空间可以一个
黎曼流形 (Riemannian manifold) - 黎曼流形是一种特殊的
黎曼空间 (Riemannian space) - 黎曼空间是一种完备的内积空间,其内积结构称为
黎曼度量 (riemannian metric) 费舍尔信息矩阵 (Fisher Information Matrix, FIM)是一种特殊的黎曼度量,它本身度量了参数空间中的曲率,描述了似然函数对参数的敏感性KL散度 (KL-divergence)的二阶泰勒展开形式与 FIM 相关,利用 FIM 可以得到一种常用的 KL 散度近似方法- FIM 是对数似然函数的
海森矩阵 (Hessian Matrix)H log ? p ( x ∣ θ ) \mathrm{H}_{\log p(x|\theta)} Hlogp(x∣θ)? 的期望的负值,可以看作对数似然函数 log ? p ( x ∣ θ ) \log p(x|\theta) logp(x∣θ) 的曲率的度量 - 利用 FIM 提供的参数空间曲率信息调整梯度下降法的更新过程,即得到
自然梯度法 (Natural Gradient Descent)
-
θ
\theta
θ 的参数空间可以一个
1. 黎曼空间与黎曼流形
1.1 黎曼空间
-
黎曼空间 (Riemannian space)是一种以黎曼度量作为内积结构的,完备的内积空间- 内积空间:是定义了内积操作的向量空间,基于内积运算,可以定义向量元素的长度(范数)和元素之间的夹角等概念,进而可在空间中建立交角、垂直和投影等欧几里得几何学。习惯上称二维或三维的内积空间为欧氏空间,内积空间是欧氏空间的推广
- 黎曼度量:是一种定义在流形上的光滑的内积结构,用于度量流形上切空间中向量的长度和角度(详见 1.2 节)
- 完备:是指空间中没有任何遗漏的点,就是说该空间中任何一个点,在与它的距离趋近为 0 的地方都存在另一个同属于该空间的点。完备性意味着该空间对极限操作封闭
-
黎曼空间中曲面的表示形式比较简单,因而适用于解决曲面问题。如下图所示,相同的一个三维球体,在黎曼空间中的解析式比欧氏空间中简单很多

-
关于函数空间的更多说明,参考 函数空间一览:从线性空间到再生核希尔伯特空间
1.2 黎曼流形
流形 (manifold)是一种数学概念,用于描述一种特殊的拓扑空间:流形上任意一点的局部都具有欧几里德空间的拓扑结构(与欧几里德空间同胚),即每个点都有一个邻域,可以通过光滑的映射与欧几里德空间的开集一一对应。这种局部同胚性质使得我们能够在流形上引入欧几里德空间中的概念,如切空间、切向量、长度、夹角等。以下是一个流形的示意图,它从整体上看可以具有复杂的光滑或非光滑曲面结构,但是在任意局部和欧氏空间同构

黎曼流形 (Riemannian manifold)是黎曼空间中的流形,是一种引入了黎曼度量的流形切空间 (Tangent space)指流形上任意点 p p p 处的线性近似空间,记为 T p M T_pM Tp?M黎曼度量 (riemannian metric)定义了切空间上的内积运算。设 M M M 是一个流形,对于其上的每个切空间,黎曼度量 g g g 定义了
g p ( v , w ) , v , w ∈ T p M g_p(v,w), \quad v,w\in T_pM gp?(v,w),v,w∈Tp?M该内积运算满足以下性质
对称性 : g ( v , w ) = g ( w , v ) 正定性 : ? v ∈ T p M , ? g ( v , v ) > 0 线性性 : g ( a v + b w , u ) = a ? g ( v , u ) + b ? g ( w , u ) , ?其中 a , b 是标量 光滑性 : 在局部坐标系下,内积结构? g ?的各个分量是光滑函数 \begin{aligned} &对称性: &&g(v,w)=g(w,v) \\ &正定性: &&\forall v\in T_pM,\space g(v,v) > 0\\ &线性性: &&g(av+bw,u) = a·g(v,u) + b·g(w,u), \space 其中 a,b 是标量\\ &光滑性: && 在局部坐标系下,内积结构\space g\space 的各个分量是光滑函数 \end{aligned} ?对称性:正定性:线性性:光滑性:??g(v,w)=g(w,v)?v∈Tp?M,?g(v,v)>0g(av+bw,u)=a?g(v,u)+b?g(w,u),?其中a,b是标量在局部坐标系下,内积结构?g?的各个分量是光滑函数? 前三条性质确保了黎曼度量在切空间中表现为合法的内积结构,使得我们能够在流形上定义类似于欧几里德空间中的内积和度量的概念;最后一条确保了流形上定义的几何结构在局部是光滑的,即在流形上每一点处的切空间中的内积结构都可以通过局部坐标系的选择表示为光滑函数,而这些光滑函数在流形上是连续可微的
2. 海森矩阵、费舍尔信息矩阵和 KL 散度
2.1 海森矩阵
海森矩阵 (Hessian Matrix)是由某个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。形式化地说,对于 R n → R \mathbb{R}^n\to\mathbb{R} Rn→R 的多元实值函数 f ( x 1 , x 2 , ? ? , x n ) f\left(x_{1}, x_{2}, \cdots, x_{n}\right) f(x1?,x2?,?,xn?),其在 x \pmb{x} x 点处的 Hessian 矩阵定义为
H f ( x ) = [ ? 2 f ? x 1 2 ? f ? x 1 ? x 2 ? ? f ? x 1 ? x n ? 2 f ? x 2 ? x 1 ? f ? x 2 2 ? ? f ? x 2 ? x n ? ? ? ? ? 2 f ? x n ? x 1 ? f ? x n ? x 2 ? ? f ? x n 2 ] n × n \begin{array}{c} \mathrm{H}_f(\boldsymbol{x})=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{f}}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{f}}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{f}}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{f}}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{f}}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{f}}{\partial x_{n}^{2}} \end{array}\right]_{n\times n} \end{array} Hf?(x)= ??x12??2f??x2??x1??2f???xn??x1??2f???x1??x2??f??x22??f???xn??x2??f????????x1??xn??f??x2??xn??f???xn2??f?? ?n×n?? 要求 f f f 在展开位置 x x x 附近二阶连续可导(二阶偏导数连续,原函数光滑),由于二阶偏导数可交换, H f \mathrm{H}_f Hf? 是对称矩阵- 海森矩阵包含了函数的局部曲率信息,其作用包括
- 判断多元函数的极值问题
- 多元函数在某点的泰勒展开式的矩阵形式中,展开到二阶时就会出现 Hessian 矩阵
- 优化问题中,海森矩阵常常用于描述目标函数(损失函数)在某个点附近的二阶行为,从而可以帮助确定最优化算法的步长和方向,在牛顿法(Newton’s method)和拟牛顿法(Quasi-Newton methods)中都有用到
2.2 费舍尔信息矩阵
2.2.1 定义
-
考虑极大似然估计的过程,目标分布由 θ m × 1 = [ θ 1 , θ 2 , . . . , θ m ] T \pmb{\theta}_{m\times 1}=[\theta_1,\theta_2,...,\theta_m]^T θm×1?=[θ1?,θ2?,...,θm?]T 参数化,首先从目标分布中收集样本 x i ~ p ( x ∣ θ ) x_i \sim p(x|\pmb{\theta}) xi?~p(x∣θ) 构成数据集 X = { x 1 , x 2 , . . . , x n } \pmb{X} = \{x_1,x_2,...,x_n\} X={x1?,x2?,...,xn?},记为 X ~ p ( X ∣ θ ) \pmb{X}\sim p(\pmb{X}|\pmb{\theta}) X~p(X∣θ),然后写出对数似然函数
L ( X ∣ θ ) = ∑ i = 1 n log ? p ( x i ∣ θ ) L(\pmb{X}|\pmb{\theta}) = \sum_{i=1}^n \log p(x_i|\pmb{\theta}) L(X∣θ)=i=1∑n?logp(xi?∣θ) 通过最大化对数似然函数来得到估计参数,即
θ ^ = arg?max ? θ ∑ i = 1 n log ? p ( x i ∣ θ ) \hat{\pmb{\theta}} = \argmax_\theta \sum_{i=1}^n \log p(x_i|\pmb{\theta}) θ^=θargmax?i=1∑n?logp(xi?∣θ) 在取得极值处,应该有梯度为 0,即
▽ θ L ( X ∣ θ ) = ∑ i = 1 n ▽ θ log ? p ( x i ∣ θ ) ▽ θ L ( X ∣ θ ) ∣ θ = θ ^ = 0 \begin{aligned} & \triangledown _\theta L(\pmb{X}|\pmb{\theta}) = \sum_{i=1}^n \triangledown _\theta \log p(x_i|\pmb{\theta}) \\ & \triangledown _\theta L(\pmb{X}|\pmb{\theta})\big\vert_{\theta=\hat{\theta}} = \pmb{0} \end{aligned} ?▽θ?L(X∣θ)=i=1∑n?▽θ?logp(xi?∣θ)▽θ?L(X∣θ) ?θ=θ^?=0? -
基于以上观察,我们将关于任意样本 x x x 的对数似然函数的梯度定义为
得分函数 (score function),利用它评估 θ ^ \hat{\pmb{\theta}} θ^ 估计的良好程度
s ( x ∣ θ ) m × 1 = ▽ θ L ( x ∣ θ ) = ▽ θ log ? p ( x ∣ θ ) s(x|\pmb{\theta})_{m\times 1} = \triangledown _\theta L(x|\pmb{\theta})= \triangledown _\theta \log p(x|\pmb{\theta}) s(x∣θ)m×1?=▽θ?L(x∣θ)=▽θ?logp(x∣θ) 注意得分函数是标量对向量 θ \pmb{\theta} θ 求导,因此 s ( x ∣ θ ) s(x|\pmb{\theta}) s(x∣θ) 是和 θ \pmb{\theta} θ 相同尺寸的向量。得分函数的重要性质是其期望为 0,即 E x ~ p ( x ∣ θ ) [ s ( x ∣ θ ) ] = 0 \mathbb{E}_{x\sim p(x|\pmb{\theta})}\left[ s(x|\pmb{\theta})\right]=\pmb{0} Ex~p(x∣θ)?[s(x∣θ)]=0,证明如下E p ( x ∣ θ ) [ s ( x ∣ θ ) ] = E p ( x ∣ θ ) [ ? log ? p ( x ∣ θ ) ] = ∫ ? log ? p ( x ∣ θ ) p ( x ∣ θ ) d x = ∫ ? p ( x ∣ θ ) p ( x ∣ θ ) p ( x ∣ θ ) d x = ∫ ? p ( x ∣ θ ) d x = ? ∫ p ( x ∣ θ ) d x = ? 1 = 0 m × 1 \begin{aligned} \underset{p(x| \pmb{\theta})}{\mathbb{E}}[s(x|\pmb{\theta})] & =\underset{p(x |\pmb{\theta})}{\mathbb{E}}[\nabla \log p(x |\pmb{\theta})] \\ & =\int \nabla \log p(x |\pmb{\theta}) p(x |\pmb{\theta}) \mathrm{d} x \\ & =\int \frac{\nabla p(x |\pmb{\theta})}{p(x |\pmb{\theta})} p(x |\pmb{\theta}) \mathrm{d} x \\ & =\int \nabla p(x |\pmb{\theta}) \mathrm{d} x \\ & =\nabla \int p(x |\pmb{\theta}) \mathrm{d} x \\ & =\nabla 1 \\ & =\pmb{0}_{m\times 1} \end{aligned} p(x∣θ)E?[s(x∣θ)]?=p(x∣θ)E?[?logp(x∣θ)]=∫?logp(x∣θ)p(x∣θ)dx=∫p(x∣θ)?p(x∣θ)?p(x∣θ)dx=∫?p(x∣θ)dx=?∫p(x∣θ)dx=?1=0m×1??
因此可以用大量样本的 s ( x ∣ θ ) s(x|\pmb{\theta}) s(x∣θ) 期望评估参数估计值 θ ^ \hat{\pmb{\theta}} θ^ 的质量,即 E p ( x ∣ θ ) [ s ( x ∣ θ ^ ) ] \mathbb{E}_{p(x|\pmb{\theta})}\left[ s(x|\hat{\pmb{\theta}})\right] Ep(x∣θ)?[s(x∣θ^)] 越接近 0 \pmb{0} 0,估计越准确
-
进一步地,参数估计值 θ ^ \hat{\pmb{\theta}} θ^ 的置信度可以由大量样本的 s ( x ∣ θ ) s(x|\pmb{\theta}) s(x∣θ) 协方差来描述,这是一个围绕期望值的不确定度的度量,将以上期望为 0 的结果代入协方差计算公式,得到
E p ( x ∣ θ ) [ ( s ( x ∣ θ ) ? 0 ) ? ( s ( x ∣ θ ) ? 0 ) T ] \underset{p(x| \pmb{\theta})}{\mathbb{E}}[\left(s(x|\pmb{\theta})-\pmb{0}\right)·\left(s(x|\pmb{\theta})-\pmb{0}\right)^T] p(x∣θ)E?[(s(x∣θ)?0)?(s(x∣θ)?0)T] 由于得分函数 s ( x ∣ θ ) s(x|\pmb{\theta}) s(x∣θ) 是尺寸为 m × 1 m\times 1 m×1 的向量,以上协方差是尺寸 m × m m\times m m×m 的协方差矩阵,这就是费舍尔信息矩阵 (Fisher information matrix)的定义,它描述了极大似然估计参数值的置信度(不确定度)的信息,整理如下
F = E p ( x ∣ θ ) [ s ( x ∣ θ ) ? s ( x ∣ θ ) T ] = E p ( x ∣ θ ) [ ▽ θ log ? p ( x ∣ θ ) ? ▽ θ log ? p ( x ∣ θ ) T ] ≈ 1 n ∑ i = 1 n ▽ θ log ? p ( x i ∣ θ ) ? ▽ θ log ? p ( x i ∣ θ ) T \begin{aligned} \mathrm{F} &=\underset{p(x| \pmb{\theta})}{\mathbb{E}}[s(x|\pmb{\theta})·s(x|\pmb{\theta})^T] \\ &= \underset{p(x| \pmb{\theta})}{\mathbb{E}}[ \triangledown _\theta \log p(x|\pmb{\theta}) · \triangledown _\theta \log p(x|\pmb{\theta})^T] \\ & \approx \frac{1}{n}\sum_{i=1}^n \triangledown _\theta \log p(x_i|\pmb{\theta}) · \triangledown _\theta \log p(x_i|\pmb{\theta})^T \end{aligned} F?=p(x∣θ)E?[s(x∣θ)?s(x∣θ)T]=p(x∣θ)E?[▽θ?logp(x∣θ)?▽θ?logp(x∣θ)T]≈n1?i=1∑n?▽θ?logp(xi?∣θ)?▽θ?logp(xi?∣θ)T? -
最后看一下 wiki 百科上关于费舍尔信息矩阵的定义
In information geometry, the Fisher information metric is a particular Riemannian metric which can be defined on a smooth statistical manifold, i.e., a smooth manifold whose points are probability measures defined on a common probability space. lt can be used to calculate the informational difference between measurements. —— wiki
在信息几何学中,费舍尔信息度量是一种特殊的黎曼度量,它可以定义在光滑的统计流形上,这种流形上的点是定义在联合概率空间上的概率密度。费舍尔信息度量可以用来计算测量之间的信息差异
2.2.2 与海森矩阵的关系
-
费舍尔信息矩阵 F \mathrm{F} F 是对数似然函数的海森矩阵 H log ? p ( x ∣ θ ) \mathrm{H}_{\log p(x|\theta)} Hlogp(x∣θ)? 的期望的负值,即
F = ? E p ( x ∣ θ ) [ H log ? p ( x ∣ θ ) ] \mathrm{F} = -\underset{p(x| \pmb{\theta})}{\mathbb{E}}[\mathrm{H}_{\log p(x|\theta)}] F=?p(x∣θ)E?[Hlogp(x∣θ)?] 从直观上看,这意味着费舍尔信息矩阵 F \mathrm{F} F 可以看作对数似然函数 log ? p ( x ∣ θ ) \log p(x|\theta) logp(x∣θ) 的曲率的度量。证明如下首先根据定义,利用求导法则展开对数似然函数的海森矩阵 H log ? p ( x ∣ θ ) H_{\log p(x|\theta)} Hlogp(x∣θ)?
H log ? p ( x ∣ θ ) = ? ? θ ( ? log ? p ( x ∣ θ ) ? θ ) = ? ? θ ( ? p ( x ∣ θ ) p ( x ∣ θ ) ) = H p ( x ∣ θ ) p ( x ∣ θ ) ? ? p ( x ∣ θ ) ? p ( x ∣ θ ) T p ( x ∣ θ ) p ( x ∣ θ ) = H p ( x ∣ θ ) p ( x ∣ θ ) p ( x ∣ θ ) p ( x ∣ θ ) ? ? p ( x ∣ θ ) ? p ( x ∣ θ ) T p ( x ∣ θ ) p ( x ∣ θ ) = H p ( x ∣ θ ) p ( x ∣ θ ) ? ( ? p ( x ∣ θ ) p ( x ∣ θ ) ) ( ? p ( x ∣ θ ) p ( x ∣ θ ) ) T \begin{aligned} \mathrm{H}_{\log p(x \mid \theta)} & =\frac{\partial}{\partial \theta}\left(\frac{\partial \log p(x \mid \theta)}{\partial \theta} \right) \\ & =\frac{\partial}{\partial \theta}\left(\frac{\nabla p(x \mid \theta)}{p(x \mid \theta)}\right) \\ & =\frac{\mathrm{H}_{p(x \mid \theta)} p(x \mid \theta)-\nabla p(x \mid \theta) \nabla p(x \mid \theta)^{\mathrm{T}}}{p(x \mid \theta) p(x \mid \theta)} \\ & =\frac{\mathrm{H}_{p(x \mid \theta)} p(x \mid \theta)}{p(x \mid \theta) p(x \mid \theta)}-\frac{\nabla p(x \mid \theta) \nabla p(x \mid \theta)^{\mathrm{T}}}{p(x \mid \theta) p(x \mid \theta)} \\ & =\frac{\mathrm{H}_{p(x \mid \theta)}}{p(x \mid \theta)}-\left(\frac{\nabla p(x \mid \theta)}{p(x \mid \theta)}\right)\left(\frac{\nabla p(x \mid \theta)}{p(x \mid \theta)}\right)^{\mathrm{T}} \end{aligned} Hlogp(x∣θ)??=?θ??(?θ?logp(x∣θ)?)=?θ??(p(x∣θ)?p(x∣θ)?)=p(x∣θ)p(x∣θ)Hp(x∣θ)?p(x∣θ)??p(x∣θ)?p(x∣θ)T?=p(x∣θ)p(x∣θ)Hp(x∣θ)?p(x∣θ)??p(x∣θ)p(x∣θ)?p(x∣θ)?p(x∣θ)T?=p(x∣θ)Hp(x∣θ)???(p(x∣θ)?p(x∣θ)?)(p(x∣θ)?p(x∣θ)?)T?
进一步取关于 p ( x ∣ θ ) p(x|\theta) p(x∣θ) 的期望,得到
E p ( x ∣ θ ) [ H log ? p ( x ∣ θ ) ] = E p ( x ∣ θ ) [ H p ( x ∣ θ ) p ( x ∣ θ ) ? ( ? p ( x ∣ θ ) p ( x ∣ θ ) ) ( ? p ( x ∣ θ ) p ( x ∣ θ ) ) T ] = E p ( x ∣ θ ) [ H p ( x ∣ θ ) p ( x ∣ θ ) ] ? E p ( x ∣ θ ) [ ( ? p ( x ∣ θ ) p ( x ∣ θ ) ) ( ? p ( x ∣ θ ) p ( x ∣ θ ) ) T ] = ∫ H p ( x ∣ θ ) p ( x ∣ θ ) p ( x ∣ θ ) d x ? E p ( x ∣ θ ) [ ? log ? p ( x ∣ θ ) ? log ? p ( x ∣ θ ) T ] = H ∫ p ( x ∣ θ ) d x ? F = H 1 ? F = ? F . \begin{aligned} \underset{p(x \mid \theta)}{\mathbb{E}}\left[\mathrm{H}_{\log p(x \mid \theta)}\right] & =\underset{p(x \mid \theta)}{\mathbb{E}}\left[\frac{\mathrm{H}_{p(x \mid \theta)}}{p(x \mid \theta)}-\left(\frac{\nabla p(x \mid \theta)}{p(x \mid \theta)}\right)\left(\frac{\nabla p(x \mid \theta)}{p(x \mid \theta)}\right)^{\mathrm{T}}\right] \\ & =\underset{p(x \mid \theta)}{\mathbb{E}}\left[\frac{\mathrm{H}_{p(x \mid \theta)}}{p(x \mid \theta)}\right]-\underset{p(x \mid \theta)}{\mathbb{E}}\left[\left(\frac{\nabla p(x \mid \theta)}{p(x \mid \theta)}\right)\left(\frac{\nabla p(x \mid \theta)}{p(x \mid \theta)}\right)^{\mathrm{T}}\right] \\ & =\int \frac{\mathrm{H}_{p(x \mid \theta)}}{p(x \mid \theta)} p(x \mid \theta) \mathrm{d} x-\underset{p(x \mid \theta)}{\mathbb{E}}\left[\nabla \log p(x \mid \theta) \nabla \log p(x \mid \theta)^{\mathrm{T}}\right] \\ & =\mathrm{H}_{\int p(x \mid \theta) \mathrm{d} x}-\mathrm{F} \\ & =\mathrm{H}_{1}-\mathrm{F} \\ & =-\mathrm{F} . \end{aligned} p(x∣θ)E?[Hlogp(x∣θ)?]?=p(x∣θ)E?[p(x∣θ)Hp(x∣θ)???(p(x∣θ)?p(x∣θ)?)(p(x∣θ)?p(x∣θ)?)T]=p(x∣θ)E?[p(x∣θ)Hp(x∣θ)??]?p(x∣θ)E?[(p(x∣θ)?p(x∣θ)?)(p(x∣θ)?p(x∣θ)?)T]=∫p(x∣θ)Hp(x∣θ)??p(x∣θ)dx?p(x∣θ)E?[?logp(x∣θ)?logp(x∣θ)T]=H∫p(x∣θ)dx??F=H1??F=?F.? -
利用以上关系,在一些优化方法中可以用 F \mathrm{F} F 估计 H \mathrm{H} H,前者往往计算成本较低
2.2.3 与 KL 散度的关系
-
KL 散度是一种常用的度量分布 P , Q P,Q P,Q 间差异的工具,当随机变量是离散或连续值时,计算公式分别为
K L ( P ∥ Q ) = ∑ i = 1 n p ( x ) log ? p ( x ) q ( x ) K L ( P ∥ Q ) = ∫ ? ∞ ∞ p ( x ) log ? ( p ( x ) q ( x ) ) d x \begin{aligned} &\mathrm{KL}(P \| Q)=\sum_{i=1}^{n} p(x) \log \frac{p(x)}{q(x)}\\ &\mathrm{KL}(P \| Q)=\int_{-\infty}^{\infty} p(x) \log \left(\frac{p(x)}{q(x)}\right) d x \end{aligned} ?KL(P∥Q)=i=1∑n?p(x)logq(x)p(x)?KL(P∥Q)=∫?∞∞?p(x)log(q(x)p(x)?)dx? 值得注意的是,KL 散度是非对称的,因此并非一种真实度量,但是当参数变化量趋于零时 KL 散度渐进对称,即
P = p ( x ∣ θ ) Q 1 = p ( x ∣ θ + d ) , Q 2 = p ( x ∣ θ ? d ) K L ( P ∥ Q 1 ) ≈ K L ( P ∥ Q 2 ) , ? d → 0 \begin{aligned} &P=p(x|\pmb{\theta})\\ &Q_1=p(x|\pmb{\theta}+\pmb{d}),\quad Q_2=p(x|\pmb{\theta}-\pmb{d})\\ &\mathrm{KL}(P \| Q_1)\approx \mathrm{KL}(P \| Q_2), \space \pmb{d}\to \pmb{0} \end{aligned} ?P=p(x∣θ)Q1?=p(x∣θ+d),Q2?=p(x∣θ?d)KL(P∥Q1?)≈KL(P∥Q2?),?d→0? 因此也可以将其作为度量使用。关于 KL 散度的详细说明参考 信息论概念详细梳理:信息量、信息熵、条件熵、互信息、交叉熵、KL散度、JS散度 -
费舍尔信息矩阵 F \mathrm{F} F 与 KL 散度之间有重要关系:令 d → 0 \pmb{d}\to\pmb{0} d→0, K L [ p ( x ∣ θ ) ∥ p ( x ∣ θ + d ) ] \mathrm{KL}[p(x|\pmb{\theta}) \| p(x|\pmb{\theta}+\pmb{d})] KL[p(x∣θ)∥p(x∣θ+d)] 的二阶泰勒展开满足
K L [ p ( x ∣ θ ) ∥ p ( x ∣ θ + d ) ] ≈ 1 2 d T F d \mathrm{KL}[p(x|\pmb{\theta}) \| p(x|\pmb{\theta}+\pmb{d})] \approx \frac{1}{2} \pmb{d}^T\pmb{\mathrm{F}}\pmb{d} KL[p(x∣θ)∥p(x∣θ+d)]≈21?dTFd 证明如下首先,给定分布 p ( x ∣ θ ) p(x|\pmb{\theta}) p(x∣θ),考察分布 p ( x ∣ θ ′ ) p(x|\pmb{\theta}') p(x∣θ′) 和它之间的 KL 散度的二阶泰勒展开式子,根据定义有
K L [ p ( x ∣ θ ) ∥ p ( x ∣ θ ′ ) ] = E p ( x ∣ θ ) [ log ? p ( x ∣ θ ) ] ? E p ( x ∣ θ ) [ log ? p ( x ∣ θ ′ ) ] \mathrm{KL}\left[p(x \mid \theta) \| p\left(x \mid \theta^{\prime}\right)\right]=\underset{p(x \mid \theta)}{\mathbb{E}}[\log p(x \mid \theta)]-\underset{p(x \mid \theta)}{\mathbb{E}}\left[\log p\left(x \mid \theta^{\prime}\right)\right] KL[p(x∣θ)∥p(x∣θ′)]=p(x∣θ)E?[logp(x∣θ)]?p(x∣θ)E?[logp(x∣θ′)] 其关于 θ ′ \pmb{\theta}' θ′ 的 一阶梯度为
? θ ′ K L [ p ( x ∣ θ ) ∥ p ( x ∣ θ ′ ) ] = ? θ ′ E p ( x ∣ θ ) [ log ? p ( x ∣ θ ) ] ? ? θ ′ E p ( x ∣ θ ) [ log ? p ( x ∣ θ ′ ) ] = ? E p ( x ∣ θ ) [ ? θ ′ log ? p ( x ∣ θ ′ ) ] \begin{aligned} \nabla_{\theta^{\prime}} \mathrm{KL}\left[p(x \mid \theta) \| p\left(x \mid \theta^{\prime}\right)\right] & =\nabla_{\theta^{\prime}} \underset{p(x \mid \theta)}{\mathbb{E}}[\log p(x \mid \theta)]-\nabla_{\theta^{\prime}} \underset{p(x \mid \theta)}{\mathbb{E}}\left[\log p\left(x \mid \theta^{\prime}\right)\right] \\ & =-\underset{p(x \mid \theta)}{\mathbb{E}}\left[\nabla_{\theta^{\prime}} \log p\left(x \mid \theta^{\prime}\right)\right] \end{aligned} ?θ′?KL[p(x∣θ)∥p(x∣θ′)]?=?θ′?p(x∣θ)E?[logp(x∣θ)]??θ′?p(x∣θ)E?[logp(x∣θ′)]=?p(x∣θ)E?[?θ′?logp(x∣θ′)]? 关于 θ ′ \pmb{\theta}' θ′ 的二阶梯度为
? θ ′ 2 K L [ p ( x ∣ θ ) ∥ p ( x ∣ θ ′ ) ] = ? ∫ p ( x ∣ θ ) ? θ ′ 2 log ? p ( x ∣ θ ′ ) d x = ? ∫ p ( x ∣ θ ) H log ? p ( x ∣ θ ′ ) d x = ? E p ( x ∣ θ ) [ H log ? p ( x ∣ θ ′ ) ] \begin{aligned} \nabla_{\theta^{\prime}}^{2} \mathrm{KL}\left[p(x \mid \theta) \| p\left(x \mid \theta^{\prime}\right)\right] &=-\int p(x \mid \theta) \nabla_{\theta^{\prime}}^{2} \log p\left(x \mid \theta^{\prime}\right) \mathrm{d} x \\ &=-\int p(x \mid \theta) \mathrm{H}_{\log p(x \mid \theta')} \mathrm{d} x \\ &=-\underset{p(x \mid \theta)}{\mathbb{E}}\left[\mathrm{H}_{\log p(x \mid \theta')}\right] \\ \end{aligned} ?θ′2?KL[p(x∣θ)∥p(x∣θ′)]?=?∫p(x∣θ)?θ′2?logp(x∣θ′)dx=?∫p(x∣θ)Hlogp(x∣θ′)?dx=?p(x∣θ)E?[Hlogp(x∣θ′)?]? 得到以上展开式后,进一步考虑在 θ ′ = θ \pmb{\theta}'=\pmb{\theta} θ′=θ 处的展开结果(注意这时把 p ( x ∣ θ ) p(x|\pmb{\theta}) p(x∣θ) 看做不变量),将 p ( x ∣ θ ) p(x|\theta) p(x∣θ) 简记为 p θ p_\theta pθ?,有
? θ ′ K L [ p θ ∥ p θ ′ ] ∣ θ ′ = θ = ? E p ( x ∣ θ ) [ ? θ log ? p ( x ∣ θ ) ] = 0 ( 2.1.1 节得分函数性质) ? θ ′ 2 K L [ p θ ∥ p θ ′ ] ∣ θ ′ = θ = ? E p ( x ∣ θ ) [ H log ? p ( x ∣ θ ) ] = F ( 2.1.2 节 F 和 H 的关系) \begin{aligned} &\left.\nabla_{\theta^{\prime}} \mathrm{KL}\left[p_{\theta} \| p_{\theta^{\prime}}\right]\right|_{\theta^{\prime}=\theta} = -\underset{p(x \mid \theta)}{\mathbb{E}}\left[\nabla_{\theta} \log p\left(x \mid \theta\right)\right] = \pmb{0} && (2.1.1节得分函数性质) \\ &\nabla_{\theta^{\prime}}^{2} \mathrm{KL}\left[p_{\theta} \| p_{\theta^{\prime}}\right]|_{\theta^{\prime}=\theta} = -\underset{p(x \mid \theta)}{\mathbb{E}}\left[\mathrm{H}_{\log p(x \mid \theta)}\right] = \mathrm{F} && (2.1.2节 \mathrm{F} 和 \mathrm{H} 的关系) \end{aligned} ??θ′?KL[pθ?∥pθ′?]∣θ′=θ?=?p(x∣θ)E?[?θ?logp(x∣θ)]=0?θ′2?KL[pθ?∥pθ′?]∣θ′=θ?=?p(x∣θ)E?[Hlogp(x∣θ)?]=F??(2.1.1节得分函数性质)(2.1.2节F和H的关系)?利用以上结果,考察令 d → 0 \pmb{d}\to\pmb{0} d→0 时 K L [ p ( x ∣ θ ) ∥ p ( x ∣ θ + d ) ] \mathrm{KL}[p(x|\pmb{\theta}) \| p(x|\pmb{\theta}+\pmb{d})] KL[p(x∣θ)∥p(x∣θ+d)] 的二阶泰勒展开,将 p ( x ∣ θ ) p(x|\theta) p(x∣θ) 简记为 p θ p_\theta pθ?,有
K L [ p θ ∥ p θ + d ] ≈ K L [ p θ ∥ p θ ] + ( ? θ ′ K L [ p θ ∥ p θ ′ ] ∣ θ ′ = θ ) T d + 1 2 d T ( ? θ ′ 2 K L [ p ( x ∣ θ ) ∥ p ( x ∣ θ ′ ) ] ∣ θ ′ ) d = 0 ? 0 T d + 1 2 d T F d = 1 2 d T F d \begin{aligned} \mathrm{KL}\left[p_{\theta} \| p_{\theta+d}\right] & \approx \mathrm{KL}\left[p_{\theta} \| p_{\theta}\right]+\left(\left.\nabla_{\theta^{\prime}} \mathrm{KL}\left[p_{\theta} \| p_{\theta^{\prime}}\right]\right|_{\theta^{\prime}=\theta}\right)^{\mathrm{T}} d+\frac{1}{2} d^{\mathrm{T}} \left(\nabla_{\theta^{\prime}}^{2} \mathrm{KL}\left[p(x \mid \theta) \| p\left(x \mid \theta^{\prime}\right)\right] |_{\theta^{\prime}} \right) d \\ & = 0 - \pmb{0}^{\mathrm{T}} \pmb{d} + \frac{1}{2} \pmb{d}^{\mathrm{T}} \pmb{\mathrm{F}} \pmb{d} \\ &= \frac{1}{2} \pmb{d}^{\mathrm{T}} \pmb{\mathrm{F}} \pmb{d} \end{aligned} KL[pθ?∥pθ+d?]?≈KL[pθ?∥pθ?]+(?θ′?KL[pθ?∥pθ′?]∣θ′=θ?)Td+21?dT(?θ′2?KL[p(x∣θ)∥p(x∣θ′)]∣θ′?)d=0?0Td+21?dTFd=21?dTFd?
3. 自然梯度法
- 本节对第 0 节中提到的 “欧氏参数空间” 问题做进一步讨论。这里我们主要考虑
最速下降法 (Steepest Descent Method),这类方法基于损失函数/目标函数在当前位置的梯度来确定参数的更新方向(负梯度方向),以使目标函数值下降最快

如上图所示,自然梯度法 (Natural Gradient Descent)的主要特点在于其使用费舍尔信息矩阵这种黎曼度量来调整梯度方向,因此可以考虑到参数空间的流形结构
3.1 使用欧氏空间度量的最速下降法
- 首先,考察优化问题问题中的单步迭代过程,如下对全局优化目标进行分解
min ? θ L ( θ ) ? d k = arg?min ? d L ( θ k + d ) , ?s.t.? ∣ ∣ d ∣ ∣ = 1 \min_{\pmb{\theta}} \mathcal{L}(\pmb{\theta}) \quad \Rightarrow \quad \pmb{d}^k = \argmin_{\pmb{d}} \mathcal{L}(\pmb{\theta}^k+\pmb{d}), \space \text{s.t.} \space ||\pmb{d}||=1 θmin?L(θ)?dk=dargmin?L(θk+d),?s.t.?∣∣d∣∣=1 其中 d \pmb{d} d 是一个方向向量,要求其模长固定为 1。这意味在每一步优化过程中,我们要解一个子优化问题:找出能够使得损失函数 L \mathcal{L} L 减少最快的方向 d \pmb{d} d。接下来在 θ k \pmb{\theta}^k θk 处一阶泰勒展开新的优化目标
L ( θ k + d ) ≈ L ( θ k ) + ▽ θ L ( θ k ) T d \mathcal{L}(\pmb{\theta}^k+\pmb{d}) \approx \mathcal{L}(\pmb{\theta}^k) + \triangledown_{\pmb{\theta}} \mathcal{L}(\pmb{\theta}^k)^T\pmb{d} L(θk+d)≈L(θk)+▽θ?L(θk)Td 其中 L ( θ k ) \mathcal{L}(\pmb{\theta}^k) L(θk) 是一个定值,每步迭代的优化方向为
d k = arg?min ? d ( ▽ θ L ( θ k ) T d ) ?s.t.? ∣ ∣ d ∣ ∣ = 1 \pmb{d}^k = \argmin_{\pmb{d}}\left( \triangledown_{\pmb{\theta}} \mathcal{L}(\pmb{\theta}^k)^T\pmb{d}\right) \space \text{s.t.} \space ||\pmb{d}||=1 dk=dargmin?(▽θ?L(θk)Td)?s.t.?∣∣d∣∣=1 - 当使用不用的范数表达
∣
∣
d
∣
∣
=
1
||\pmb{d}||=1
∣∣d∣∣=1 时,就对应了不同的优化方法
{ ∥ d ∥ 2 = 1 梯度下降法 ∥ d ∥ 1 = 1 坐标下降法? ∥ d ∥ ? 2 L ( d ) = d T ? 2 L ( d ) d = 1 牛顿法? \begin{cases} & \|\pmb{d}\|_{2}=1 && \text {梯度下降法} \\ & \|\pmb{d}\|_{1}=1 && \text {坐标下降法 } \\ & \|\pmb{d}\|_{\nabla^{2} \mathcal{L}(\pmb{d})}=\pmb{d}^{T} \nabla^{2} \mathcal{L}(\pmb{d}) \pmb{d} =1 && \text {牛顿法 } \end{cases} ? ? ???∥d∥2?=1∥d∥1?=1∥d∥?2L(d)?=dT?2L(d)d=1??梯度下降法坐标下降法?牛顿法?? 注意这些都是欧氏空间度量,因此都没有考虑到参数空间的曲率。值得一提的是,牛顿法解出的优化步骤为
θ k + 1 ← θ k ? α H L ? 1 ▽ θ L ( θ k ) \pmb{\theta}^{k+1} \leftarrow \pmb{\theta}^k - \alpha \mathrm{H}_{\mathcal{L}}^{-1} \triangledown_{\pmb{\theta}} \mathcal{L}(\pmb{\theta}^k) θk+1←θk?αHL?1?▽θ?L(θk) 其中 H L \mathrm{H}_{\mathcal{L}} HL? 是损失函数关于参数 θ \pmb{\theta} θ 的二阶导数信息,即海森矩阵
3.2 自然梯度法
- 自然梯度法中,每一步迭代的更新向量(注意这里不要求是单位向量)
d
\pmb{d}
d 如下计算
d k = arg ? min ? d L ( θ k + d ) ??s.t.?? K L [ p θ k ∥ p θ k + d ] = c \pmb{d}^k =\underset{\pmb{d}}{\arg \min } \mathcal{L}(\pmb{\theta}^k+\pmb{d}) \space \text { s.t. } \space\mathrm{KL}\left[p_{\pmb{\theta}^k} \| p_{\pmb{\theta}^k+\pmb{d}}\right]=c dk=dargmin?L(θk+d)??s.t.??KL[pθk?∥pθk+d?]=c 相比 3.1 节的几个方法,该优化目标只是把条件从 ∣ ∣ d ∣ ∣ = 1 ||\pmb{d}||=1 ∣∣d∣∣=1 改成了 K L [ p θ ∥ p θ + d ] = c \mathrm{KL}\left[p_{\pmb{\theta}} \| p_{\pmb{\theta}+\pmb{d}}\right]=c KL[pθ?∥pθ+d?]=c,其中 c c c 是某个常数- 条件 ∣ ∣ d ∣ ∣ = 1 ||\pmb{d}||=1 ∣∣d∣∣=1 约束每一步优化过程中参数变化量 △ θ \triangle \pmb{\theta} △θ 的模长恒定,由于参数空间中存在曲率,这并不能保持 p ( x ∣ θ ) p(x|\pmb{\theta}) p(x∣θ) 分布空间的变化程度恒定
- 条件 K L [ p θ ∥ p θ + d ] = c \mathrm{KL}\left[p_{\pmb{\theta}} \| p_{\pmb{\theta}+\pmb{d}}\right]=c KL[pθ?∥pθ+d?]=c 直接约束模型以恒定的程度在分布空间移动,从而排除了参数空间曲率的影响
- 用拉格朗日乘子法将以最小化转换为无约束优化问题,再在
θ
k
\pmb{\theta}^k
θk 处对
L
(
θ
k
+
d
)
\mathcal{L}(\pmb{\theta}^k+\pmb{d})
L(θk+d) 进行一阶泰勒展开,对
K
L
[
p
θ
k
∥
p
θ
k
+
d
]
\mathrm{KL}\left[p_{\pmb{\theta}^k} \| p_{\pmb{\theta}^k+\pmb{d}}\right]
KL[pθk?∥pθk+d?] 进行二阶泰勒展开(引用2.2.3节
F
\mathrm{F}
F 和 KL 散度的关系)
d k = arg ? min ? d L ( θ k + d ) + λ ( K L [ p θ k ∥ p θ k + d ] ? c ) ≈ arg ? min ? d L ( θ k ) + ? θ L ( θ k ) T d + 1 2 λ d T F d ? λ c . \begin{aligned} \pmb{d}^k & =\underset{\pmb{d}}{\arg \min } \mathcal{L}(\pmb{\theta}^k+\pmb{d})+\lambda\left(\mathrm{KL}\left[p_{\pmb{\theta}^k} \| p_{\pmb{\theta}^k+\pmb{d}}\right]-c\right) \\ & \approx \underset{\pmb{d}}{\arg \min } \mathcal{L}(\pmb{\theta}^k)+\nabla_{\pmb{\theta}} \mathcal{L}(\pmb{\theta}^k)^{\mathrm{T}} \pmb{d}+\frac{1}{2} \lambda \pmb{d}^{\mathrm{T}} \mathrm{F} \pmb{d}-\lambda c . \end{aligned} dk?=dargmin?L(θk+d)+λ(KL[pθk?∥pθk+d?]?c)≈dargmin?L(θk)+?θ?L(θk)Td+21?λdTFd?λc.? 通过令关于 d \pmb{d} d 的偏导数为 0 \pmb{0} 0 来解以上无约束优化问题
0 = ? ? d ( L ( θ k ) + ? θ L ( θ k ) T d + 1 2 λ d T F d ? λ c ) = ? θ L ( θ k ) + λ F d λ F d = ? ? θ L ( θ k ) d = ? 1 λ F ? 1 ? θ L ( θ k ) \begin{aligned} \pmb{0} & =\frac{\partial}{\partial \pmb{d}}\left( \mathcal{L}(\pmb{\theta}^k)+\nabla_{\theta} \mathcal{L}(\pmb{\theta}^k)^{\mathrm{T}} \pmb{d}+\frac{1}{2} \lambda \pmb{d}^{\mathrm{T}} \mathrm{F} \pmb{d}-\lambda c\right) \\ & =\nabla_{\theta} \mathcal{L}(\pmb{\theta}^k)+\lambda \mathrm{F} \pmb{d} \\ \\ \lambda \mathrm{F} \pmb{d} & =-\nabla_{\theta} \mathcal{L}(\pmb{\theta}^k) \\ \pmb{d} & =-\frac{1}{\lambda} \mathrm{F}^{-1} \nabla_{\theta} \mathcal{L}(\pmb{\theta}^k) \end{aligned} 0λFdd?=?d??(L(θk)+?θ?L(θk)Td+21?λdTFd?λc)=?θ?L(θk)+λFd=??θ?L(θk)=?λ1?F?1?θ?L(θk)? 其中 λ \lambda λ 是拉格朗日常数。根据结果可知,使用费舍尔信息矩阵的逆 F ? 1 \mathrm{F}^{-1} F?1,根据参数空间曲率来调节梯度值 ? θ L ( θ k ) \nabla_{\theta} \mathcal{L}(\pmb{\theta}^k) ?θ?L(θk),可以保证每一步优化过程前后模型 p ( x ∣ θ ) p(x|\pmb{\theta}) p(x∣θ) 都以恒定的程度在分布空间移动,实现更稳定的优化过程。 - 下面给出自然梯度法的伪代码

- 自然梯度法的一个问题是:当模型参数量 m m m 比较大时, F m × m \mathrm{F}_{m\times m} Fm×m? 的尺寸会变得非常大,以至于无法计算、存储或求逆。这和牛顿法(要计算海森矩阵)等二阶优化方法在深度学习中不受欢迎其实是相同的问题。解决该问题的一个方法是对 F \mathrm{F} F 或 H \mathrm{H} H 做近似。比如 ADAM 优化方法计算梯度的一阶和二阶矩的移动平均值,其中一阶矩可以看作是动量(和本文关注点无关);二阶矩近似了 F \mathrm{F} F,但将其限制为对角矩阵,这个近似将存储空间从 O ( n 2 ) O(n^2) O(n2) 降低到 O ( n ) O(n) O(n),并且将求逆运算从 O ( n 3 ) O(n^3) O(n3) 降低到 O ( n ) O(n) O(n)。实践证明 ADAM 工作得非常好,已经是目前深度学习中最流行的优化器之一
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!