数据分析为何要学统计学（2）——如何估计总体概率分布

发布时间：2023年12月17日

明确总体的概率分布类型及参数是进行数据分析的基础，这项工作称为分布推断与参数估计。在总体分布及其参数不明确的情况下，我们可以利用手头掌握的样本来完成这项工作。具体过程由以下步骤组成。

第一步，样本统计特性直观估计

我们采用Seaborn软件的histplot函数绘制核密度分布图（一种通过核密度函数KDE估计得出的近似概率密度曲线与频数分布直方图的合体）。参考代码如下：

import numpy as np
#输入样本数据
x=np.array([2.12906357, 0.72736725, 1.05152821, 0.48600398, 1.91963227,
        1.62165678, 8.86319952, 0.24399412, 4.19883103, 2.80846683,
        1.34644303, 0.35146917, 1.7575424 , 3.90572887, 1.07404978,
        4.05247124, 0.65839571, 0.40166037, 2.03241598, 0.53592929])
import seaborn as sns
#绘制核密度分布图。kde=True会绘制概率密度曲线，否则只有直方图
sns.histplot(x,kde=True)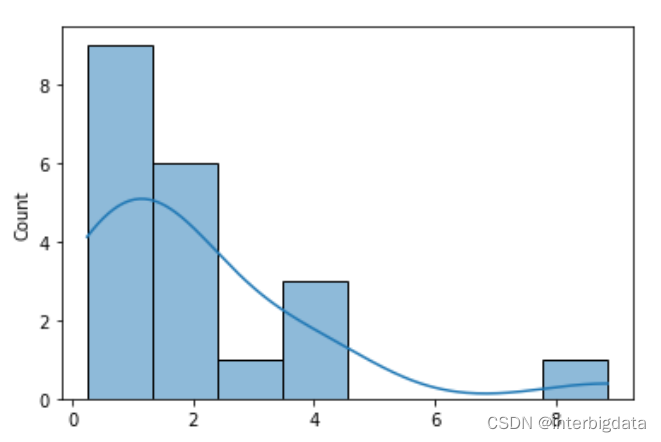

说明：由于KDE是对称函数，所以估计出的概率密度曲线是一条
凸曲线（最高点两侧都有曲线）。即使实际概率密度曲线为??单调
曲线（如指数分布），其近似函数的曲线也是凸的，只不过??????一侧
曲线很长，而另一侧很短。

第二步，确定几个与之相近的候选概率分布（一般3个左右）。

从上图来看，可以根据概率密度曲线选择最相似的卡方分布、指数分布、伽玛分布。

第三步，分别拟合候选分布的参数，并使用拟合得出的分布参数检验每一个候选分布。

代码如下:

import scipy.stats as stats
#构造候选分布集合
dists={'expon':stats.expon,'chi2':stats.chi2,'gamma':stats.gamma}

for dist in dists:
    #拟合每一个分布,将参数存放于param。不同分布参数会不同，但最后两个分别为loc和scale
    #loc和scale代表的含义因分布不同而异，如正态分布norm的情况,loc是均值scale是标准差
    #具体可查看分布类的__doc__属性值中的相关介绍
    param=dists[dist].fit(x)
    
    #检验每一个分布。KS检测是分布推断的常用方法，第一个参数是样本，第二个参数是分布的累计分布函数，第三个是分布参数
    test=stats.kstest(x,dists[dist].cdf,params)
    
    print(dist,test.pvalue,params)

第四步，选择p值（输出结果中的第一列值）最大的作为最终的分布（括号内是分布参数）

expon 0.9001 (0.016, 1.91)
chi2  0.3800 (1.78, 0.016, 1.37)
gamma 0.8080 (0.94, 0.016, 1.95)

?从以上数据可以看出，样本最可能是参数 $\frac{1}{ \lambda }=1.91$ 的指数分布。而事实上，原始样本确实是以 $\frac{1}{ \lambda }=2$ 生成的随机数样本。因为用样本拟合总体总存在一定水平的误差，所以不能追求结果的完美性。

最后我们专门介绍正态分布检验及其参数估计。

正太分布有多种检验方法，分别针对不同的情况

Shapiro–Wilk test：适用于小样本（3-5000），检验函数为scipy的stats.shapiro，根据p值是否大于显著水平a进行判断。公认小样本效果最可靠。

Anderson–Darling test:适用于极小样本（8-26），检验函数为scipy的stats.anderson。可以检'norm, expon, logistic, gumbel,'gumbel_l, gumbel_r, extreme1, weibull_min分布，默认正态分布（norm）。该方法不输出p值，因此需要根据统计量是否小于显著水平对于的阈值来判断。

AndersonResult(statistic=0.8978770382274689, 
critical_values=array([0.527, 0.6  , 0.719, 0.839, 0.998 ]), significance_level=array([15. , 10. ,  5. ,  2.5,  1. ]), 
fit_result=  params: FitParams(loc=1.9203141072704806, scale=0.2784872286328154,
success: True,
message: '`anderson` successfully fit the distribution to the data.')

在该结果中，统计量小于1%显著水平的阈值，所以在该水平下才可以接受服从正态分布，其他显著水平下都拒绝接受服从正态分布的假设。

D'Agostino's K-squared test （Skewness-Kurtosis test）:适用于8个以上的样本，样本容量越大越有效。公认大样本最有效。检验函数为scipy的stats.normaltest，根据p值是否大于显著水平a进行判断。

当样本通过正太分布检验后，可以使用stats.norm.fit函数获得分布参数。