代码随想录算法训练营 | day60 单调栈 84.柱状图中最大的矩形

刷题

84.柱状图中最大的矩形

题目链接 | 文章讲解 | 视频讲解

题目：给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

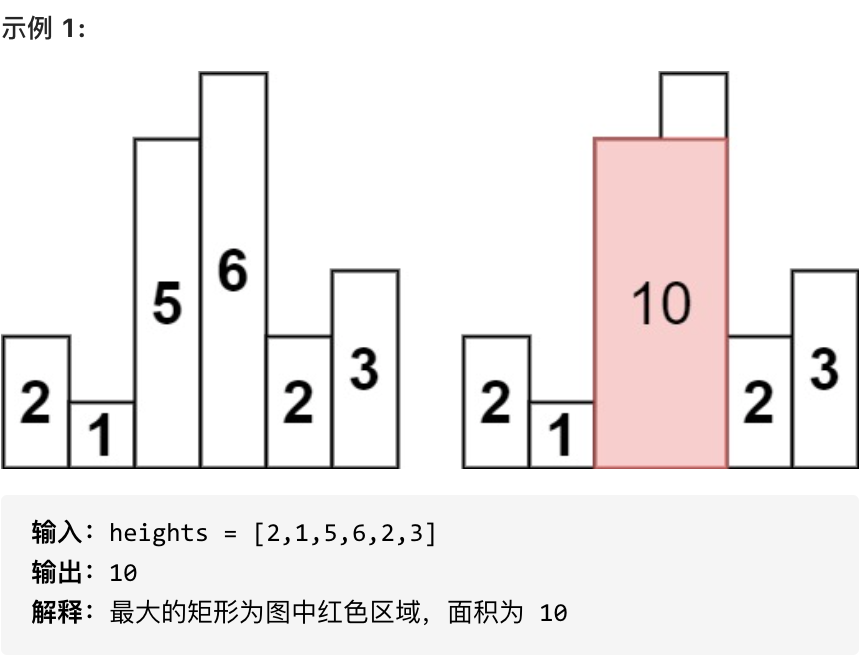
• 1 <= heights.length <=10^5

• 0 <= heights[i] <= 10^4

思路及实现

42. 接雨水?是找每个柱子左右两边第一个大于该柱子高度的柱子，而本题是找每个柱子左右两边第一个小于该柱子的柱子。

这里就涉及到了单调栈很重要的性质，就是单调栈里的顺序，是从小到大还是从大到小。

在题解42. 接雨水中我讲解了接雨水的单调栈从栈头（元素从栈头弹出）到栈底的顺序应该是从小到大的顺序。

那么因为本题是要找每个柱子左右两边第一个小于该柱子的柱子，所以从栈头（元素从栈头弹出）到栈底的顺序应该是从大到小的顺序！

我来举一个例子，如图：

只有栈里从大到小的顺序，才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子。

所以本题单调栈的顺序正好与接雨水反过来。

此时大家应该可以发现其实就是栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度

理解这一点，对单调栈就掌握的比较到位了。

除了栈内元素顺序和接雨水不同，剩下的逻辑就都差不多了，在题解42. 接雨水?我已经对单调栈的各个方面做了详细讲解，这里就不赘述了。

主要就是分析清楚如下三种情况：

• 情况一：当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况

• 情况二：当前遍历的元素heights[i]等于栈顶元素heights[st.top()]的情况

• 情况三：当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况

代码如下：

class Solution {
    int largestRectangleArea(int[] heights) {
        Stack<Integer> st = new Stack<Integer>();
        
        // 数组扩容，在头和尾各加入一个元素
        int [] newHeights = new int[heights.length + 2];
        newHeights[0] = 0;
        newHeights[newHeights.length - 1] = 0;
        for (int index = 0; index < heights.length; index++){
            newHeights[index + 1] = heights[index];
        }

        heights = newHeights;
        
        st.push(0);
        int result = 0;
        // 第一个元素已经入栈，从下标1开始
        for (int i = 1; i < heights.length; i++) {
            // 注意heights[i] 是和heights[st.top()] 比较 ，st.top()是下标
            if (heights[i] > heights[st.peek()]) {
                st.push(i);
            } else if (heights[i] == heights[st.peek()]) {
                st.pop(); // 这个可以加，可以不加，效果一样，思路不同
                st.push(i);
            } else {
                while (heights[i] < heights[st.peek()]) { // 注意是while
                    int mid = st.peek();
                    st.pop();
                    int left = st.peek();
                    int right = i;
                    int w = right - left - 1;
                    int h = heights[mid];
                    result = Math.max(result, w * h);
                }
                st.push(i);
            }
        }
        return result;
    }
}