初中数学：几何题的相关解题原则总结

一、多问类型的几何题

我们做题，应该都遇到过这类几何题目，就是，三个小问，每个小问对应一个几何图像，而且，渐渐复杂。这种题目，大多数有一个变化的条件，比如，动点、角度变化、线段长度变化。
例如下面这个题目：

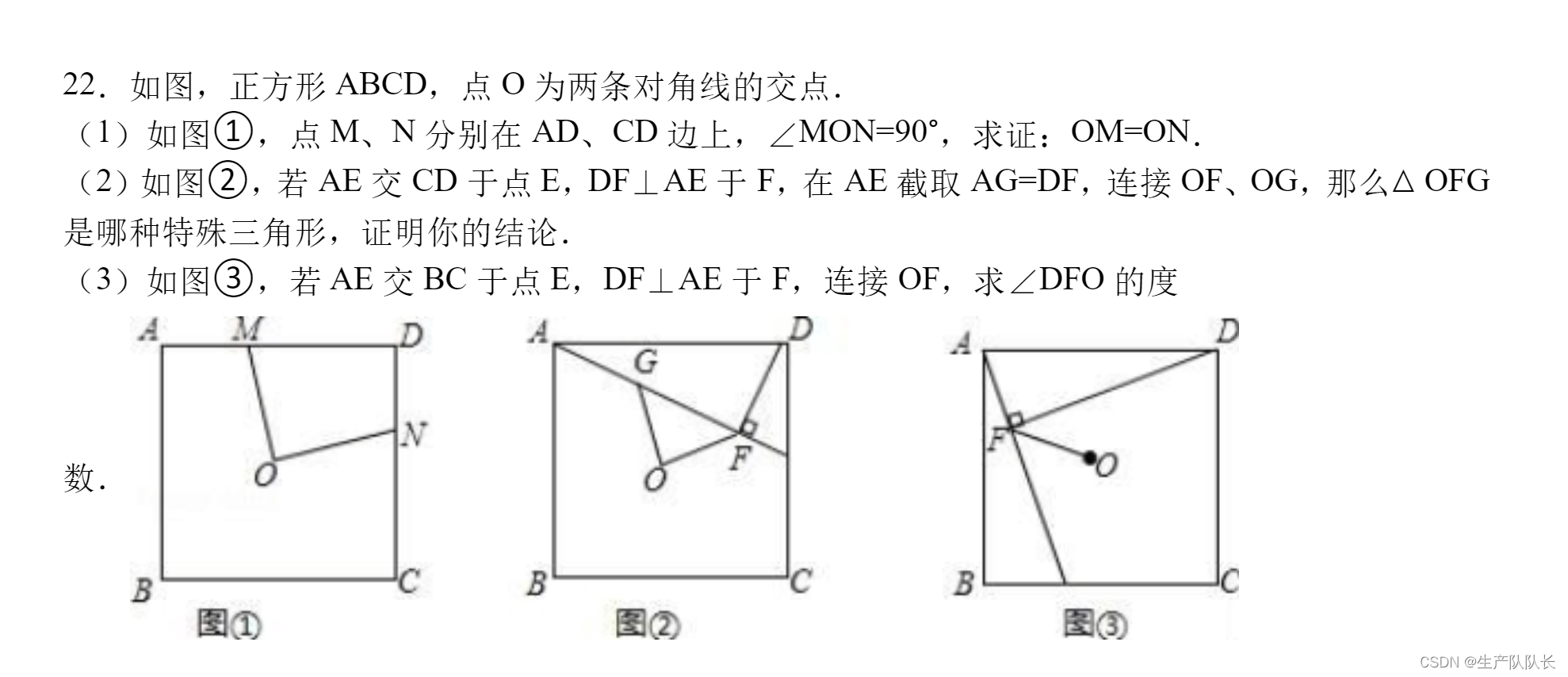
这种题目的做题思路，就是，一定要把题目联系起来，前面题目的结论一定会在后面的题目中起作用。所以，当一时间想不到思路时，一定要联系前面的题目，找思路。

二、辅助线的添加

一般我们能解决1条或者2条辅助线添加的题目。
如果是2条以上的辅助线添加，那就很难想到了。

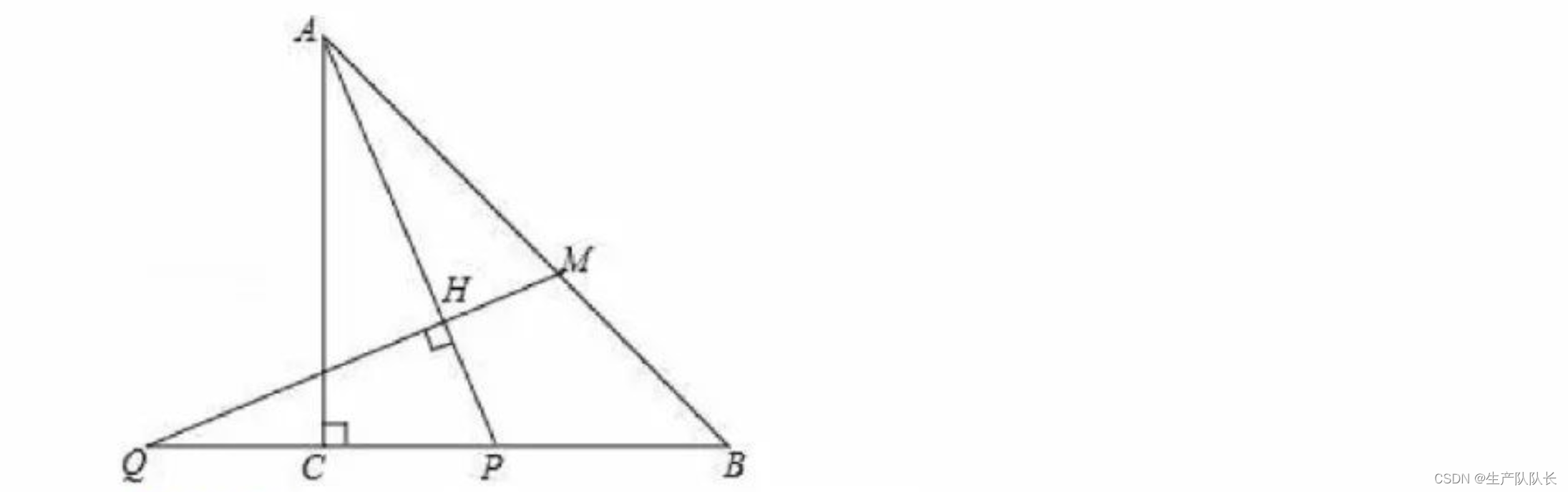
第二小问的辅助线添加如下图：

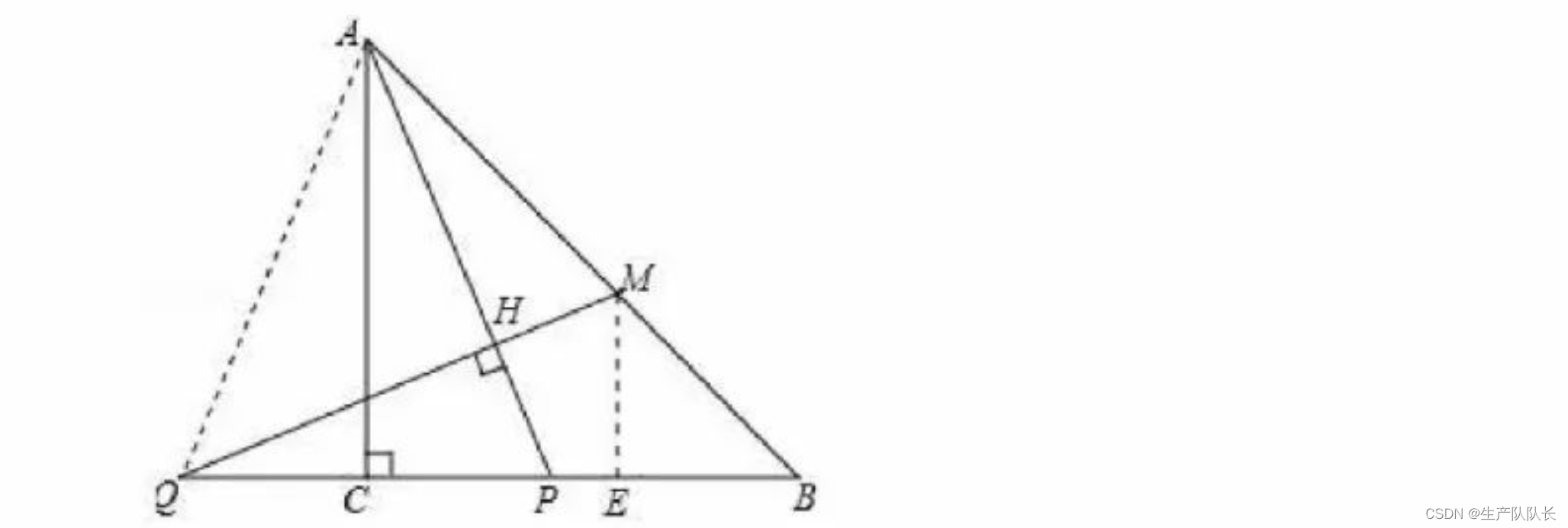
这里，用这道题引出辅助线的添加思路
在三角形中，我们学习过全等，相似，直角三角形等，以及这些三角形所具有的相关性质定理。
于是，我们在添加辅助线时，要么构建全等三角形，要么构建相似三角形，或者特殊三角形等。
所以，我们看已知条件给了什么，相应的去添加辅助线即可。

比如此题
AQ辅助线的添加，我们发现线段QC=PC，AC=AC，∠ACQ=∠ACP。所以，添加AQ，构建了一组全等三角形。
在根据第一小问，发现，∠QAM=∠AMA，所以，AQ=MQ。
此时，就会想到添加ME线段，构建一组全等三角形
从而解决题目。

当然，以上两个学习经验，需要进行大量的练习去体会，提升自己的思维能力，以及对定理，性质的运用熟练度。