曲线生成 | 基于多项式插值的轨迹规划(附ROS C++/Python/Matlab仿真)
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 多项式插值
多项式插值(polynomial interpolation)基于一元多项式进行曲线插值,可以保证微分约束的连续性,使轨迹平滑、机械冲击小。多项式插值的应用场景非常广泛,例如
- 信号处理:在数字信号处理中,多项式插值可以用于重建缺失的信号数据,如图像或音频;
- 数据拟合:在数据分析中,多项式插值可以用于拟合数据,从而探究变量之间的关系;
- 数值微积分:在求解微积分问题时,多项式插值可以用于计算积分或导数,因为它可以在给定区间内精确地近似函数;
- 工程设计:多项式插值可以用于工程设计中的机器人轨迹规划、飞行器控制等领域,因为它可以通过已知的起点和终点来生成平滑的路径
必须指出,当使用等距多项式插值时,随着多项式阶数升高,可能造成函数解析区间过小,产生龙格现象(runge phenomenon):插值两端产生剧烈振荡。因此多项式插值一般采用三次、五次或七次。

2 多项式插值轨迹规划
对路径进行多项式插值时,需要给定机器人在首末位置的位姿以及速度、加速度等微分项作为约束条件。若要求在时间 t 0 t_0 t0?内经过两个路径点 θ ( 0 ) \boldsymbol{\theta }\left( 0 \right) θ(0)、 θ ( t 0 ) \boldsymbol{\theta }\left( t_0 \right) θ(t0?),再考虑首末点的速度约束 θ ˙ ( 0 ) \boldsymbol{\dot{\theta}}\left( 0 \right) θ˙(0)、 θ ˙ ( t 0 ) \boldsymbol{\dot{\theta}}\left( t_0 \right) θ˙(t0?)共四个自由度,由三次多项式可完全确定
θ ( t ) = a 0 + a 1 t + a 2 t 2 + a 3 t 3 \boldsymbol{\theta }\left( t \right) =\boldsymbol{a}_0+\boldsymbol{a}_1t+\boldsymbol{a}_2t^2+\boldsymbol{a}_3t^3 θ(t)=a0?+a1?t+a2?t2+a3?t3
其中多项式系数由位置约束和速度约束确定
[ θ ( 0 ) θ ( t 0 ) θ ˙ ( 0 ) θ ˙ ( t 0 ) ] = [ 1 0 0 0 1 t 0 t 0 2 t 0 3 0 1 0 0 0 1 2 t 0 3 t 0 2 ] [ a 0 a 1 a 2 a 3 ] ? [ a 0 a 1 a 2 a 3 ] = [ θ ( 0 ) θ ˙ ( 0 ) 3 t 0 2 [ θ ( t 0 ) ? θ ( 0 ) ] ? 2 t 0 θ ˙ ( 0 ) ? 1 t 0 θ ˙ ( t 0 ) ? 2 t 0 3 [ θ ( t 0 ) ? θ ( 0 ) ] + 1 t 0 2 [ θ ˙ ( 0 ) ? θ ˙ ( t 0 ) ] ] \left[ \begin{array}{c} \boldsymbol{\theta }\left( 0 \right)\\ \boldsymbol{\theta }\left( t_0 \right)\\ \boldsymbol{\dot{\theta}}\left( 0 \right)\\ \boldsymbol{\dot{\theta}}\left( t_0 \right)\\\end{array} \right] =\left[ \begin{matrix} 1& 0& 0& 0\\ 1& t_0& t_{0}^{2}& t_{0}^{3}\\ 0& 1& 0& 0\\ 0& 1& 2t_0& 3t_{0}^{2}\\\end{matrix} \right] \left[ \begin{array}{c} \boldsymbol{a}_0\\ \boldsymbol{a}_1\\ \boldsymbol{a}_2\\ \boldsymbol{a}_3\\\end{array} \right] \\ \Leftrightarrow \left[ \begin{array}{c} \boldsymbol{a}_0\\ \boldsymbol{a}_1\\ \boldsymbol{a}_2\\ \boldsymbol{a}_3\\\end{array} \right] =\left[ \begin{array}{c} \boldsymbol{\theta }\left( 0 \right)\\ \boldsymbol{\dot{\theta}}\left( 0 \right)\\ \frac{3}{t_{0}^{2}}\left[ \boldsymbol{\theta }\left( t_0 \right) -\boldsymbol{\theta }\left( 0 \right) \right] -\frac{2}{t_0}\boldsymbol{\dot{\theta}}\left( 0 \right) -\frac{1}{t_0}\boldsymbol{\dot{\theta}}\left( t_0 \right)\\ -\frac{2}{t_{0}^{3}}\left[ \boldsymbol{\theta }\left( t_0 \right) -\boldsymbol{\theta }\left( 0 \right) \right] +\frac{1}{t_{0}^{2}}\left[ \boldsymbol{\dot{\theta}}\left( 0 \right) -\boldsymbol{\dot{\theta}}\left( t_0 \right) \right]\\\end{array} \right] ?θ(0)θ(t0?)θ˙(0)θ˙(t0?)? ?= ?1100?0t0?11?0t02?02t0??0t03?03t02?? ? ?a0?a1?a2?a3?? ?? ?a0?a1?a2?a3?? ?= ?θ(0)θ˙(0)t02?3?[θ(t0?)?θ(0)]?t0?2?θ˙(0)?t0?1?θ˙(t0?)?t03?2?[θ(t0?)?θ(0)]+t02?1?[θ˙(0)?θ˙(t0?)]? ?
再考虑首末点的加速度约束 θ ¨ ( 0 ) \boldsymbol{\ddot{\theta}}\left( 0 \right) θ¨(0)、 θ ¨ ( t 0 ) \boldsymbol{\ddot{\theta}}\left( t_0 \right) θ¨(t0?)共六个自由度,由五次多项式曲线可完全确定
θ ( t ) = a 0 + a 1 t + a 2 t 2 + a 3 t 3 + a 4 t 4 + a 5 t 5 \boldsymbol{\theta }\left( t \right) =\boldsymbol{a}_0+\boldsymbol{a}_1t+\boldsymbol{a}_2t^2+\boldsymbol{a}_3t^3+\boldsymbol{a}_4t^4+\boldsymbol{a}_5t^5 θ(t)=a0?+a1?t+a2?t2+a3?t3+a4?t4+a5?t5
其中多项式系数由位置约束、速度约束和加速度约束确定
[ θ ( 0 ) θ ( t 0 ) θ ˙ ( 0 ) θ ˙ ( t 0 ) θ ¨ ( 0 ) θ ¨ ( t 0 ) ] = [ l 1 0 0 0 0 0 1 t 0 t 0 2 t 0 3 t 0 4 t 0 5 0 1 0 0 0 0 0 1 2 t 0 3 t 0 2 4 t 0 3 5 t 0 4 0 0 2 0 0 0 0 0 2 6 t 0 12 t 0 2 20 t 0 3 ] [ a 0 a 1 a 2 a 3 a 4 a 5 ] ? [ a 0 a 1 a 2 a 3 a 4 a 5 ] = [ θ ( 0 ) θ ˙ ( 0 ) 1 2 θ ¨ ( 0 ) 10 t 0 3 [ θ ( t 0 ) ? θ ( 0 ) ] ? 1 t 0 2 [ 4 θ ˙ ( t 0 ) + 6 θ ˙ ( 0 ) ] + 1 2 t 0 [ θ ¨ ( t 0 ) ? 3 θ ¨ ( 0 ) ] ? 15 t 0 4 [ θ ( t 0 ) ? θ ( 0 ) ] + 1 t 0 3 [ 7 θ ˙ ( t 0 ) + 8 θ ˙ ( 0 ) ] ? 1 2 t 0 2 [ 2 θ ¨ ( t 0 ) ? 3 θ ¨ ( 0 ) ] 6 t 0 5 [ θ ( t 0 ) ? θ ( 0 ) ] ? 1 t 0 4 [ 3 θ ˙ ( t 0 ) + 3 θ ˙ ( 0 ) ] + 1 2 t 0 3 [ θ ¨ ( t 0 ) ? θ ¨ ( 0 ) ] ] \left[ \begin{array}{c} \boldsymbol{\theta }\left( 0 \right)\\ \boldsymbol{\theta }\left( t_0 \right)\\ \boldsymbol{\dot{\theta}}\left( 0 \right)\\ \boldsymbol{\dot{\theta}}\left( t_0 \right)\\ \boldsymbol{\ddot{\theta}}\left( 0 \right)\\ \boldsymbol{\ddot{\theta}}\left( t_0 \right)\\\end{array} \right] =\left[ \begin{matrix}{l} 1& 0& 0& 0& 0& 0\\ 1& t_0& t_{0}^{2}& t_{0}^{3}& t_{0}^{4}& t_{0}^{5}\\ 0& 1& 0& 0& 0& 0\\ 0& 1& 2t_0& 3t_{0}^{2}& 4t_{0}^{3}& 5t_{0}^{4}\\ 0& 0& 2& 0& 0& 0\\ 0& 0& 2& 6t_0& 12t_{0}^{2}& 20t_{0}^{3}\\\end{matrix} \right] \left[ \begin{array}{c} \boldsymbol{a}_0\\ \boldsymbol{a}_1\\ \boldsymbol{a}_2\\ \boldsymbol{a}_3\\ \boldsymbol{a}_4\\ \boldsymbol{a}_5\\\end{array} \right]\\ \Leftrightarrow \left[ \begin{array}{c} \boldsymbol{a}_0\\ \boldsymbol{a}_1\\ \boldsymbol{a}_2\\ \boldsymbol{a}_3\\ \boldsymbol{a}_4\\ \boldsymbol{a}_5\\\end{array} \right] =\left[ \begin{array}{c} \boldsymbol{\theta }\left( 0 \right)\\ \boldsymbol{\dot{\theta}}\left( 0 \right)\\ \frac{1}{2}\boldsymbol{\ddot{\theta}}\left( 0 \right)\\ \frac{10}{t_{0}^{3}}\left[ \boldsymbol{\theta }\left( t_0 \right) -\boldsymbol{\theta }\left( 0 \right) \right] -\frac{1}{t_{0}^{2}}\left[ 4\boldsymbol{\dot{\theta}}\left( t_0 \right) +6\boldsymbol{\dot{\theta}}\left( 0 \right) \right] +\frac{1}{2t_0}\left[ \boldsymbol{\ddot{\theta}}\left( t_0 \right) -3\boldsymbol{\ddot{\theta}}\left( 0 \right) \right]\\ \frac{-15}{t_{0}^{4}}\left[ \boldsymbol{\theta }\left( t_0 \right) -\boldsymbol{\theta }\left( 0 \right) \right] +\frac{1}{t_{0}^{3}}\left[ 7\boldsymbol{\dot{\theta}}\left( t_0 \right) +8\boldsymbol{\dot{\theta}}\left( 0 \right) \right] -\frac{1}{2t_{0}^{2}}\left[ 2\boldsymbol{\ddot{\theta}}\left( t_0 \right) -3\boldsymbol{\ddot{\theta}}\left( 0 \right) \right]\\ \frac{6}{t_{0}^{5}}\left[ \boldsymbol{\theta }\left( t_0 \right) -\boldsymbol{\theta }\left( 0 \right) \right] -\frac{1}{t_{0}^{4}}\left[ 3\boldsymbol{\dot{\theta}}\left( t_0 \right) +3\boldsymbol{\dot{\theta}}\left( 0 \right) \right] +\frac{1}{2t_{0}^{3}}\left[ \boldsymbol{\ddot{\theta}}\left( t_0 \right) -\boldsymbol{\ddot{\theta}}\left( 0 \right) \right]\\\end{array} \right] ?θ(0)θ(t0?)θ˙(0)θ˙(t0?)θ¨(0)θ¨(t0?)? ?= ?l110000?0t0?1100?0t02?02t0?22?0t03?03t02?06t0??0t04?04t03?012t02??0t05?05t04?020t03?? ? ?a0?a1?a2?a3?a4?a5?? ?? ?a0?a1?a2?a3?a4?a5?? ?= ?θ(0)θ˙(0)21?θ¨(0)t03?10?[θ(t0?)?θ(0)]?t02?1?[4θ˙(t0?)+6θ˙(0)]+2t0?1?[θ¨(t0?)?3θ¨(0)]t04??15?[θ(t0?)?θ(0)]+t03?1?[7θ˙(t0?)+8θ˙(0)]?2t02?1?[2θ¨(t0?)?3θ¨(0)]t05?6?[θ(t0?)?θ(0)]?t04?1?[3θ˙(t0?)+3θ˙(0)]+2t03?1?[θ¨(t0?)?θ¨(0)]? ?
若考虑更多时间微分约束,则需要更高次数的多项式曲线,但多项式阶数的升高会影响计算效率,从而降低实时性。
3 算法仿真
3.1 ROS C++仿真
核心代码如下所示
Poly::Poly(std::tuple<double, double, double> state_0, std::tuple<double, double, double> state_1, double t)
{
double x0, v0, a0;
double xt, vt, at;
std::tie(x0, v0, a0) = state_0;
std::tie(xt, vt, at) = state_1;
Eigen::Matrix3d A;
A << std::pow(t, 3), std::pow(t, 4), std::pow(t, 5), 3 * std::pow(t, 2), 4 * std::pow(t, 3), 5 * std::pow(t, 4),
6 * t, 12 * std::pow(t, 2), 20 * std::pow(t, 3);
Eigen::Vector3d b(xt - x0 - v0 * t - a0 * t * t / 2, vt - v0 - a0 * t, at - a0);
Eigen::Vector3d x = A.lu().solve(b);
// Quintic polynomial coefficient
p0 = x0;
p1 = v0;
p2 = a0 / 2.0;
p3 = x(0);
p4 = x(1);
p5 = x(2);
}
这部分实现的是五次多项式的系数计算
在轨迹规划过程中,只需要遍历路径点,在相邻路径点间进行插值即可
bool Polynomial::run(const Poses2d points, Points2d& path)
{
if (points.size() < 4)
return false;
else
{
path.clear();
// generate velocity and acceleration constraints heuristically
std::vector<double> v(points.size(), 1.0);
v[0] = 0.0;
std::vector<double> a;
for (size_t i = 0; i < points.size() - 1; i++)
a.push_back((v[i + 1] - v[i]) / 5);
a.push_back(0.0);
for (size_t i = 0; i < points.size() - 1; i++)
{
PolyTrajectory traj;
PolyState start(std::get<0>(points[i]), std::get<1>(points[i]), std::get<2>(points[i]), v[i], a[i]);
PolyState goal(std::get<0>(points[i + 1]), std::get<1>(points[i + 1]), std::get<2>(points[i + 1]), v[i + 1],
a[i + 1]);
generation(start, goal, traj);
Points2d path_i = traj.toPath();
path.insert(path.end(), path_i.begin(), path_i.end());
}
return !path.empty();
}
}
3.2 Python仿真
核心代码如下所示
class Poly:
'''
Polynomial interpolation solver
'''
def __init__(self, state0: tuple, state1: tuple, t: float) -> None:
x0, v0, a0 = state0
xt, vt, at = state1
A = np.array([[t ** 3, t ** 4, t ** 5],
[3 * t ** 2, 4 * t ** 3, 5 * t ** 4],
[6 * t, 12 * t ** 2, 20 * t ** 3]])
b = np.array([xt - x0 - v0 * t - a0 * t ** 2 / 2,
vt - v0 - a0 * t,
at - a0])
X = np.linalg.solve(A, b)
# Quintic polynomial coefficient
self.p0 = x0
self.p1 = v0
self.p2 = a0 / 2.0
self.p3 = X[0]
self.p4 = X[1]
self.p5 = X[2]

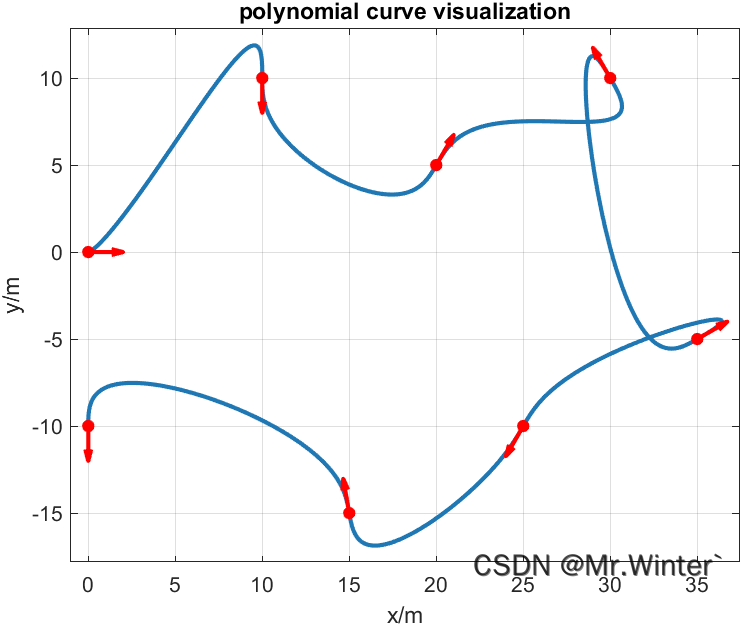
3.3 Matlab仿真
核心代码如下所示
for T = param.t_min : param.step : param.t_max
A = [power(T, 3), power(T, 4), power(T, 5);
3 * power(T, 2), 4 * power(T, 3), 5 * power(T, 4);
6 * T, 12 * power(T, 2), 20 * power(T, 3)];
b = [gx - sx - sv_x * T - sa_x * T * T / 2;
gv_x - sv_x - sa_x * T;
ga_x - sa_x];
X = A \ b;
px = [sx, sv_x, sa_x / 2, X(1), X(2), X(3)];
b = [gy - sy - sv_y * T - sa_y * T * T / 2;
gv_y - sv_y - sa_y * T;
ga_y - sa_y];
X = A \ b;
py = [sy, sv_y, sa_y / 2, X(1), X(2), X(3)];
for t=0 : param.dt : T + param.dt
traj_x = [traj_x, x(px, t)];
traj_y = [traj_y, x(py, t)];
vx = dx(px, t); vy = dx(py, t);
traj_v = [traj_v, hypot(vx, vy)];
ax = ddx(px, t); ay = ddx(py, t);
a = hypot(ax, ay);
if (length(traj_v) >= 2) && (traj_v(end) < traj_v(end - 1))
a = -a;
end
traj_a = [traj_a, a];
jx = dddx(px, t); jy = dddx(py, t);
j = hypot(jx, jy);
if (length(traj_a) >= 2) && (traj_a(end) < traj_a(end - 1))
j = -j;
end
traj_j = [traj_j, j];
end
if ((max(abs(traj_a)) < param.max_acc) && (max(abs(traj_j)) < param.max_jerk))
break;
else
traj_x = []; traj_y = [];
traj_v = []; traj_a = []; traj_j = [];
end
end
完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 将csdn博客转成md格式文档
- 【设计模式】之工厂模式
- php think run 和springBoot的main启动的顺序,有什么相同与不同的地方
- macbookpro怎么录屏?Camtasia Studio2023进行屏幕录制的方法教程
- 平价运动蓝牙耳机什么牌子好、好用的平价运动耳机
- 【年终总结】回首2023的精彩,迈向2024的未来
- 标准库--默认分配器
- 搭建《幻兽帕鲁》服务器需要怎样配置的云服务器?
- k8s集群内部署nacos集群
- yolov5_obb win10环境安装