Note8---归并排序+计数排序

---

目录

前言👻

1. 归并基本思想💋

2. 归并---递归版🧚🏻?♀?

2.1 思路分析🪢

2.2 代码实现🧵

2.2.1 sort.h

2.2.2 sort.c

2.2.3 test.c

2.3 性能对比🧶

3. 归并---非递归版🧤

3.1 思路分析🎩

3.2 代码实现🧢

3.2.1 sort.h

3.2.2 sort.c

3.2.3 test.c

4.?归并排序的特性总结

5. 非比较排序---计数排序👔

5.1 基本思想👑

5.2 思路分析🐹

5.3?代码实现🐸

5.3.1 sort.h

5.3.2 sort.c

5.3.3 test.c

5.4 性能对比

6. 计数排序特性总结🐯

7.?排序算法复杂度及稳定性分析🐲

后语🤡

---

前言👻

又见面了，小伙伴们！!最近忙碌的期末周总算是结束了！上篇博客，我们一起学习了交换排序：冒泡排序和快速排序的相关知识点。今天我来将上次剩下的归并排序和计数排序补给大家！下面，开始今天的学习吧！

---

1. 归并基本思想💋

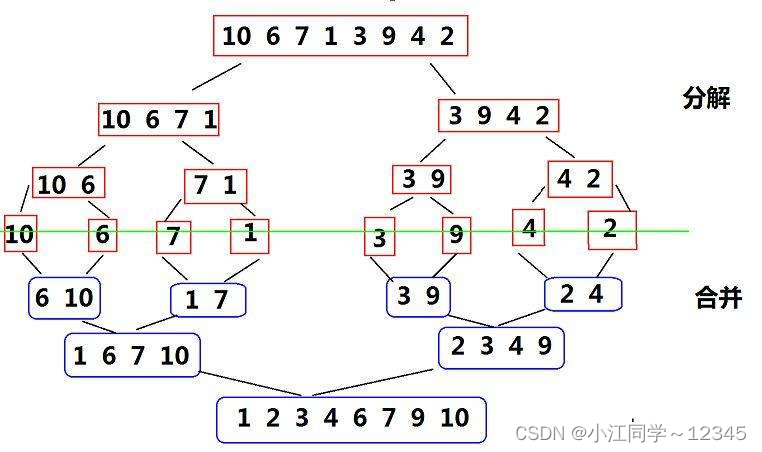
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：

---

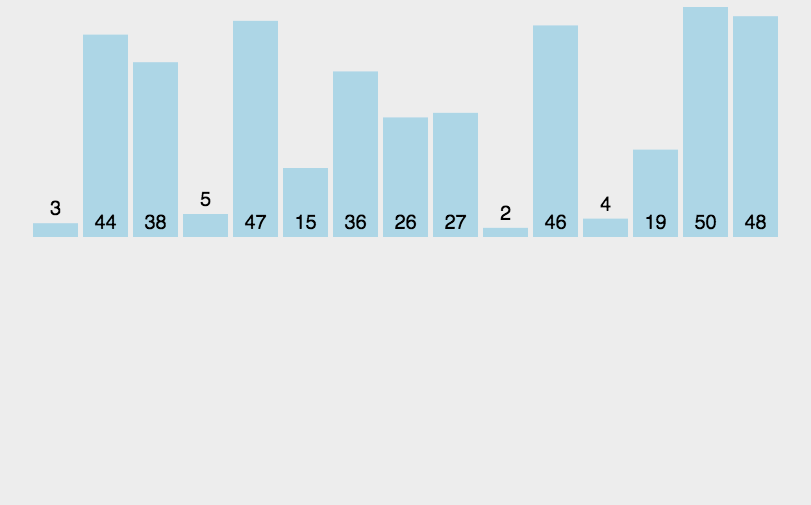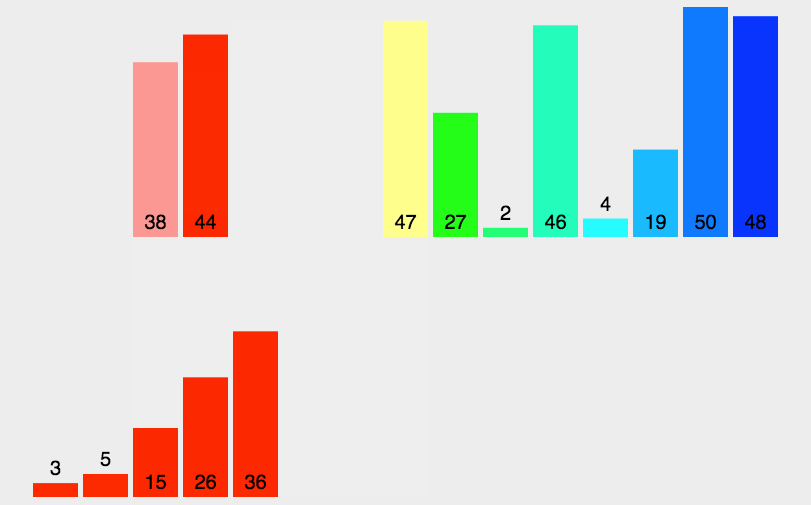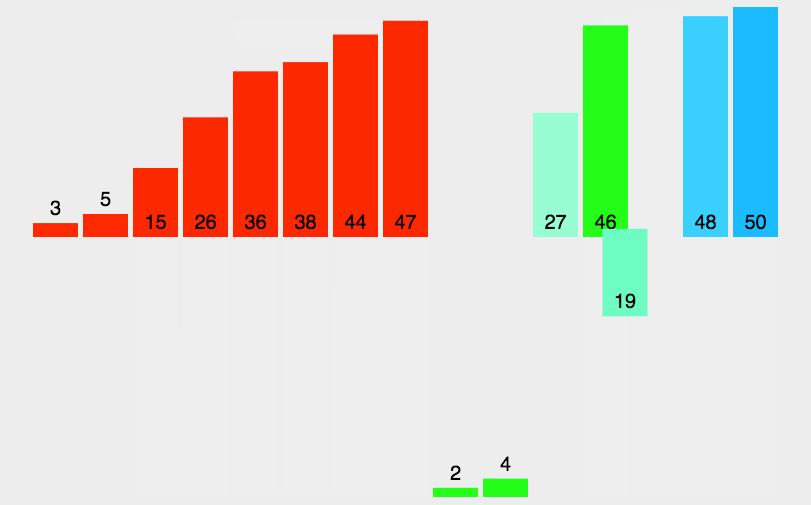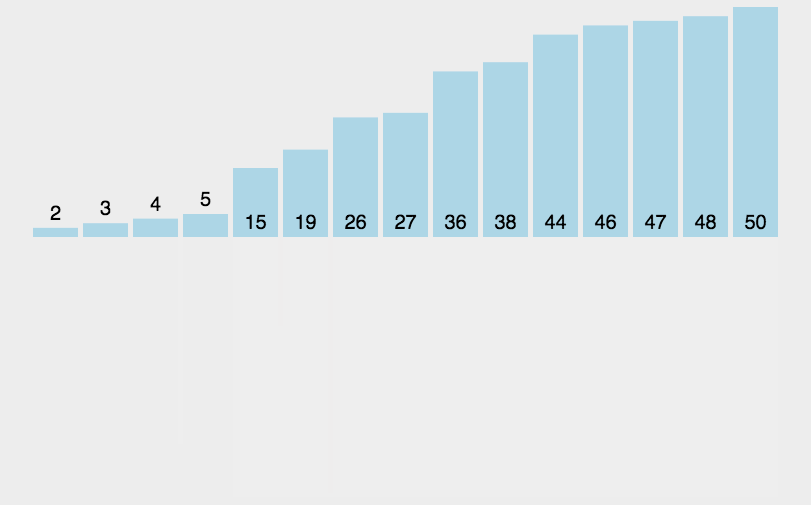
2. 归并---递归版🧚🏻?♀?

2.1 思路分析🪢

递归思想：后序处理，每次返回的时候归并完成了，就有序了

先分割再排序
8->4->2->1 ，1个可以认为是有序的

用到一个新的数组，左区间上先将2个数据拿下来排序，然后再拷贝回去；以此类推将左区间的排完之后，整体排序，然后拷贝回去；以此类推；最后左右区间有序--->按照之前的思路，直接归并

2.2 代码实现🧵

2.2.1 sort.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
// 归并排序递归实现
void MergeSort(int* a, int n);

---

2.2.2 sort.c

#include"sort.h"
// 归并排序递归实现
void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin >= end)//只有1个or不存在时不用排序了
		return;
	int mid = (begin + end) / 2;
	//[begin,mid] [mid+1,end]---分组
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid+1, end, tmp);
	
	//[begin,mid] [mid+1,end]---2组归并
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;//i最好不要赋值为0,因为可能是右区间的归并
	while (begin1 <= end1 && begin2 <= end2)
		//有一个结束了就都结束了
	{
		if (a[begin1] < a[begin2])
			tmp[i++] = a[begin1++];
		else
			tmp[i++] = a[begin2++];
	}
	//可能会有一个区间没有遍历完
	while(begin1<=end1)
		tmp[i++] = a[begin1++];
	while (begin2 <= end2)
		tmp[i++] = a[begin2++];
	//考虑到右区间的拷贝
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
	//为新数组开辟空间
	int* tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		printf("malloc error!\n");
		return;
	}
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}

---

2.2.3 test.c

#include"sort.h"
#include<time.h>
//归并递归版
void testMergeSort()
{
    int a[] = { 3,2,6,8,9,7,5,10,6,1,4 };
    int n = sizeof(a) / sizeof(int);
    MergeSort(a,n);
    PrintArray(a, n);
}
int main()
{
    testMergeSort();
	return 0;
}

---

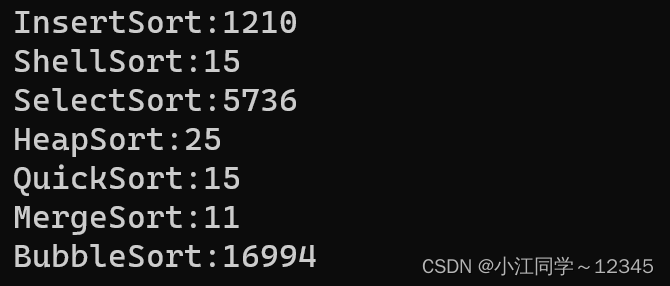
2.3 性能对比🧶

// 测试排序的性能对比
void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
    int* a7 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand()+i;
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
        a7[i] = a1[i];
    }
    int begin1 = clock();
    InsertSort(a1, N);
    int end1 = clock();
    int begin2 = clock();
    ShellSort(a2, N);
    int end2 = clock();
    int begin3 = clock();
    SelectSort(a3, N);
    int end3 = clock();
    int begin4 = clock();
    HeapSort(a4, N);
    int end4 = clock();
    int begin5 = clock();
    QuickSort(a5, 0, N - 1);
    int end5 = clock();
    int begin6 = clock();
    MergeSort(a6, N);
    int end6 = clock();
    int begin7 = clock();
    BubbleSort(a7, N);
    int end7 = clock();
    printf("InsertSort:%d\n", end1 - begin1);
    printf("ShellSort:%d\n", end2 - begin2);
    printf("SelectSort:%d\n", end3 - begin3);
    printf("HeapSort:%d\n", end4 - begin4);
    printf("QuickSort:%d\n", end5 - begin5);
    printf("MergeSort:%d\n", end6 - begin6);
    printf("BubbleSort:%d\n", end7 - begin7);
    free(a1);
    free(a2);
    free(a3);
    free(a4);
    free(a5);
    free(a6);
    free(a7);
}
int main()
{
    TestOP();
	return 0;
}

---

3. 归并---非递归版🧤

3.1 思路分析🎩

1. 归并排序和快排有什么区别？

快排是前序，归并是后序

2. 基于快排非递归是栈实现的，归并用栈实现好不好？

递归实现：归并是在只有1个值的时候返回向上实现排序的

栈实现：大区间先出来，然后划分小区间，请问小区间排完序往哪里返回呢？此时大区间出栈了，没有返回的空间，而且和快排不同，归并并不能像快排一样保证左区间和右区间有序了，整体就有序了，因为归并没有遍历找key分出左右区间（左边均小于key，右边均大于key）；而且快排是最后栈为空之后就整体有序了，不需要返回的直接就排序成功了

3.?递归的分割到底是为了干嘛？

是为了8->4->2->1, 1个不就是有序的嘛

???????

过渡：

就像斐波那契数列一样，递归实现比较麻烦：求n的值，要递归多次n、n-1、n-2......1 1求出n-1的数值才能求出n的数值
循环实现比较简单：求n的数值，直接1+1+......+n-1就求出来了，思路好理解些

新思路：

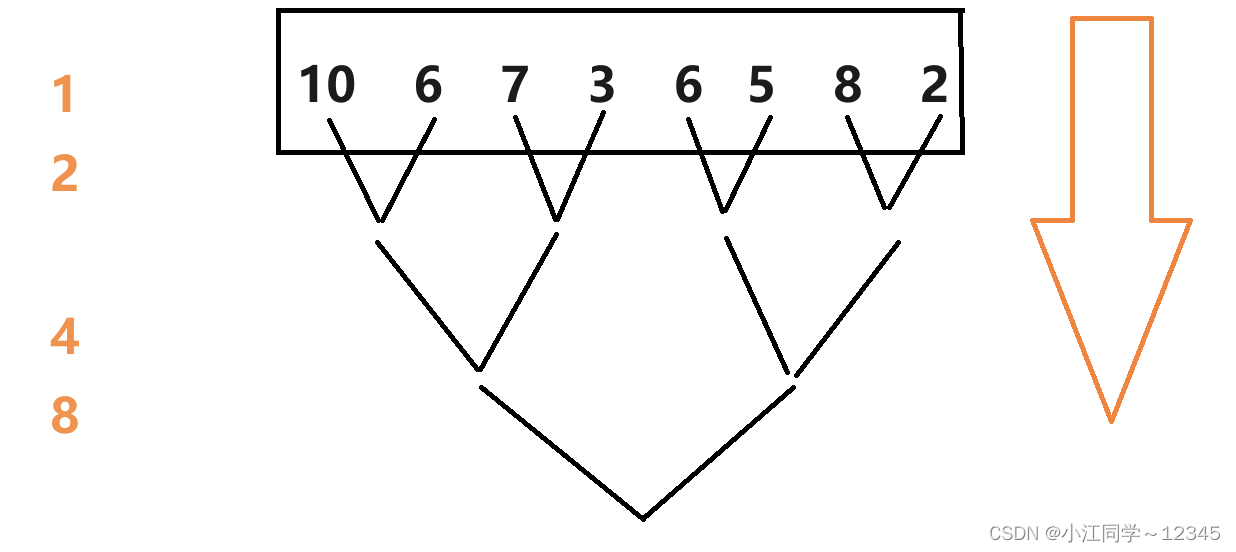
原来递归实现就是倒着走：8->4->2->1
现在新思路就是顺着走：1->2->4->8

---

3.2 代码实现🧢

3.2.1 sort.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
// 归并排序非递归实现
void MergeSortNonR(int* a, int n);

---

3.2.2 sort.c

注意数据个数可能不是2^n，所以这会导致数组分组越界--->判断一下分组是否越界（除了begin1都有可能越界）

例如，我们换一组数据看看：

// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
	//为新数组开辟空间
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc error!\n");
		return;
	}

	//多趟排序
	int gap = 1;//每组数据个数
	while (gap < n)
	{
		//单趟排序
		for (int i = 0; i < n; i += 2 * gap)//i下一次要从end2后面一个开始
		{
			int begin1 = i, end1 = i + gap - 1;//个数-1=下标
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			//判断是否越界
			if (end1 >= n || begin2 >= n)
				break;//如果end1或begin2越界了，那么第二组必定越界，没有归并的必要了
			if (end2 >= n)
				end2 = n - 1;
			//[begin1,end1] [begin2,end2]
			int j = begin1;//i最好不要赋值为0,因为可能是右区间的归并
			while (begin1 <= end1 && begin2 <= end2)
				//有一个结束了就都结束了
			{
				if (a[begin1] < a[begin2])
					tmp[j++] = a[begin1++];
				else
					tmp[j++] = a[begin2++];
			}
			//可能会有一个区间没有遍历完
			while (begin1 <= end1)
				tmp[j++] = a[begin1++];
			while (begin2 <= end2)
				tmp[j++] = a[begin2++];
			//每次归并完（每2组）之后，应当拷贝回数组a
			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i+1));
		}
		gap *= 2;
	}
	free(tmp);
}

---

3.2.3 test.c

#include"sort.h"
//归并非递归版
void testMergeSortNonR()
{
    int a[] = { 3,2,6,8,9,7,5,10,6,1,4 };
    int n = sizeof(a) / sizeof(int);
    MergeSortNonR(a, n);
    PrintArray(a, n);
}
int main()
{
    testMergeSortNonR();
	return 0;
}

---

4.?归并排序的特性总结

1.?归并的缺点在于需要O(N)的空间复杂度

2.?时间复杂度：O(N*logN)

3.?空间复杂度：O(N)

4.?稳定性：稳定

---

5. 非比较排序---计数排序👔

5.1 基本思想👑

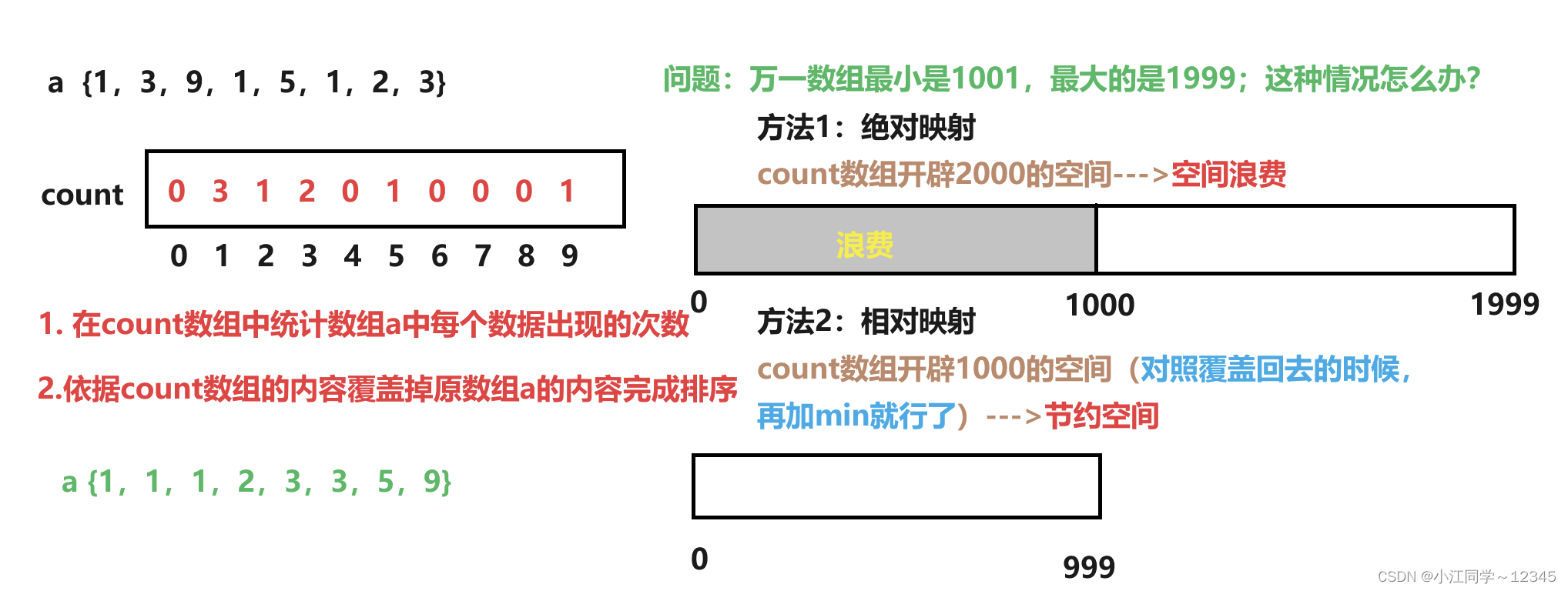
思想：计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。 操作步骤：

1.?统计相同元素出现次数

2.?根据统计的结果将序列回收到原来的序列中

绝对映射不可以解决负数排序但是相对映射可以解决（可以自己带数看看）

---

5.2 思路分析🐹

---

5.3?代码实现🐸

5.3.1 sort.h

// 计数排序
void CountSort(int* a, int n);

---

5.3.2 sort.c

// 计数排序
void CountSort(int* a, int n)
{
	//遍历找出最大和最小
	int min = a[0], max = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] > max)
			max = a[i];
		if (a[i] < min)
			min = a[i];
	}
	//设置count数组范围
	int range = max - min+1;//[ ]+1
	//开辟空间
	int* count = (int*)calloc(range, sizeof(int));
	if (count == NULL)
	{
		printf("calloc error!\n");
		return;
	}
	//统计次数
	for (int i = 0; i < n; i++)
		count[a[i] - min]++;
	//覆盖回去
	int i = 0;
	for (int j = 0; j < range; j++)
	{
		while (count[j]--)//有几个相同的数据
			a[i++] = j + min;
	}
}

---

5.3.3 test.c

//计数排序
void testCountSort()
{
    int a[] = { 3,2,6,8,9,7,3,5,7,10,6,1,7,4 };
    int n = sizeof(a) / sizeof(int); 
    CountSort(a,n);
    PrintArray(a, n);
}
int main()
{
    testCountSort();
	return 0;
}

---

---

5.4 性能对比

#include"sort.h"
#include<time.h>
// 测试排序的性能对比
void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
    int* a7 = (int*)malloc(sizeof(int) * N);
    int* a8 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand()+i;
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
        a7[i] = a1[i];
        a8[i] = a1[i];
    }
    int begin1 = clock();
    InsertSort(a1, N);
    int end1 = clock();
    int begin2 = clock();
    ShellSort(a2, N);
    int end2 = clock();
    int begin3 = clock();
    SelectSort(a3, N);
    int end3 = clock();
    int begin4 = clock();
    HeapSort(a4, N);
    int end4 = clock();
    int begin5 = clock();
    QuickSort(a5, 0, N - 1);
    int end5 = clock();
    int begin6 = clock();
    MergeSort(a6, N);
    int end6 = clock();
    int begin7 = clock();
    BubbleSort(a7, N);
    int end7 = clock(); 
    int begin8 = clock();
    CountSort(a8, N);
    int end8 = clock();
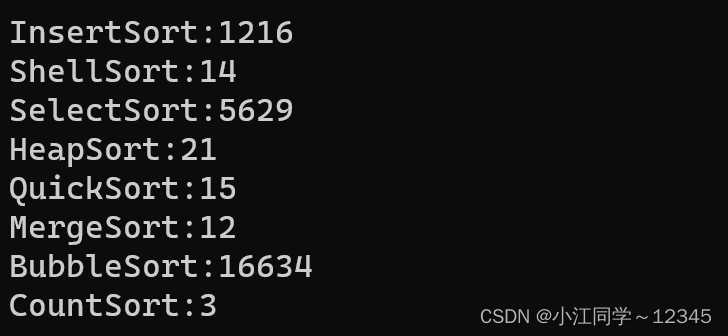
    printf("InsertSort:%d\n", end1 - begin1);
    printf("ShellSort:%d\n", end2 - begin2);
    printf("SelectSort:%d\n", end3 - begin3);
    printf("HeapSort:%d\n", end4 - begin4);
    printf("QuickSort:%d\n", end5 - begin5);
    printf("MergeSort:%d\n", end6 - begin6);
    printf("BubbleSort:%d\n", end7 - begin7);
    printf("CountSort:%d\n", end8 - begin8);
    free(a1);
    free(a2);
    free(a3);
    free(a4);
    free(a5);
    free(a6);
    free(a7);
    free(a8);
}
int main()
{
    TestOP();
	return 0;
}

---

6. 计数排序特性总结🐯

计数排序的特性总结：

1.?计数排序在数据范围集中时，效率很高，但是适用范围及场景有限：只适合整数

2.?时间复杂度：O(MAX(N,范围))

3.?空间复杂度：O(范围)

---

7.?排序算法复杂度及稳定性分析🐲

排序	时间	空间	稳定性
直接插入排序	O(N^2)	O(1)	稳定
希尔排序	O(N^1.3)	O(1)	不稳定
选择排序	O(N^2)	O(1)	不稳定
堆排序	O(N*logN)	O(1)	不稳定
冒泡排序	O(N^2)	O(1)	稳定
快速排序	O(N*logN)	O(logN)	不稳定
归并排序	O(N*logN)	O(N)	稳定

---

后语🤡

到这里，我们排序的章节就结束了！C也告一段落了。接下来我将持续更新C++的初阶内容，希望大家多多支持！！！

---

本次的分享到这里就结束了！！！

PS：小江目前只是个新手小白。欢迎大家在评论区讨论哦！有问题也可以讨论的！期待大家的互动！！！

公主/王子殿下，请给我点赞👍+收藏??+关注?（这对我真的很重要！！！）

---