菜鸟之MATLAB学习——SSB & DSB调制信号及其频谱分析

clc;
close all;


fm=1;
fc=10;
dt=0.001;
T=5;
t=0:dt:T-dt;
A=2;

mt=A*cos(2*pi*fm*t);
s_ssb=real(hilbert(mt).*exp(j*2*pi*fc*t)); 
s_dsb=mt.*cos(2*pi*fc*t);
B=fm;
subplot(311),plot(t,s_ssb);

fs=1/dt;
N=T/dt;
df=fs/N;

%%%%------- ssb信号的傅里叶变换---------%%%%

f=0:df:(N-1)*df;
sf_ssb=fft(s_ssb);
sf_ssb=fftshift(sf_ssb);
f=f-N/2*df;

%%%%------- ------end-----------------%%%%

%%-------------DSB的傅里叶变换-----------%%%%
sf_dsb=fft(s_dsb);
sf_dsb=fftshift(sf_dsb);
subplot(312),plot(f,1/N*real(sf_dsb));
axis([-20,20,0,1]);
xlabel('dsb fft');
%%%%------- mt傅里叶变换---------%%%%
mtf=fft(mt);
mtf=fftshift(mtf);
subplot(313),plot(f,1/N*real(mtf));hold on;

plot(f,1/N*sf_ssb,'r--');
axis([-20,20,0,1]);
xlabel('ssb fft');

运行结果

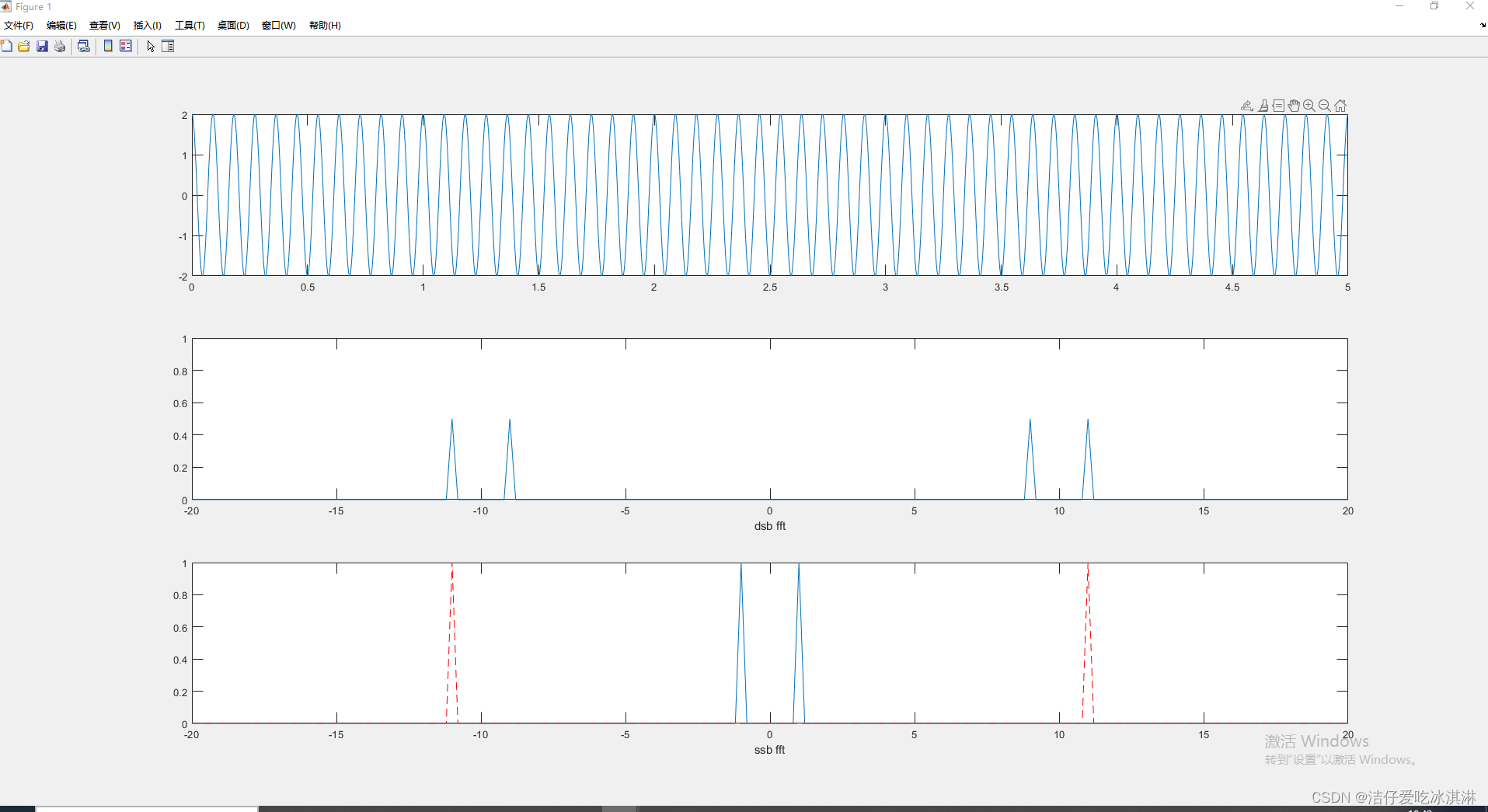
值得注意的是：
hilbert(x)是对实信号求其解析信号，即实部为实信号，虚部为其希尔伯特变换后的信号。

从FFT变换后的幅值来讲，SSB是其DSB的两倍，原因是解析信号的能量是实信号的两倍。