LeetCode刷题--- 不同路径

个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

个人专栏

力扣递归算法题

?http://t.csdnimg.cn/yUl2I

【C++】? ??

??????http://t.csdnimg.cn/6AbpV

数据结构与算法

????http://t.csdnimg.cn/hKh2l

前言：这个专栏主要讲述动态规划算法，所以下面题目主要也是这些算法做的 ?

我讲述题目会把讲解部分分为3个部分：
1、题目解析

2、算法原理思路讲解

3、代码实现

不同路径

题目链接：不同路径

题目

一个机器人位于一个?m x n?网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

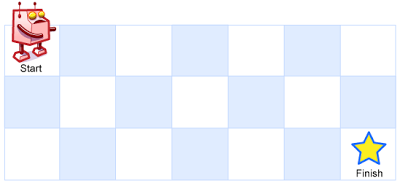
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于?2 * 109

解法

题目解析

1. 一个机器人位于一个?m x n?网格的左上角 （起始点在下图中标记为 “Start” ）。
2. 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角。
3. 总共有多少条不同的路径。

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

算法原理讲解

我们这题使用动态规划，我们做这类题目可以分为以下五个步骤

1. 状态显示
2. 状态转移方程
3. 初始化（防止填表时不越界）
4. 填表顺序
5. 返回值

• 状态显示

????????dp[i][j] 表示：?到 [i, j] 位置处，?共有多少种方式。

• 状态转移方程

• 从 [i, j] 位置的上?（ [i - 1, j] 的位置）向下??步，转移到 [i, j] 位置；
• 从 [i, j] 位置的左?（ [i, j - 1] 的位置）向右??步，转移到 [i, j] 位置。

• 初始化（防止填表时不越界）

• 辅助结点??的值要「保证后续填表是正确的」；
• 「下标的映射关系」。

• 填表顺序

• 返回值

class Solution 
{
public:
    int uniquePaths(int m, int n) 
    {
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0)); // 创建?个 dp表
        dp[0][1] = 1; // 初始化
        
        // 填表
        for (int i = 1; i <= m; i++) // 从上往下
        {
            for (int j = 1; j <= n; j++) // 从左往右
            {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        // 返回结果
        return dp[m][n];
    }   
};