机器学习_梯度下降

什么是梯度

计算梯度向量其几何意义，就是函数变化的方向，而且是变化最快的方向。对于函数f(x)，在点(xo,yo)，梯度向量的方向也就是y值增加最快的方向。也就是说，沿着梯度向量的方向 △f(xo)，能找到函数的最大值。反过来说，沿着梯度向量相反的方向，也就是 -△f(xo)的方向，梯度减少最快，能找到函数的最小值。如果某一个点的梯度向量的值为0，那么也就是来到了导数为0的函数最低点(或局部最低点)了。

梯度下降

下山的路上，难免会出现一会下坡，一会上坡，直到走到山下。

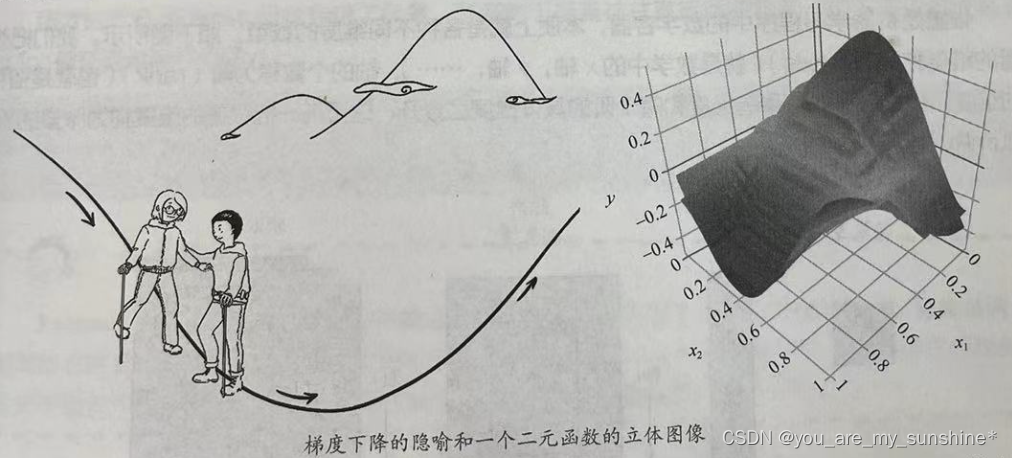
从上面的解释中，就不难理解为何刚才我们要提到函数的凹凸性了。因为，在非凸函数中，有可能还没走到山脚，而是到了某一个山谷就停住了。也就是说，对应非凸函数梯度下降不一定总能够找到全局最优解，有可能得到的只是一个局部最优解。然而，如果函数是凸函数，那么梯度下降法理论上就能得到全局最优解。

梯度下降有什么用

梯度下降在机器学习中非常有用。简单地说，可以注意以下几点。

• 机器学习的本质是找到最优的函数。
• 如何衡量函数是否最优?其方法是尽量减小预测值和真值间的误差(在机器学习中也叫损失值)。
• 可以建立误差和模型参数之间的函数(最好是凸函数)。
• 梯度下降能够引导我们走到凸函数的全局最低点，也就是找到误差最小时的参数。

学习机器学习的参考资料：
（1）书籍
利用Python进行数据分析
西瓜书
百面机器学习
机器学习实战
阿里云天池大赛赛题解析(机器学习篇)
白话机器学习中的数学
零基础学机器学习
图解机器学习算法
…

（2）机构
光环大数据
开课吧
极客时间
七月在线
深度之眼
贪心学院
拉勾教育
博学谷
…