【数学建模】《实战数学建模:例题与讲解》第十二讲-因子分析、判别分析(含Matlab代码)
【数学建模】《实战数学建模:例题与讲解》第十二讲-因子分析、判别分析(含Matlab代码)
本系列侧重于例题实战与讲解,希望能够在例题中理解相应技巧。文章开头相关基础知识只是进行简单回顾,读者可以搭配课本或其他博客了解相应章节,然后进入本文正文例题实战,效果更佳。
如果这篇文章对你有帮助,欢迎点赞与收藏~

基本概念
判别分析是一种统计方法,它根据所研究的个体的观测指标来推断该个体所属类型。在自然科学和社会科学的研究中经常会碰到这种统计问题。例如,质找矿中要根据某异常点的地质结构、化探和物探的各项指标来判断该异常点属于哪种矿化类型;医生要根据某人的各项化验指标的结果来判断属于什么病症;调查某地区的土生产率、劳动生产率、人均收入、费用水平、农村工业比例指标,确定该地区属于哪种经济类型区等。
判别分析的目的是对已知分类的数据建立由数值指标构成的分类规则,然后把这样的规则应用到未知分类的样本去分类。例如,我们有了患胃炎的病人和健康人的一些化验指标,就可以从这些化验指标发现两类人的区别,把这种区别表示为一个判别公式,然后对怀疑患胃炎的人就可以根据其化验指标用判别公式诊断。
判别分析的方法按照判别的组数来区分,可以分为两组判别分析和多组判别分析。判别分析中,根据资料的性质,分为定性资料的判别分析和定量资料的判别分析;采用不同的判别准则,又有费歇、贝叶斯、距离等判别方法。
时间判别
时间判别是一种判别分析方法,它是根据时间序列的特征来判断时间序列所属的类别。时间序列是指按时间顺序排列的一组数据,它是一种重要的数据类型,广泛应用于金融、经济、气象、环境、医学等领域。时间判别的方法有很多,例如,基于时间序列的自回归模型、移动平均模型、ARMA模型等。
费歇判别
Fisher判别是一种线性判别方法,它是根据样本的特征向量来判断样本所属的类别。Fisher判别的基本思想是投影,使多维问题简化为一维问题来处理。选择一个适当的投影轴,使所有的样品点都投影到这个轴上得到一个投影值。对这个投影轴的方向的要求是:使每一类内的投影值所形成的类内离差尽可能小,而不同类间的投影值所形成的类间离差尽可能大。
贝叶斯判别
贝叶斯判别是一种概率判别方法,它是根据贝叶斯定理来判断样本所属的类别。贝叶斯判别的基本思想是,对于给定的样本,计算它属于每个类别的后验概率,然后将样本判给后验概率最大的那个类别。贝叶斯判别的方法有很多,例如,朴素贝叶斯分类、高斯混合模型等。
习题10.3
1. 题目要求
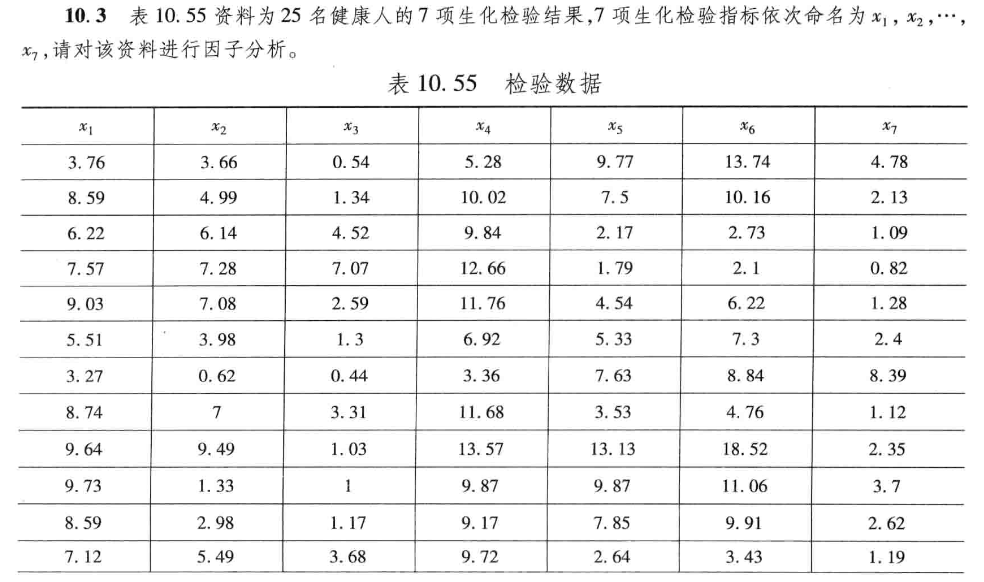
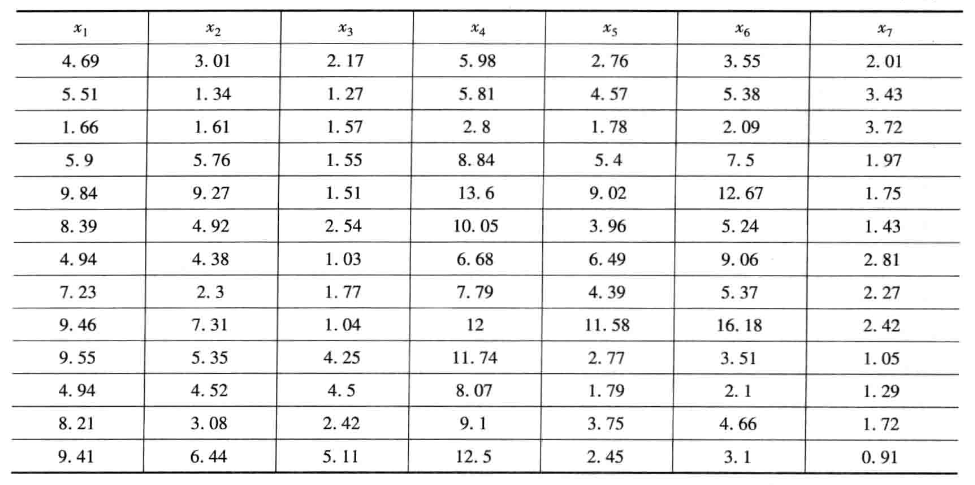
2.解题过程
解:
先将数据标准化,记第
i
i
i 个评价对象的第
j
j
j 个评价指标值为
a
i
j
,
i
=
1
,
2
,
.
.
.
25
;
j
=
1
,
2
,
.
.
.
7
a_{ij},i=1,2,...25;j=1,2,...7
aij?,i=1,2,...25;j=1,2,...7 ,将
a
i
j
a_{ij}
aij? 标准化为
a
~
i
j
\widetilde{a}_{ij}
a
ij? :
a
~
i
j
=
a
i
j
?
μ
j
s
j
\widetilde{a}_{ij}=\frac{a_{ij}-\mu_j}{s_j}
a
ij?=sj?aij??μj??
式中:
μ
j
=
1
25
∑
i
=
1
25
a
i
j
\mu_j=\frac{1}{25}\sum_{i=1}^{25}a_{ij}
μj?=251?i=1∑25?aij?
s j = 1 25 ? 1 ∑ i = 1 25 ( a i j ? μ j ) 2 s_j=\sqrt{\frac{1}{25-1}\sum_{i=1}^{25}(a_{ij}-\mu_j)^2} sj?=25?11?i=1∑25?(aij??μj?)2?
接下来计算相关系数矩阵
R
\mathbf{R}
R :
R
=
(
r
i
j
)
7
×
7
\mathbf{R}=(r_{ij})_{7\times7}
R=(rij?)7×7?
r i j = ∑ k = 1 25 a ~ k i ? a ~ k j , i , j = 1 , 2 , . . . , 7 r_{ij}=\frac{\sum_{k=1}^{25}}{\widetilde{a}_{ki}\cdot\widetilde{a}_{kj}},i,j=1,2,...,7 rij?=a ki??a kj?∑k=125??,i,j=1,2,...,7
式中 r i i = 1 , r j i = r i j , r i j r_{ii}=1,r_{ji}=r{ij},r_{ij} rii?=1,rji?=rij,rij? 是第 i i i 指标和第 j j j 指标的相关系数。
计算初等载荷矩阵,首先算出相关矩阵
R
\mathbf{R}
R 的特征值
λ
1
≥
λ
2
≥
.
.
.
≥
λ
7
\lambda_1\geq\lambda_2\geq...\geq\lambda_7
λ1?≥λ2?≥...≥λ7?,以及应的特征向量
u
1
,
u
2
,
.
.
.
,
u
7
\mathbf{u}_1,\mathbf{u}_2,...,\mathbf{u}_7
u1?,u2?,...,u7?,则初等载荷矩阵为:
Λ
1
=
[
λ
1
u
1
,
λ
1
u
2
,
.
.
.
,
λ
1
u
7
]
\mathbf{\Lambda}_1=[\sqrt{\lambda_1}\mathbf{u}_1,\sqrt{\lambda_1}\mathbf{u}_2,...,\sqrt{\lambda_1}\mathbf{u}_7]
Λ1?=[λ1??u1?,λ1??u2?,...,λ1??u7?]
计算得出前三个特征值的贡献率达到了
98
%
98\%
98% ,选择三个主因子,对提取的因子载荷矩阵进行旋转,得到矩阵
Λ
2
=
Λ
1
(
3
)
T
\mathbf{\Lambda}_2=\mathbf{\Lambda}^{(3)}_1\mathbf{T}
Λ2?=Λ1(3)?T ,
取
Λ
1
\mathbf{\Lambda}_1
Λ1?的前三列,
T
\mathbf{T}
T为正交矩阵,构造因子模型:
{
x
~
1
=
α
11
F
~
1
+
α
12
F
~
2
+
α
13
F
~
3
?
x
~
7
=
α
71
F
~
1
+
α
72
F
~
2
+
α
73
F
~
3
\begin{align*} \begin{cases} \widetilde{x}_1=\alpha_{11}\widetilde{F}_1+\alpha_{12}\widetilde{F}_2+\alpha_{13}\widetilde{F}_3 \\ \vdots\\ \widetilde{x}_7=\alpha_{71}\widetilde{F}_1+\alpha_{72}\widetilde{F}_2+\alpha_{73}\widetilde{F}_3 \end{cases} \end{align*}
?
?
??x
1?=α11?F
1?+α12?F
2?+α13?F
3??x
7?=α71?F
1?+α72?F
2?+α73?F
3???
最终,得到了三个因子,第一个因子是
x
1
x_1
x1? ,第二个因子是
x
5
x_5
x5? ,第三个因子是
x
2
x_2
x2? 。
3.程序
求解的MATLAB程序如下:
clc, clear
% 给定的原始数据矩阵
dd = [3.76, 3.66, 0.54, 5.28, 9.77, 13.74, 4.78; ...
8.59, 4.99, 1.34, 10.02, 7.5, 10.16, 2.13; ...
6.22, 6.14, 4.52, 9.84, 2.17, 2.73, 1.09; ...
7.57, 7.28, 7.07, 12.66, 1.79, 2.1, 0.82; ...
9.03, 7.08, 2.59, 11.76, 4.54, 6.22, 1.28; ...
5.51, 3.98, 1.3, 6.92, 5.33, 7.3, 2.4; ...
3.27, 0.62, 0.44, 3.36, 7.63, 8.84, 8.39; ...
8.74, 7, 3.31, 11.68, 3.53, 4.76, 1.12; ...
9.64, 9.49, 1.03, 13.57, 13.13, 18.52, 2.35; ...
9.73, 1.33, 1, 9.87, 9.87, 11.06, 3.7; ...
8.59, 2.98, 1.17, 9.17, 7.85, 9.91, 2.62; ...
7.12, 5.49, 3.68, 9.72, 2.64, 3.43, 1.19; ...
4.69, 3.01, 2.17, 5.98, 2.76, 3.55, 2.01; ...
5.51, 1.34, 1.27, 5.81, 4.57, 5.38, 3.43; ...
1.66, 1.61, 1.57, 2.8, 1.78, 2.09, 3.72; ...
5.9, 5.76, 1.55, 8.84, 5.4, 7.5, 1.97; ...
9.84, 9.27, 1.51, 13.6, 9.02, 12.67, 1.75; ...
8.39, 4.92, 2.54, 10.05, 3.96, 5.24, 1.43; ...
4.94, 4.38, 1.03, 6.68, 6.49, 9.06, 2.81; ...
7.23, 2.3, 1.77, 7.79, 4.39, 5.37, 2.27; ...
9.46, 7.31, 1.04, 12, 11.58, 16.18, 2.42; ...
9.55, 5.35, 4.25, 11.74, 2.77, 3.51, 1.05; ...
4.94, 4.52, 4.5, 8.07, 1.79, 2.1, 1.29; ...
8.21, 3.08, 2.42, 9.1, 3.75, 4.66, 1.72; ...
9.41, 6.44, 5.11, 12.5, 2.45, 3.1, 0.91];
% 标准化数据(Z-score标准化)
stdd = zscore(dd);
% 计算标准化数据的相关系数矩阵
r = corrcoef(stdd);
% 使用PCA对相关系数矩阵进行主成分分析,获取特征向量(vec1)、特征值(val)和贡献率(con)
[vec1, val, con] = pcacov(r);
% 计算符号矩阵f1,其大小与vec1一致,元素值均为vec1所有元素的和的符号
f1 = repmat(sign(sum(vec1)), size(vec1, 1), 1);
% 将特征向量(vec1)与符号矩阵(f1)相乘,得到新的特征向量矩阵(vec2)
vec2 = vec1 .* f1;
% 计算矩阵f2,其大小与vec2一致,元素值均为val中的特征值的平方根
f2 = repmat(sqrt(val)', size(vec2, 1), 1);
% 将vec2与f2相乘,得到最终的载荷矩阵(a)
a = vec2 .* f2;
% 设定保留的主成分数目
num = 3;
% 保留前num个主成分
am = a(:, [1:num]);
% 使用varimax方法对主成分进行旋转,获得旋转后的载荷矩阵(b)以及得分矩阵(t)
[b, t] = rotatefactors(am, 'Method', 'varimax');
% 将未保留的主成分载荷也加入旋转后的载荷矩阵,得到旋转后的完整载荷矩阵(bt)
bt = [b, a(:, [num + 1:end])];
% 计算每个变量在各个主成分上的载荷的平方和,得到公共度(degree)
degree = sum(b.^2, 2);
% 计算每个主成分的总的贡献率(contr)
contr = sum(bt.^2);
% 计算被保留的主成分的累计贡献率(rate)
rate = contr(1:num) / sum(contr);
% 计算因子分析的系数矩阵(coef)
coef = inv(r) * b;
4.结果

得到的因子分析表如下:
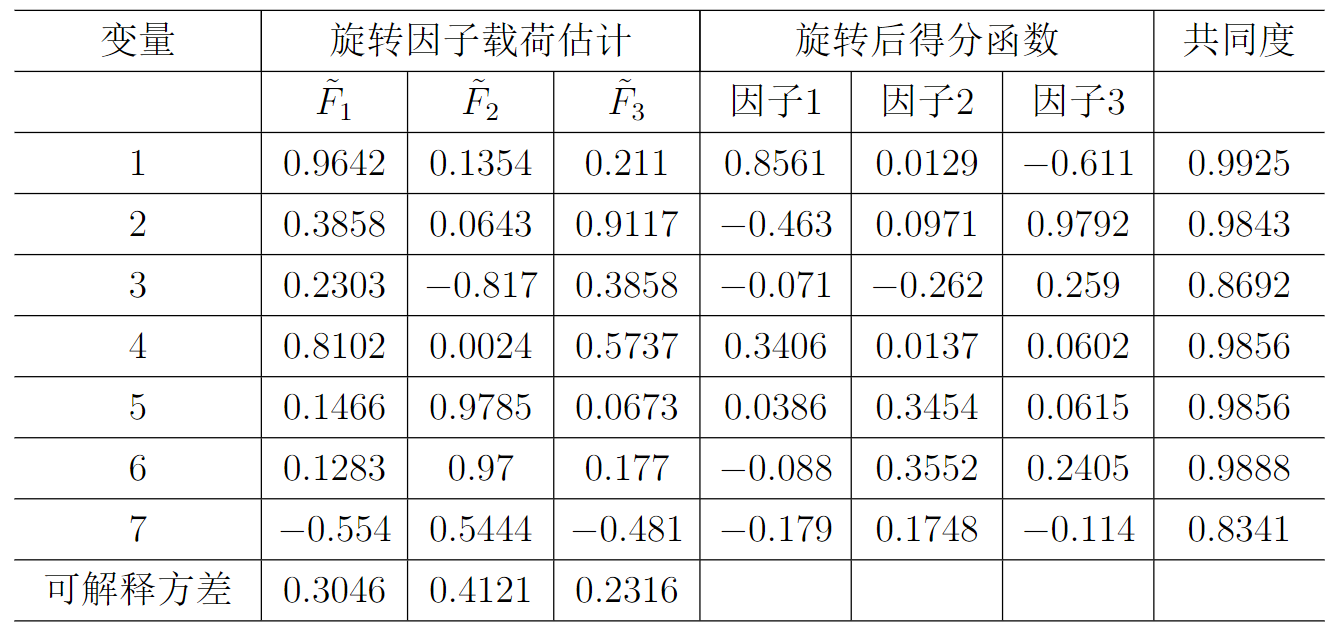
得到了三个因子,第一个因子是 x 1 x_1 x1? ,第二个因子是 x 5 x_5 x5? ,第三个因子是 x 2 x_2 x2? 。
习题10.6(1)
1. 题目要求
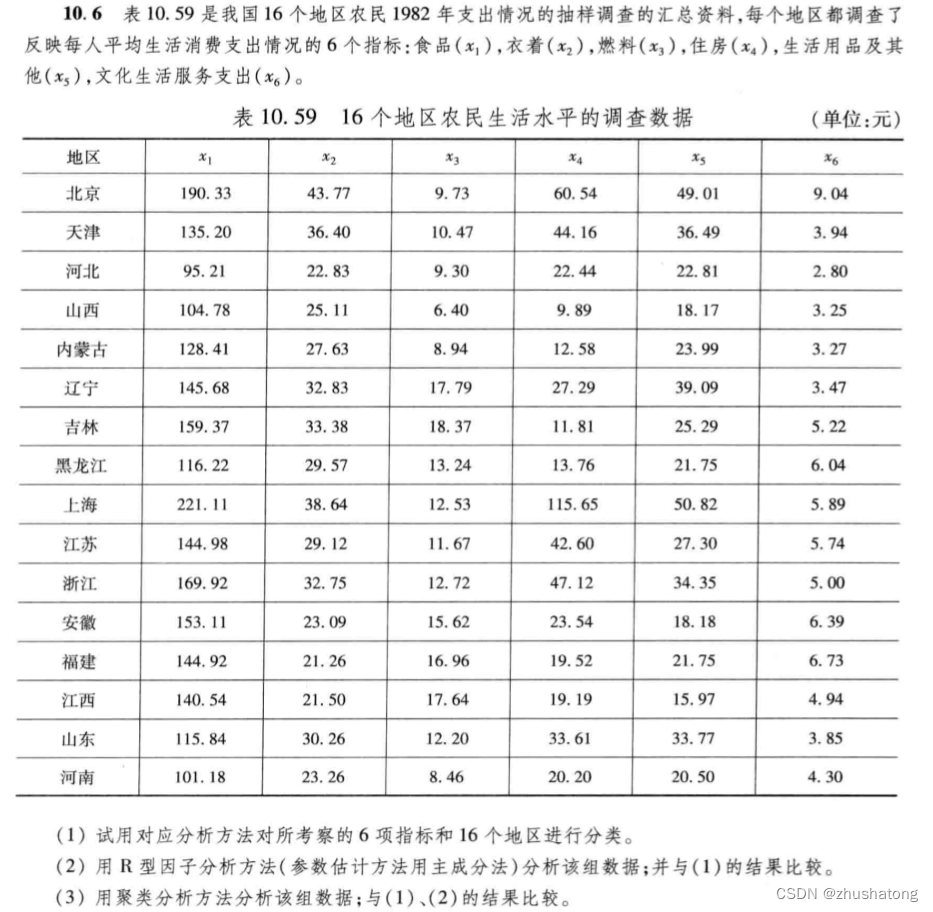
2.解题过程——对应分析
解:
分别用 i = 1 , … , 16 i=1,\dots,16 i=1,…,16 表示,以 a i j a_{ij} aij? 表示第 i 个地区第 j 个指标变量 x j x_j xj? 的取值。
记:
A
=
(
a
i
j
)
16
×
6
\mathbf{A}=(a_{ij})_{16\times6}
A=(aij?)16×6?
记:
a
i
?
=
∑
j
=
1
6
a
i
j
,
a
?
j
=
∑
i
=
1
16
a
i
j
a_{i\cdot}=\sum_{j=1}^{6}a_{ij},a_{\cdot j}=\sum_{i=1}^{16}a_{ij}
ai??=j=1∑6?aij?,a?j?=i=1∑16?aij?
首先把
A
\mathbf{A}
A 化为规格化的“概率”矩阵
P
\mathbf{P}
P , 记
P
=
(
p
i
j
)
16
×
6
\mathbf{P}=(p_{ij})_{16\times6}
P=(pij?)16×6? ,其中
p
i
j
=
a
i
j
/
T
p_{ij}=a_{ij}/\mathbf{T}
pij?=aij?/T ,
T
=
∑
i
=
1
16
∑
j
=
1
6
a
i
j
\mathbf{T}=\sum_{i=1}^{16}\sum_{j=1}^{6}a_{ij}
T=∑i=116?∑j=16?aij?。再对数据进行对应变换,令
B
=
(
b
i
j
)
16
×
6
\mathbf{B}=(b_{ij})_{16\times6}
B=(bij?)16×6? ,其中:
b
i
j
=
p
i
j
?
p
i
?
p
?
j
p
i
?
p
?
j
=
a
i
j
?
a
i
?
a
?
j
/
T
a
i
?
a
?
j
,
i
=
1
,
2
,
…
,
16
,
j
=
1
,
2
,
…
,
6.
b_{ij}=\frac{p_{ij}-p_{i\cdot}p_{\cdot j}}{\sqrt{p_{i\cdot}p_{\cdot j}}} = \frac{a_{ij}-a_{i\cdot}a_{\cdot j}/\mathbf{T}}{\sqrt{a_{i\cdot}a_{\cdot j}}}, i=1,2,\dots, 16,j=1,2,\dots,6.
bij?=pi??p?j??pij??pi??p?j??=ai??a?j??aij??ai??a?j?/T?,i=1,2,…,16,j=1,2,…,6.
对
B
\mathbf{B}
B 进行奇异值分解,
B
=
U
Λ
V
T
\mathbf{B}=\mathbf{U}\varLambda \mathbf{V}^{\mathbf{T}}
B=UΛVT,其中
U
\mathbf{U}
U 为
16
×
16
16\times 16
16×16 正交矩阵,
V
\mathbf{V}
V为
6
×
6
6\times6
6×6 正交矩阵,
Λ
=
[
Λ
m
0
0
0
]
\varLambda =\begin{bmatrix} \varLambda_m &0\\ 0&0 \end{bmatrix}
Λ=[Λm?0?00?],这里
Λ
m
=
d
i
a
g
(
d
1
,
…
,
d
m
)
\varLambda_m=diag(d_1,\dots,d_m)
Λm?=diag(d1?,…,dm?) ,其中
d
i
(
i
=
1
,
2
,
…
,
m
)
d_i(i=1,2,\dots,m)
di?(i=1,2,…,m) 为
B
\mathbf{B}
B 的奇异值。
记 U = [ U 1 ? U 2 ] , V = [ V 1 ? V 2 ] \mathbf{U}=[\mathbf{U_1} \vdots \mathbf{U_2}],\mathbf{V}=[\mathbf{V_1} \vdots \mathbf{V_2}] U=[U1??U2?],V=[V1??V2?] ,其中 U 1 \mathbf{U_1} U1? 为 16 × m 16\times m 16×m 的列正交矩阵, V 1 \mathbf{V_1} V1? 为 6 × m 6\times m 6×m 的列正交矩阵,则 B \mathbf{B} B 的奇异值分解式等价于 B = U 1 Λ V 1 T \mathbf{B}=\mathbf{U_1}\varLambda\mathbf{V_1}^T B=U1?ΛV1?T。
记 D r = d i a g ( p 1 ? , p 2 ? , … , p 16 ? ) , D c = d i a g ( p ? 1 , p ? 2 , … , p ? 6 ) \mathbf{D_r}=diag(p_{1\cdot},p_{2\cdot},\dots,p_{16\cdot}),\mathbf{D_c}=diag(p_{\cdot1},p_{\cdot2},\dots,p_{\cdot6}) Dr?=diag(p1??,p2??,…,p16??),Dc?=diag(p?1?,p?2?,…,p?6?) ,其中 p i ? = ∑ j = 1 6 p i j p_{i\cdot}=\sum_{j=1}^{6}p_{ij} pi??=∑j=16?pij? , p ? j = ∑ i = 1 16 p i j p_{\cdot j}=\sum_{i=1}^{16}p_{ij} p?j?=∑i=116?pij?。则列轮廓的坐标为 F = D c ? 1 / 2 V 1 Λ m \mathbf{F}=\mathbf{D}_{c}^{-1/2}\mathbf{V_1}\varLambda_m F=Dc?1/2?V1?Λm? ,行轮廓的坐标为 G = D r ? 1 / 2 V 1 Λ m \mathbf{G}=\mathbf{D}_{r}^{-1/2}\mathbf{V_1}\varLambda_m G=Dr?1/2?V1?Λm? 。最后通过贡献率的比较确定需要截取的维数,形成对应分析图。
计算 B T B \mathbf{B^T}\mathbf{B} BTB 的特征值,惯量,表示相应维数对各类别的解释量,最大维数 m = min ? 16 ? 1 , 6 ? 1 m=\min{16-1,6-1} m=min16?1,6?1 ,本例最多可以产生5个维数。从下表可看出,第一维数的解释量达 77.4% ,前两个维数的解释度已达92.1%。
| 维数 | 奇异值 | 惯量 | 贡献率 | 累积贡献率 |
|---|---|---|---|---|
| 1 | 0.189893 | 0.036059 | 0.773764 | 0.773764 |
| 2 | 0.082831 | 0.006861 | 0.147224 | 0.920988 |
| 3 | 0.047138 | 0.002222 | 0.047618 | 0.968669 |
| 4 | 0.03113 | 0.000969 | 0.020795 | 0.989464 |
| 5 | 0.022159 | 0.000491 | 0.010536 | 1 |
行坐标
| 北京 | 天津 | 河北 | 山西 | 内蒙古 | 辽宁 | |
|---|---|---|---|---|---|---|
| 第一维 | -0.07905 | -0.06783 | -0.26354 | 0.457766 | 0.07715 | -0.13567 |
| 第二维 | -0.0354 | 0.138818 | -0.10045 | -0.05715 | 0.156316 | -0.08455 |
| 吉林 | 黑龙江 | 上海 | 江苏 | 浙江 | 安徽 | |
|---|---|---|---|---|---|---|
| 第一维 | -0.27126 | -0.19757 | 0.386809 | 0.086955 | 0.079122 | -0.14212 |
| 第二维 | -0.00074 | 0.045985 | -0.07833 | -0.04222 | -0.01969 | -0.14225 |
| 福建 | 江西 | 山东 | 河南 | |
|---|---|---|---|---|
| 第一维 | -0.17469 | -0.18859 | 0.069823 | -0.1462 |
| 第二维 | -0.11317 | -0.1527 | 0.100318 | 0.032858 |
列坐标
| x1 | x2 | x3 | x4 | x5 | x6 | |
|---|---|---|---|---|---|---|
| 第一维 | -0.07905 | -0.06783 | -0.26354 | 0.457766 | 0.07715 | -0.13567 |
| 第二维 | -0.0354 | 0.138818 | -0.10045 | -0.05715 | 0.156316 | -0.08455 |
在下图中,给出16个地区和6个指标在相同坐标系上绘制的散布图。
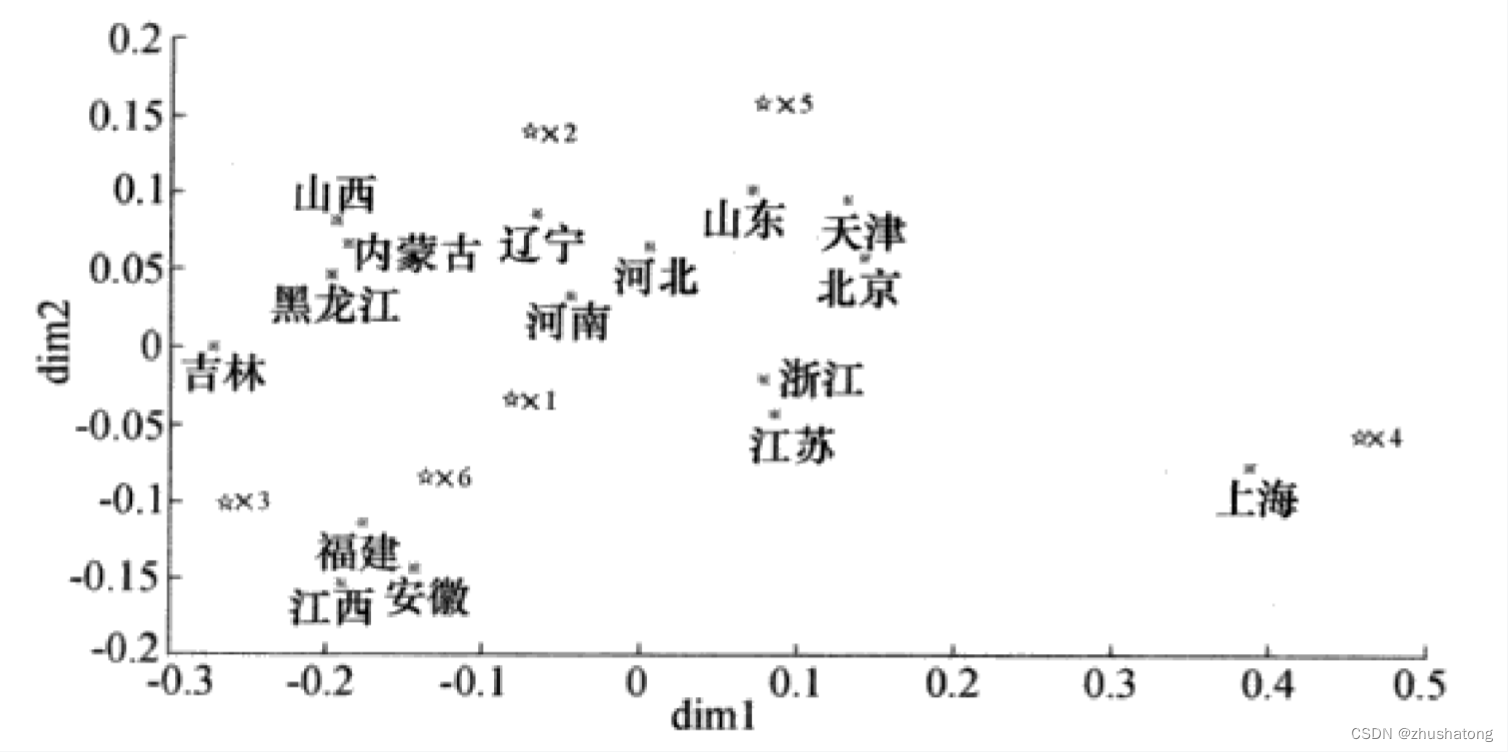
从图中可以看出,地区和指标点可以分为两类,
第一类包括指标点 x 4 , x 5 x_4,x_5 x4?,x5? ,地区点为北京、天津、河北、上海、江苏、浙江、山东;
第二类包括指标点 x 1 , x 2 , x 3 , x 6 x_1,x_2,x_3,x_6 x1?,x2?,x3?,x6? ,地区点为其余地区。
3.程序
求解的MATLAB程序如下:
clc, clear
% 原始数据,其中包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
101.18, 23.26, 8.46, 20.20, 20.50, 4.30];
% 计算原始数据的总和
totalSum = sum(sum(originalData));
% 计算原始数据的比例
ratioData = originalData / totalSum;
% 计算行和列的比例
rowRatio = sum(ratioData, 2);
columnRatio = sum(ratioData);
% 计算行剖面数据
Row_prifile = originalData ./ repmat(sum(originalData, 2), 1, size(originalData, 2));
% 计算B(B为对应分析的基础矩阵)
B = (ratioData - rowRatio * columnRatio) ./ sqrt(rowRatio*columnRatio);
% 对B矩阵进行奇异值分解,得到U,S,V矩阵
[U, S, V] = svd(B, 'econ');
% 对V矩阵列求和并根据其符号调整权重
W1 = sign(repmat(sum(V), size(V, 1), 1));
% 对U矩阵列求和并根据其符号调整权重
W2 = sign(repmat(sum(V), size(U, 1), 1));
% 应用权重调整V和U矩阵
V_adjusted = V .* W1;
U_adjusted = U .* W2;
% 计算lambda(特征值的平方)
lambda = diag(S).^2;
% 计算卡方统计量
chi2Square = totalSum * (lambda);
% 计算总的卡方统计量
totalChi2Square = sum(chi2Square);
% 计算贡献率
contributionRate = lambda / sum(lambda);
% 计算累计贡献率
cumulativeRate = cumsum(contributionRate);
% 计算行轮廓坐标
beta = diag(rowRatio.^(-1 / 2)) * U_adjusted;
G = beta * S
% 计算列轮廓坐标
alpha = diag(columnRatio.^(-1 / 2)) * V_adjusted;
F = alpha * S
% 计算样本点的个数
numOfSample = size(G, 1);
% 计算坐标的取值范围
range = minmax(G(:, [1, 2])');
% 画图略
4.结果
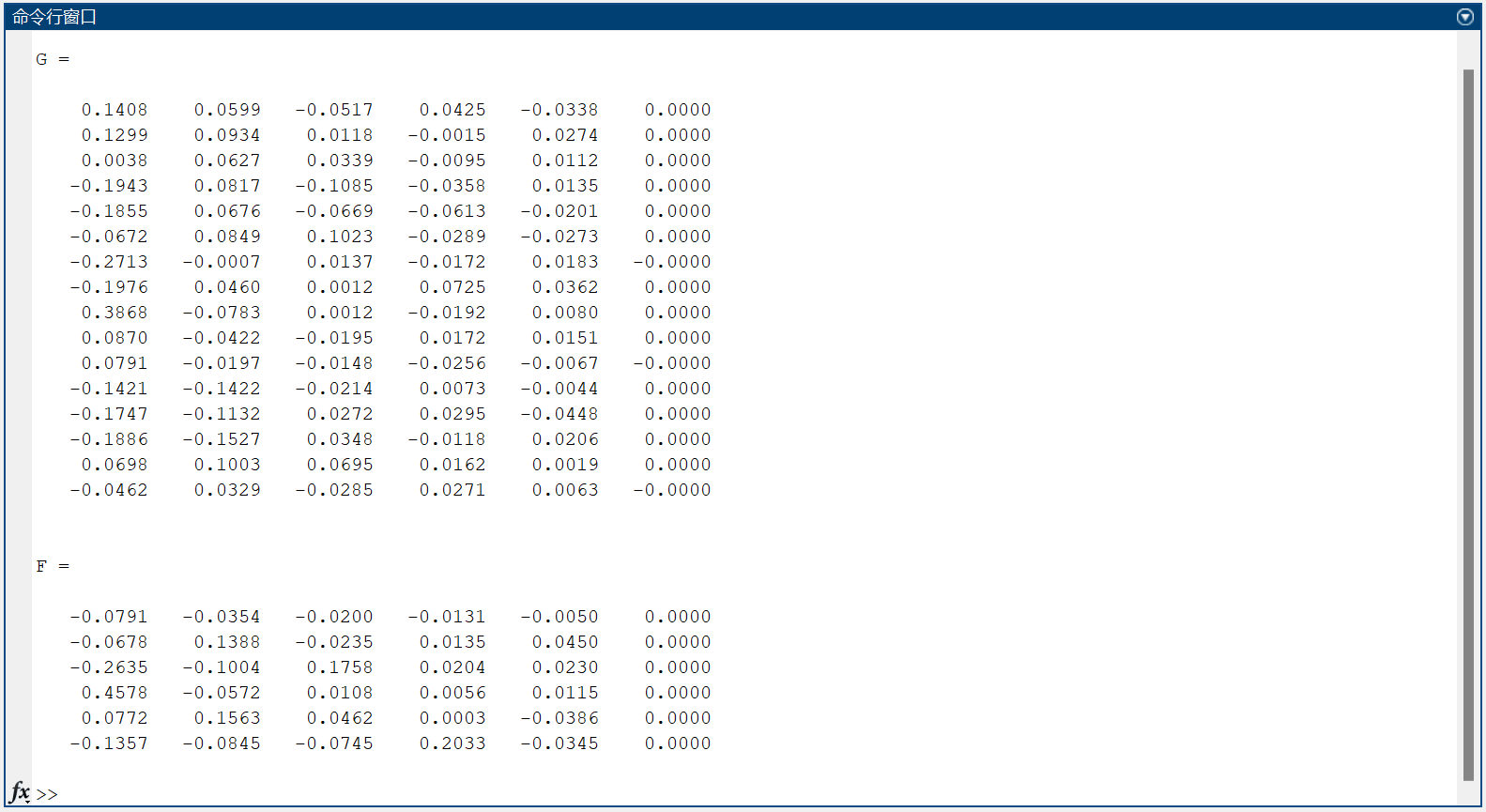
详见上文分析过程,地区和指标点可以分为两类,
第一类包括指标点 x 4 , x 5 x_4,x_5 x4?,x5? ,地区点为北京、天津、河北、上海、江苏、浙江、山东;
第二类包括指标点 x 1 , x 2 , x 3 , x 6 x_1,x_2,x_3,x_6 x1?,x2?,x3?,x6? ,地区点为其余地区。
习题10.6(2)
1. 题目要求
同上。
2.解题过程——R型因子分析
解:
对数据进行标准化处理。
计算变量间的相关系数得出相关矩阵 R \mathbf{R} R ,然后计算初等载荷矩阵 Λ 1 \mathbf{\Lambda_1} Λ1? 。
计算得到特征根与各因子的贡献如下表所示。
| value | x1 | x2 | x3 | x4 | x5 | x6 |
|---|---|---|---|---|---|---|
| 特征值 | 3.55842 | 1.316252 | 0.608239 | 0.373383 | 0.107178 | 0.036527 |
| 贡献率 | 59.30701 | 21.93754 | 10.13732 | 6.223052 | 1.786295 | 0.608786 |
| 累积贡献率 | 59.30701 | 81.24454 | 91.38187 | 97.60492 | 99.39121 | 100 |
选择
m
(
m
≤
6
)
m(m\leq6)
m(m≤6) 个主因子,构造因子模型:
{
x
~
1
=
α
11
F
~
1
+
α
12
F
~
2
+
α
13
F
~
3
?
x
~
7
=
α
71
F
~
1
+
α
72
F
~
2
+
α
73
F
~
3
\begin{align*} \begin{cases} \widetilde{x}_1=\alpha_{11}\widetilde{F}_1+\alpha_{12}\widetilde{F}_2+\alpha_{13}\widetilde{F}_3 \\ \vdots\\ \widetilde{x}_7=\alpha_{71}\widetilde{F}_1+\alpha_{72}\widetilde{F}_2+\alpha_{73}\widetilde{F}_3 \end{cases}\end{align*}
?
?
??x
1?=α11?F
1?+α12?F
2?+α13?F
3??x
7?=α71?F
1?+α72?F
2?+α73?F
3???
求得因子载荷等估计。
最终,通过表格,可以看出,得到了3个因子,第一个因子是穿住用因子,第二个因子是燃料因子,第3个因子是文化因子。
第(1)问中得到 x 4 , x 5 x_4,x_5 x4?,x5? 是一类变量,这里得到 x 2 , x 4 , x 5 x_2,x_4,x_5 x2?,x4?,x5? 是一类变量,略有差异。
3.程序
求解的MATLAB程序如下:
clc, clear
% 原始数据,包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
101.18, 23.26, 8.46, 20.20, 20.50, 4.30];
% 数据标准化
standardizedData = zscore(originalData);
% 计算相关性矩阵
correlationMatrix = corrcoef(standardizedData);
% 使用主成分分析方法对相关性矩阵进行处理,得到特征向量、特征值和贡献率
[eigenvectors, eigenvalues, contribution] = pcacov(correlationMatrix);
% 计算累积贡献率
cumulativeContribution = cumsum(contribution);
% 根据特征向量的符号进行调整
adjustedSigns = repmat(sign(sum(eigenvectors)), size(eigenvectors, 1), 1);
adjustedEigenvectors = eigenvectors .* adjustedSigns;
% 根据特征值进行缩放
scaledFactors = repmat(sqrt(eigenvalues)', size(adjustedEigenvectors, 1), 1);
scaledEigenvectors = adjustedEigenvectors .* scaledFactors;
% 计算贡献率
contribution1 = sum(scaledEigenvectors.^2);
% 选择的因子数量
factorNum = 3;
% 根据选择的因子数量得到对应的因子
selectedFactors = scaledEigenvectors(:, [1:factorNum]);
% 使用方差最大法进行因子旋转
[rotatedFactors, factorMatrix] = rotatefactors(selectedFactors, 'method', 'varimax')
% 合并旋转后的因子和其他因子
mergedFactors = [rotatedFactors, scaledEigenvectors(:, [factorNum + 1:end])];
% 计算因子载荷量
factorLoads = sum(rotatedFactors.^2, 2)
% 计算贡献率
contribution2 = sum(mergedFactors.^2)
% 计算每个因子的贡献率
contributionRate = contribution2(1:factorNum) / sum(contribution2);
% 计算因子得分系数矩阵
factorScoreCoefficients = inv(correlationMatrix) * rotatedFactors;
4.结果
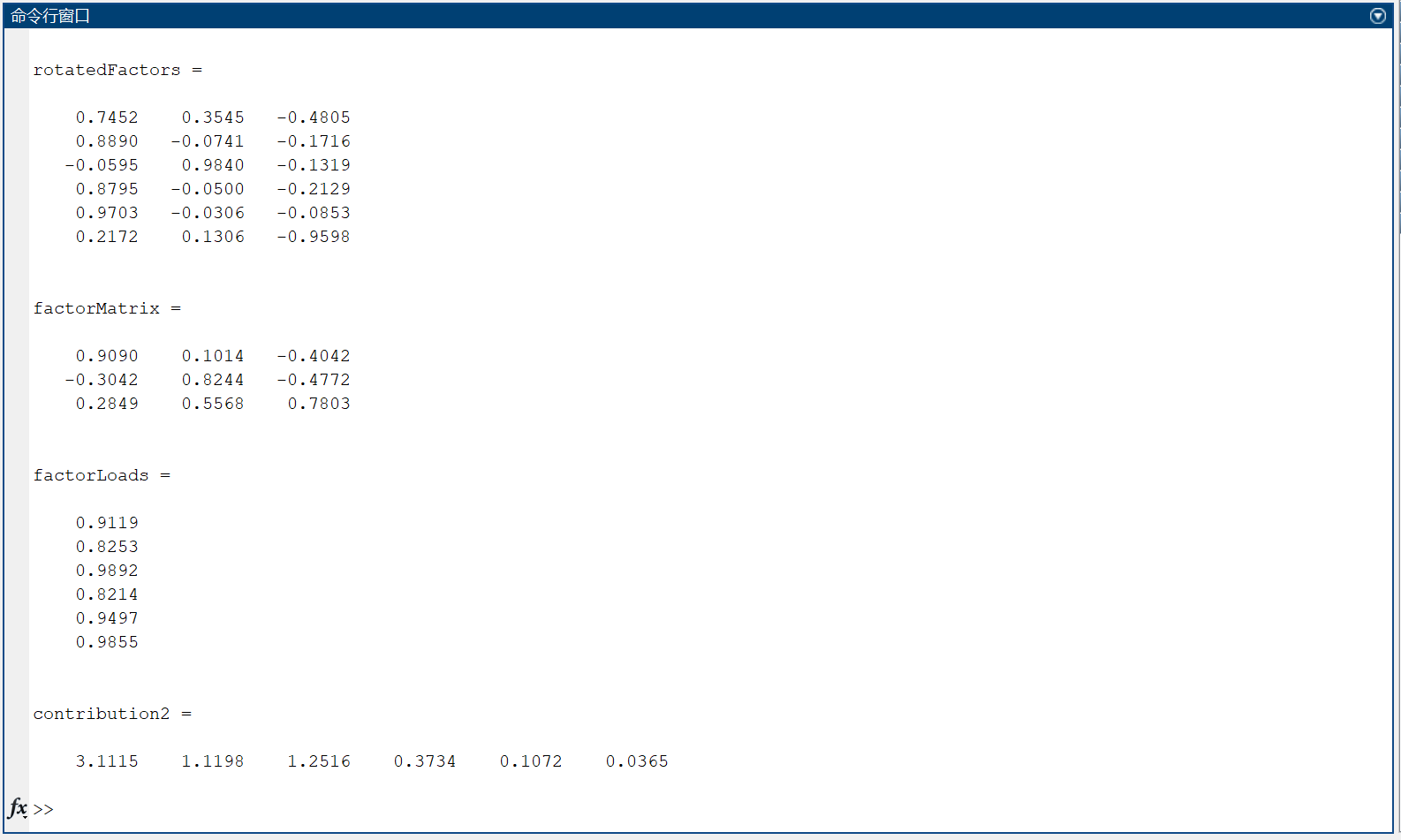
求得因子载荷等估计如下表所示。

可以看出,得到了3个因子,第一个因子是穿住用因子,第二个因子是燃料因子,第3个因子是文化因子。
第(1)问中得到 x 4 , x 5 x_4,x_5 x4?,x5? 是一类变量,这里得到 x 2 , x 4 , x 5 x_2,x_4,x_5 x2?,x4?,x5? 是一类变量,略有差异。
习题10.6(3)
1. 题目要求
同上。
2.解题过程——聚类分析
解:
首先计算变量间的相关系数。用两变量
x
j
x_j
xj?与
x
k
x_k
xk?的相关系数作为它们的相似性度量,即
x
j
x_j
xj?与
x
k
x_k
xk?的相似系数为
r
j
k
=
∑
i
=
1
16
(
a
i
j
?
μ
j
)
(
a
i
k
?
μ
k
)
[
∑
i
=
1
16
(
a
i
j
?
μ
j
)
2
∑
i
=
1
16
(
a
i
k
?
μ
k
)
2
]
1
/
2
,
j
,
k
=
1
,
…
,
6.
r_{jk} = \frac{\sum_{i=1}^{16}(a_{ij}-\mu_{j})(a_{ik}-\mu_k)} {[\sum_{i=1}^{16}(a_{ij}-\mu_{j})^2\sum_{i=1}^{16}(a_{ik}-\mu_k)^2]^{1/2}},j,k=1,\dots,6.
rjk?=[∑i=116?(aij??μj?)2∑i=116?(aik??μk?)2]1/2∑i=116?(aij??μj?)(aik??μk?)?,j,k=1,…,6.
然后计算6个变量两两之间的距离,构造距离矩阵。
接着使用最短距离法来测量类与类之间的距离,记类
G
p
G_{p}
Gp?和
G
q
G_{q}
Gq?之间的距离:
D
(
G
p
,
G
q
)
=
min
?
i
∈
G
p
,
k
∈
G
q
d
i
k
.
D(G_p,G_q) = \min_{i\in G_p,k\in G_q }{d_{ik}}.
D(Gp?,Gq?)=i∈Gp?,k∈Gq?min?dik?.
变量聚类的结果是变量
x
3
x_3
x3?自成一类,其他变量为一类。画出的变量聚类图如下图所示。
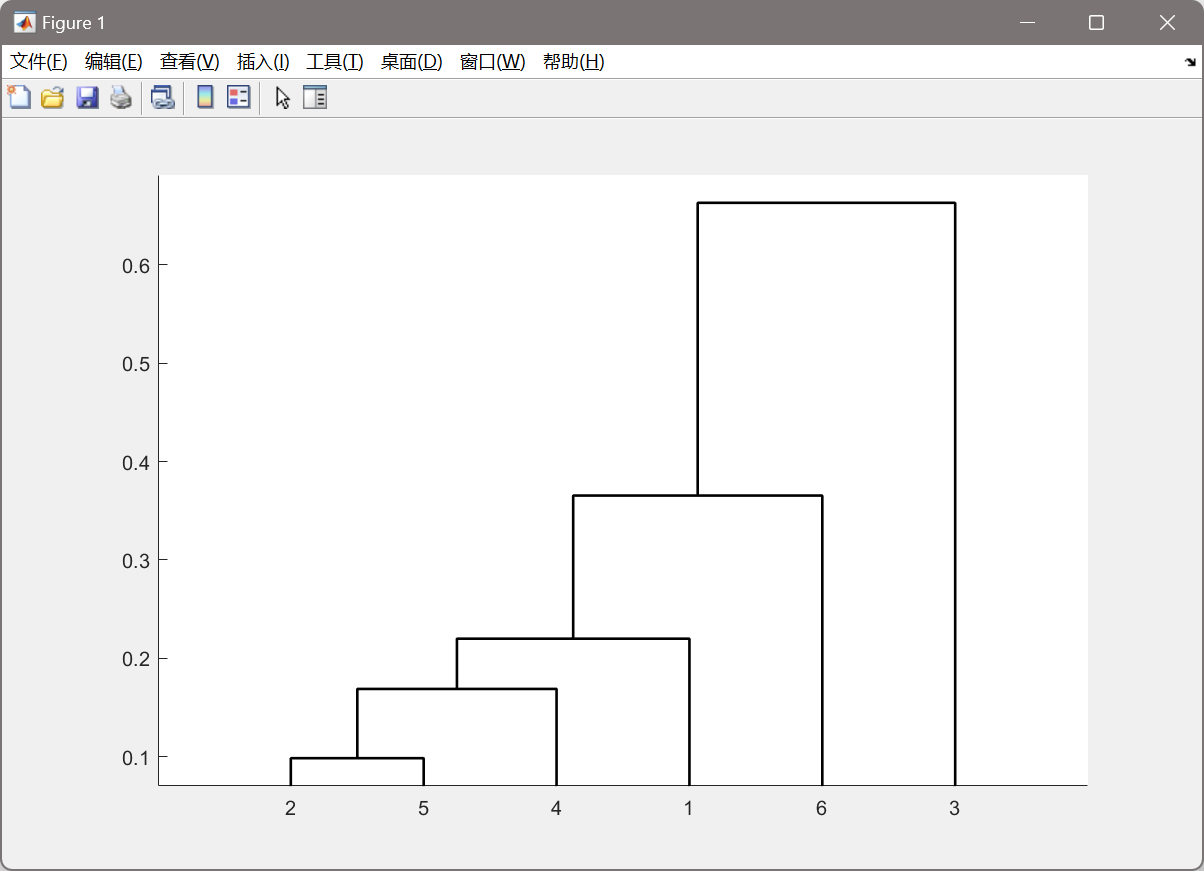
最后进行样本点聚类的 Q \mathbf{Q} Q型聚类分析。
计算16个样本点之间的两两马氏距离。
类与类间相似性度量。
画聚类图,并对样本点进行分类。
样本点的聚类结果如下图所示。通过聚类图,可以把地区分成4类,北京自成一类,吉林自成一类,上海自成一类,其他地区为一类。

3.程序
求解的MATLAB程序如下:R型聚类
clc, clear
% 原始数据,包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
101.18, 23.26, 8.46, 20.20, 20.50, 4.30];
% 计算相关性矩阵
correlationMatrix = corrcoef(originalData);
% 计算距离矩阵
distanceMatrix = 1 - abs(correlationMatrix);
distanceMatrix = tril(distanceMatrix);
% 将距离矩阵转为一维向量
distanceVector = nonzeros(distanceMatrix);
distanceVector = distanceVector';
% 使用层次聚类算法进行聚类
linkageCluster = linkage(distanceVector);
% 选择最大聚类数量为2,得到每个样本的类别
clusterLabels = cluster(linkageCluster, 'maxclust', 2);
% 找到属于第一类的样本
index1 = find(clusterLabels == 1);
index1 = index1'
% 找到属于第二类的样本
index2 = find(clusterLabels == 2);
index2 = index2'
% 生成树状图
h = dendrogram(linkageCluster);
% 设置树状图的颜色和线条宽度
set(h, 'Color', 'k', 'LineWidth', 1.3)
求解的MATLAB程序如下:Q型聚类
clc, clear
% 原始数据,包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
101.18, 23.26, 8.46, 20.20, 20.50, 4.30];
% 计算原始数据的协方差
covarianceMatrix = cov(originalData);
% 初始化距离矩阵
distanceMatrix = zeros(size(originalData, 1));
% 计算Q型距离
for j = 1:15
for i = j+1:16
distanceMatrix(i,j) = sqrt((originalData(i,:) - originalData(j,:)) * inv(covarianceMatrix) * (originalData(i,:) - originalData(j,:))');
end
end
% 将距离矩阵转为一维向量
distanceVector = nonzeros(distanceMatrix);
distanceVector = distanceVector';
% 使用层次聚类算法进行聚类
linkageCluster = linkage(distanceVector);
% 生成树状图
dendro = dendrogram(linkageCluster);
% 设置树状图的颜色和线条宽度
set(dendro,'Color','k','LineWidth',1.3)
4.结果

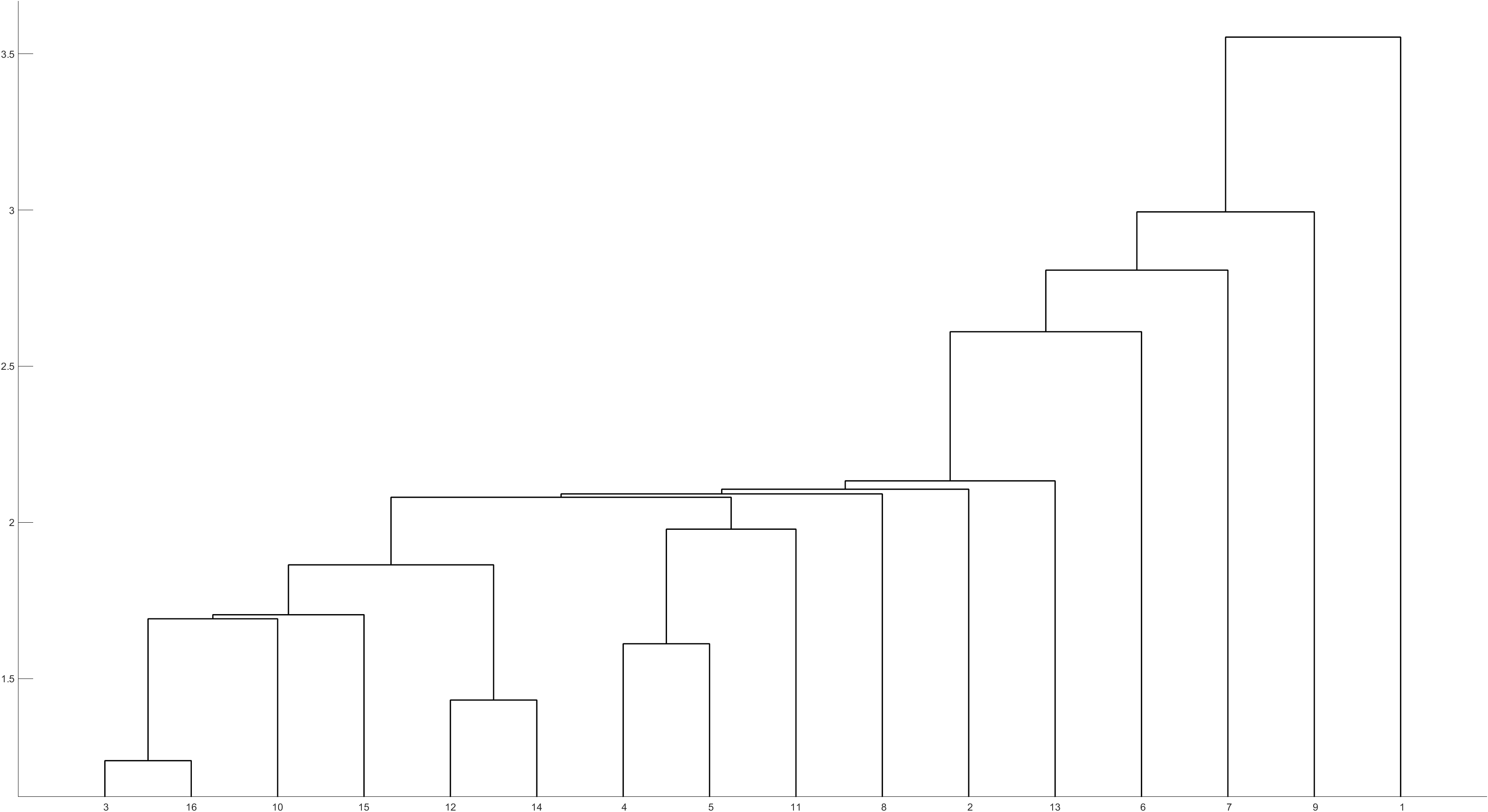
变量 x 3 x_3 x3?自成一类,其他变量为一类。
北京自成一类,吉林自成一类,上海自成一类,其他地区为一类。
如果这篇文章对你有帮助,欢迎点赞与收藏~
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- SpringBoot整合Dubbo常用注解类说明
- Spring Boot核心特性、注解和Bean作用域
- linux网络管理_配置网络参数
- Filter Options in Select Field
- Hackathon | Mint Blockchain 启动全球 NIP 创意提案黑客松活动!
- MySQL视图特性
- CTFhub-网站源码
- IEEE Trans模板参考文献中若相同作者的两篇文章放一起第二篇作者姓名不显示
- 电力能源实景三维可视化合集,智慧电网数字孪生
- 为什么Controller就报错404,而改为RestController就不报错了