二分查找(一)
算法原理?
原理:当一个序列有“二段性”的时候,就可以使用二分查找算法。
适用范围:根据规律找一个点,能将这个数组分成两部分,根据规律能有选择性的舍去一部分,进而在另一个部分继续查找。
除了最普通的二分查找,剩余的二分查找都是以 left == right 为结束条件。
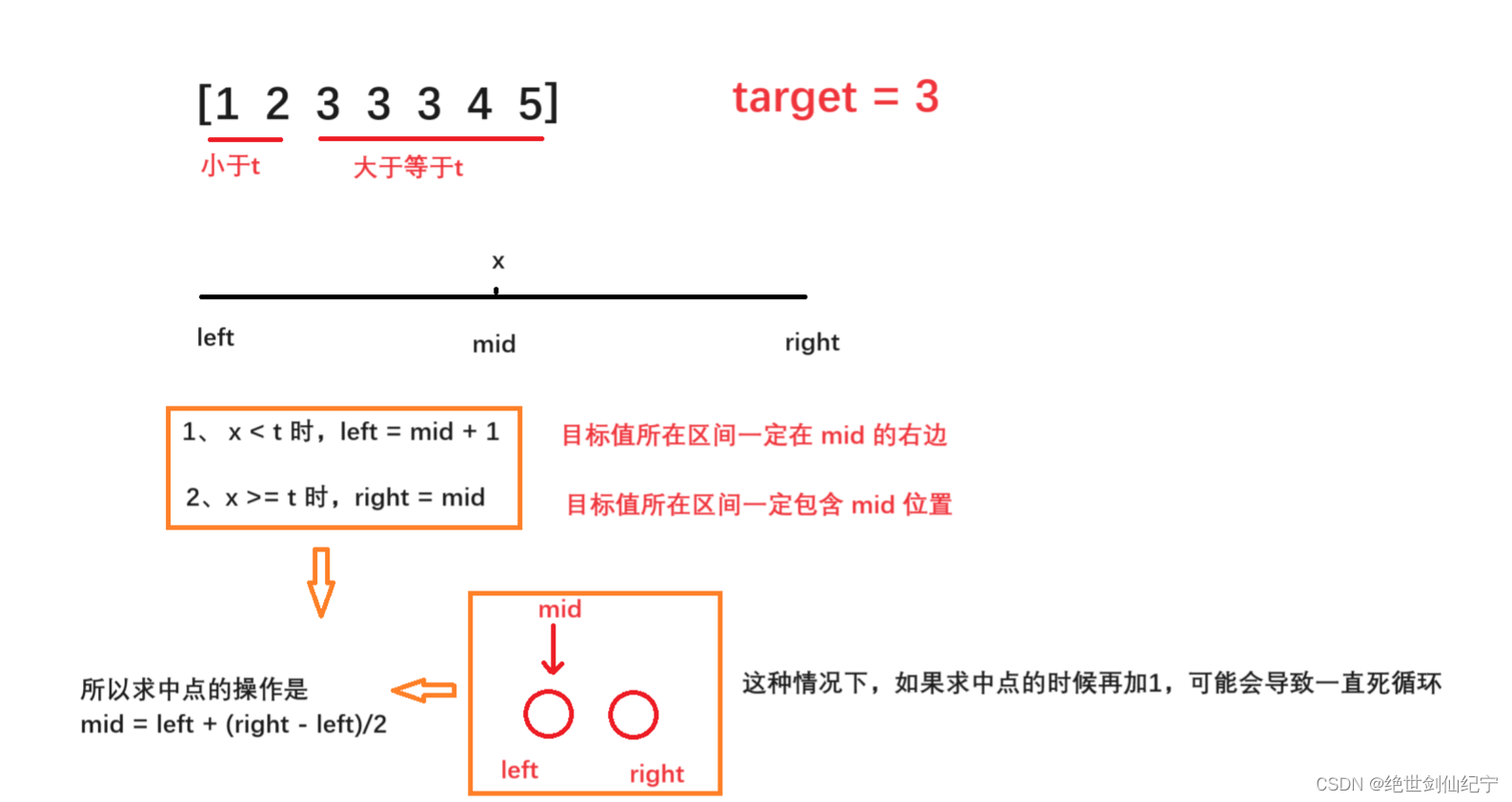
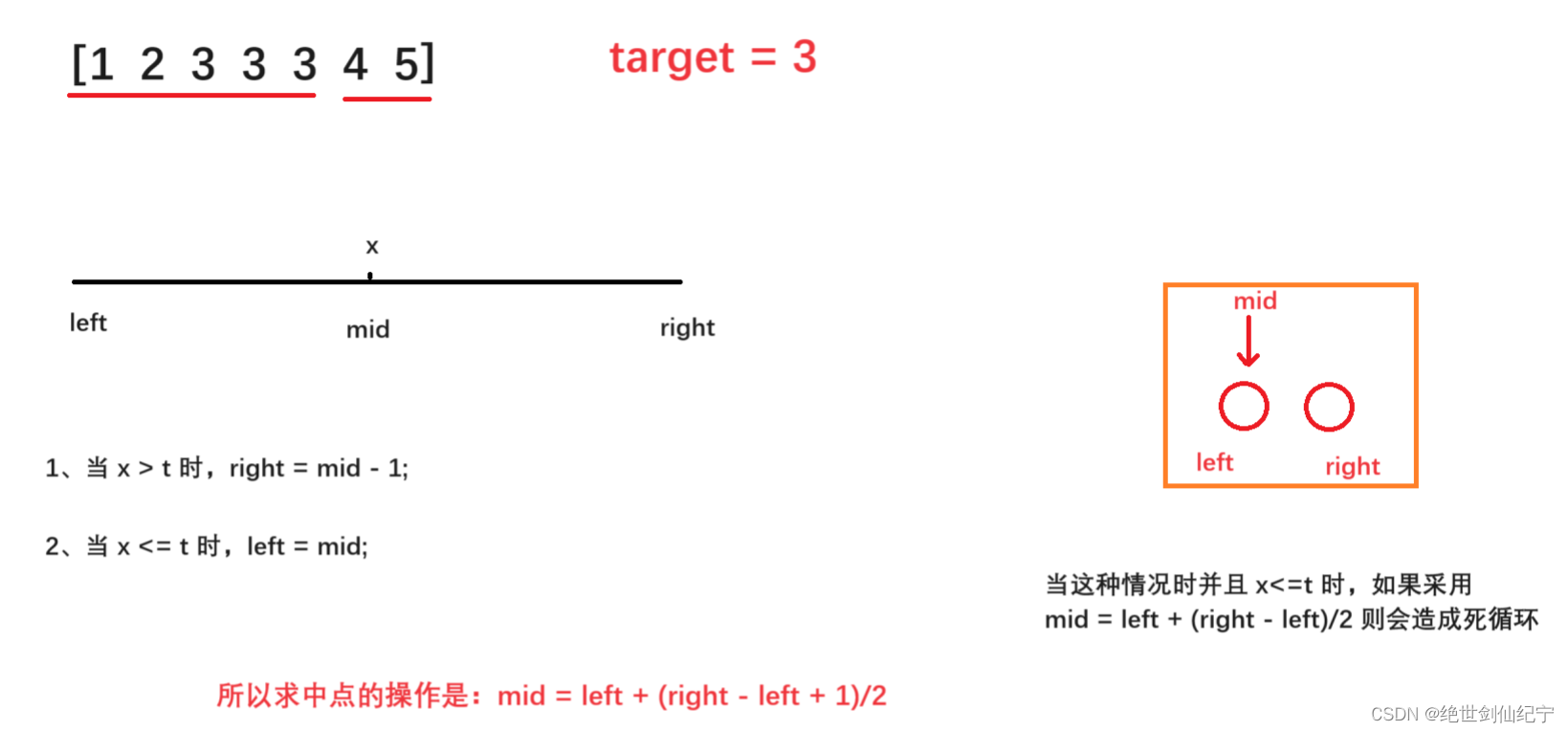
找中点 mid方法:left+(right - left)/2(查找区间左端点的情况);left+(right-left+1)/2(查找区间右端点的情况)
循环判断结束方法:left<=right(普通二分查找)?left<right(查找左边界或有边界的二分情况)
下图是找左边界的思路:将区间分为小于目标值和大于等于目标值两部分
同理,当找右区间的时候:
如何区分这些模板呢?
先将所求区间分为两个子区间,目标下标一定要为这两个子区间的区间边界处,当求左区间的端点的时候,求中点的操作是 mid = left + (right - left)/2 ,这种求中点的方式,当区间总元素数为偶数的时候,恰好求的是靠左边的那一个中间的数,而 mid = left + (right - left +1)/2 则求出的是靠右边的那一个中间的数。
将区分这两个区间的条件,作为每次二分舍去一部分的依仗,舍去不存在目标值的那部分(... = mid + 1 或 ... = mid - 1);靠近目标值(... = mid)
二分查找
给定一个?n?个元素有序的(升序)整型数组?nums?和一个目标值?target??,写一个函数搜索?nums?中的?target,如果目标值存在返回下标,否则返回?-1。

此题为一道普通二分题目,很简单
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while(left<=right)
{
int mid = (left + right)/2;
if(nums[mid]==target) return mid;
else if(nums[mid]<target) left = mid + 1;
else right = mid - 1;
}
return -1;
}
};在排序数组中查找元素的第一个和最后一个位置?
???????在排序数组中查找元素的第一个和最后一个位置??????
 ?
?
此题是查找左端点与查找右端点结合的题目,只需再处理一下特殊情况即可。
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.size()==0) return {-1,-1};
// 1. 找左端点
int left = 0, right = nums.size() - 1, mid = 0;
vector<int> v1;
while(left < right)
{
mid = left + (right - left) /2;
if(nums[mid] < target) left = mid + 1;
if(nums[mid] >= target) right = mid;
}
if(nums[left]!=target) return {-1,-1};
v1.push_back(left);
// 2. 找右端点
left = 0, right = nums.size() - 1;
while(left < right)
{
mid = left + (right - left + 1) /2;
if(nums[mid] <= target) left = mid;
if(nums[mid] > target) right = mid -1;
}
v1.push_back(left);
return v1;
}
};x 的平方根?
给你一个非负整数?x?,计算并返回?x?的?算术平方根?。
由于返回类型是整数,结果只保留?整数部分?,小数部分将被?舍去 。
注意:不允许使用任何内置指数函数和算符,例如?pow(x, 0.5)?或者?x ** 0.5?。
?
转化为求区间的右端点的二分问题
class Solution {
public:
int mySqrt(int x) {
if(x == 0) return 0;
long long left = 1, right = x;
while(left < right)
{
long long mid = (left + right + 1) /2;
if(mid * mid <= x) left = mid;
if(mid * mid > x) right = mid -1;
}
return left;
}
};搜索插入位置?
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为?O(log n)?的算法。

转化为找区间左端点的问题。其实也可以转化为找区间右端点的问题,但需要处理的细节更多!
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while(left < right)
{
int mid = left + (right - left )/2;
if(nums[mid] < target) left = mid + 1;
else right = mid;
}
if(nums[left] < target) return left + 1;
else return left;
}
};本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 批量给Linux服务器推送文件、执行指令的工具推荐 - wgcloud-bach-agent
- 第三章、远程连接服务器
- 外包干了3个月,技术退步明显
- PythonStudio:一款国人写的python及窗口开发编辑IDE,可以替代pyqt designer等设计器了
- 基于DBNetpp的文本检测的仪表盘读数识别
- 第84讲:基于各种场景使用mysqldump逻辑备份数据库
- 求范围内回文素数
- 如何学习程序设计?
- 循环依赖和三级缓存
- springboot+mysql大学生兼职网站-计算机毕业设计源码08011