NLP深入学习（八）：感知机学习

---

0. 引言

前情提要：
《NLP深入学习（一）：jieba 工具包介绍》
《NLP深入学习（二）：nltk 工具包介绍》
《NLP深入学习（三）：TF-IDF 详解以及文本分类/聚类用法》
《NLP深入学习（四）：贝叶斯算法详解及分类/拼写检查用法》
《NLP深入学习（五）：HMM 详解及字母识别/天气预测用法》
《NLP深入学习（六）：n-gram 语言模型》
《NLP深入学习（七）：词向量》

1. 感知机

感知机（Perceptron）是一种基于线性模型的监督学习算法，主要用于解决二分类问题。它是神经网络和许多其他机器学习算法的基础模型之一，由弗兰克·罗森布拉特（Frank Rosenblatt）于1957年提出。

1.1 基本概念与结构

• 感知机模型试图找到一个超平面来分割特征空间中的数据点，使得不同类别的样本分别位于超平面的两侧。
• 超平面可以用线性函数表示：
  $$f(x)=w^{T}x+b$$
  其中 $x$ 是输入特征向量，$w$ 是权值向量（weight vector），$b$ 是偏置项（bias），$sign(f(x))$ 表示对输入 $x$ 的分类结果，通常取+1或-1。
  

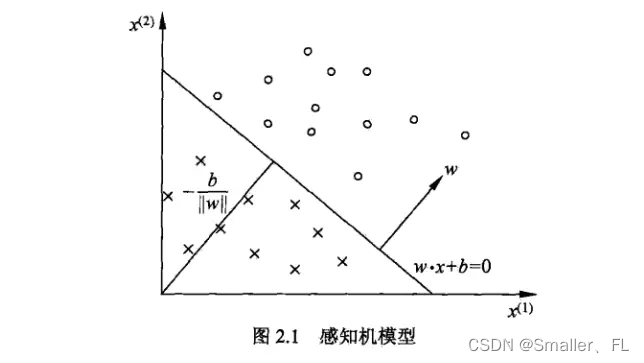
1.2 学习策略

感知机的学习策略：确定参数$w$和$b$，定义一个损失函数并将其最小化。损失函数一般是选择误分类点到超平面的距离和：
$$\frac{|w?x+b|}{||w||}$$
$||w||$是 $w$ 的第二范数。因为$y$取值是+1和-1，对于误分类的点有：
$$?y_i(w?x+b)>0$$
因此，误分类点 $x_i$ 到超平面的距离是：
$$?\frac{1}{||w||}{y}_i(w?x+b)$$
那么所有的误分类点到超平面的总和距离为：
$$?\frac{1}{||w||}\sum _{x_i\in M}{y}_i(w?x_i+b)$$
不必考虑 $\frac{1}{||w||}$，则得到感知机的损失函数：
$$L(w,b)=?\sum _{x_i\in M}{y}_i(w?x_i+b)$$
其中M为误分类的点的集合。

2. 感知机学习算法

2.1 原始形式

已经确定了感知机的损失函数，那么其原始形式只需要最小化这个损失函数：
$$\underset{w,b}{\min }L(w,b)=?\sum _{x_i\in M}{y}_i(w?x_i+b)$$

随机梯度下降法初始时任选 $w_0$，$b_0$作为初始超平面，如果有误分类点，随机选取一个误分类点，进行梯度下降，计算损失函数的梯度：
$$\begin{array}{rl}{▽}_{w}L(w,b)& =?\sum _{x_i\in M}{y}_i{x}_i\\ {▽}_{w}L(w,b)& =?\sum _{x_i\in M}{y}_i\end{array}$$
梯度下降法使参数向反方向变化，使用随机选出的误分类点的数据，根据提前设置好的学习率对进行更新：
$$\begin{array}{rl}w& \leftarrow w+\eta y_i{x}_i\\ b& \leftarrow b+\eta y_i\end{array}$$
使损失函数不断减小，直到为0时就得到了可正确分类数据集的超平面。

2.2 对偶形式

感知机（Perceptron）的对偶形式是针对原始形式进行优化的一种方法，其基本思想是将原问题转换为对偶形式，从而改变算法求解的方式。在解决线性可分数据集的二分类问题时，原始的感知机算法通过迭代更新权重向量 $w$ 来找到一个能够正确划分正负样本的超平面。

对偶形式则引入了拉格朗日乘子法，并且使用了一种基于误分类点的表示方式。在这个形式下，不再直接更新权重向量 $w$，而是维护一组系数 $\alpha$，每个系数对应训练集中的一条误分类样例。对偶形式的核心更新规则是在每次迭代中调整这些系数 $\alpha$，而不是权值向量和偏置项。

可将每次 $w,b$ 增量表示为 ${\alpha }_i{y}_i{x}_i,{\alpha }_i{y}_i$，其中 $\alpha =n_i\eta$，假设$w_0=b_0=0$（无关要紧），更新过程表示为：
$$\begin{array}{rl}w& =\sum _i{\alpha }_i{y}_i{x}_i\\ b& =\sum _i{\alpha }_i{y}_i\end{array}$$

感知机模型可由$\alpha ,b$表出。
$$f(x)=sign(\sum _j{\alpha }_j{y}_j?x+b)$$

在判断是否是误分类点时用
$$y_i(\sum _j{\alpha }_j{y}_j{x}_j?x_i+b)?0$$
更新时
$$\begin{array}{rl}{\alpha }_i& \leftarrow {\alpha }_i+\eta \\ b& \leftarrow b+\eta y_i\end{array}$$

对偶形式的优势在于它可能比原始形式收敛更快，尤其是在大规模稀疏数据集上，因为它的计算主要集中在误分类样本上。另外，对偶形式对于支持向量机（SVM）的学习算法也有重要影响，SVM 的对偶形式也是通过类似的拉格朗日对偶变换得到的，并且在实际应用中有更优的表现。

3. 参考

《NLP深入学习（一）：jieba 工具包介绍》
《NLP深入学习（二）：nltk 工具包介绍》
《NLP深入学习（三）：TF-IDF 详解以及文本分类/聚类用法》
《NLP深入学习（四）：贝叶斯算法详解及分类/拼写检查用法》
《NLP深入学习（五）：HMM 详解及字母识别/天气预测用法》
《NLP深入学习（六）：n-gram 语言模型》
《NLP深入学习（七）：词向量》