2024年华数杯国际赛A题:放射性废水处理建模 思路模型代码解析
2024年华数杯国际赛A题:放射性废水处理建模(Radioactive Wastewater from Japan)
一、问题描述
2011年3月,日本东海岸发生了地震,引发了福岛第一核电站事故,导致三个核反应堆熔毁,并在一场巨大海啸中冲毁了电站的冷却系统,核燃料产生融化的碎片。为了冷却熔化的核燃料,海水不断注入反应堆,导致大量放射性核素污染的冷却水。尽管全球各国人民反对,日本政府于2023年8月24日开始强制排放经过处理的福岛放射性废水到太平洋。受核素污染的放射性废水总量超过100万吨。整个项目预计将至少持续30年。附录是日本政府公布的四轮排放计划。

这些核废水含有氚,一种可以在环境中存在很长时间的放射性同位素。放射性元素的污染程度是指环境中存在的放射性元素的数量以及对人类和生态系统的潜在危害程度。通常通过测量放射性元素的浓度、辐射水平、半衰期等参数来评估。氚的高放射性使其具有通过辐射损害细胞和组织的潜力。在海洋环境中,氚将被生物吸收并进入食物链,导致对生态系统中的物种造成辐射损害,影响海洋生物的繁殖和生态平衡。
放射性废水在海水中的扩散路径受到许多因素的影响,包括水流、海床地形、水深、潮汐和季节变化以及环境条件。了解放射性废水在环境中的传输和扩散可以帮助我们评估对周围海洋生态系统和人类健康的巨大影响。
通过建立数学模型和分析,我们可以预测核废水的扩散范围和路径,制定环境保护措施和应急计划。
- 建立扩散数学模型,描述海水中放射性废水扩散的速率和方向,考虑水流、环境条件和其他影响因素。已知截至2023年8月27日上午12:00,从日本排放的放射性废水量为1095吨。如果不再排放放射性废水,请预测到2023年9月27日时在日本附近海域的放射性废水污染范围和程度。
- 在2023年,日本政府已经三次排放了放射性废水。如果将来不再排放,请建立数学模型研究三次排放后放射性废水的扩散路径。考虑海洋环流模式、水流动力学、海床地形、水深变化、潮汐影响和季节波动等因素。估计污染中国领海需要多长时间。
- 在日本政府宣布排放放射性废水后,相关部门对1万名中国居民进行了调查。调查包括他们在废水排放前后是否购买和食用海鲜。表1显示了调查结果。根据表1中给出的调查结果,分析放射性废水排放对中国未来渔业经济的长期影响。表1:关于放射性废水排放事件后是否购买和食用海鲜的调查结果。注意:现在吃海鲜和现在不吃海鲜指的是废水排放进海后的态度。
- 在日本排放放射性废水30年后,请判断世界所有海域是否都会受到污染。哪一年将完全污染?其中哪个地方将受到最严重污染?
- 根据你的研究,写一封一页的建议信给联合国环境计划。
附录:
- 每轮结束时间:2023年9月9日,2023年10月23日,2023年11月20日,2024年2月
- 排放的核污染水重量:7100吨,7810吨,7753吨,约7800吨
二、解题思路
问题一思路
【更多思路扫描文章下方二维码获取~~】
问题一要求建立一个数学模型来描述海水中放射性废水的扩散情况。这个问题不能简单的套用机器学习模型,应该使用机理分析的方法来进行建模。我们可以考虑使用扩散方程(Diffusion Equation)来描述放射性物质在水体中的传播,扩散方程可以采用一维或二维的形式,取决于具体情况。
下面给出一维扩散模型的简单示例:
(1)一维扩散模型
1、扩散方程
一维扩散方程可以表示为:
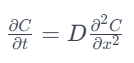
其中:
- C 是废水的浓度(单位:质量/体积),
- t 是时间,
- x 是空间坐标,
- D 是扩散系数。
2、初始和边界条件:
初始条件: 初始时刻的浓度分布。
![]()
边界条件: 在空间边界的浓度。
![]()
这里,L 是空间的长度。
3、数值求解方法:
扩散方程的数值解可以通过有限差分法等方法进行离散化求解。通过将时间和空间分割成离散的步长,可以使用迭代方法来模拟废水的扩散过程。
import numpy as np
import matplotlib.pyplot as plt
# 模型参数
D = 0.01 # 扩散系数
L = 100 # 空间长度
T = 30 # 模拟的总时间
Nx = 100 # 空间网格数
Nt = 300 # 时间步数
# 空间和时间步长
dx = L / Nx
dt = T / Nt
# 初始化浓度场
C = np.zeros((Nx, Nt+1))
# 设置初始条件
C[:, 0] = 0.0 # 初始浓度为零
# 数值求解
for t in range(Nt):
for x in range(1, Nx-1):
C[x, t+1] = C[x, t] + D * dt / dx**2 * (C[x+1, t] - 2*C[x, t] + C[x-1, t])
# 绘制结果
plt.imshow(C, extent=[0, T, 0, L], aspect='auto', cmap='viridis')
plt.colorbar(label='浓度')
plt.xlabel('时间')
plt.ylabel('空间位置')
plt.title('放射性废水扩散模拟')
plt.show()
(2)二维扩散模型
1、扩散方程
二维扩散方程可以表示为:

其中:
- C 是废水的浓度,
- t 是时间,
- x 和 y 是空间坐标,
- D 是扩散系数。
2、初始和边界条件
初始条件:初始时刻的浓度分布。
边界条件:在空间边界的浓度。
3、数值求解方法
使用有限差分法或其他数值方法对二维扩散方程进行离散化求解。将空间和时间分割成离散的步长,通过迭代模拟废水在二维空间中的扩散过程。
import numpy as np
import matplotlib.pyplot as plt
# 模型参数
D = 0.01 # 扩散系数
Lx = Ly = 100 # 空间长度
T = 30 # 模拟的总时间
Nx = Ny = 100 # 空间网格数
Nt = 300 # 时间步数
# 空间和时间步长
dx = Lx / Nx
dy = Ly / Ny
dt = T / Nt
# 初始化浓度场
C = np.zeros((Nx, Ny, Nt+1))
# 设置初始条件
C[:, :, 0] = 0.0 # 初始浓度为零
# 数值求解
for t in range(Nt):
for x in range(1, Nx-1):
for y in range(1, Ny-1):
C[x, y, t+1] = C[x, y, t] + D * dt / dx**2 * (C[x+1, y, t] - 2*C[x, y, t] + C[x-1, y, t]) + D * dt / dy**2 * (C[x, y+1, t] - 2*C[x, y, t] + C[x, y-1, t])
# 绘制结果
plt.imshow(C[:, :, Nt], extent=[0, Lx, 0, Ly], aspect='auto', cmap='viridis')
plt.colorbar(label='浓度')
plt.xlabel('空间位置 (x)')
plt.ylabel('空间位置 (y)')
plt.title('放射性废水二维扩散模拟')
plt.show()
问题二思路
【更多思路扫描文章下方二维码获取~~】
问题二涉及到建立数学模型来研究三次排放后放射性废水在海水中的扩散路径,考虑了海洋环流模式、水流动力学、海床地形、水深变化、潮汐影响和季节波动等因素。
以下是详细解题思路步骤:
- 模型选择: 选择适当的三维扩散模型,考虑海洋环流模式等因素。
- 模型参数: 确定模型中的参数,如扩散系数、海洋流速、潮汐周期等。
- 初始和边界条件: 设置初始时刻的浓度分布和边界条件,反映排放时的初始状态。
- 数值求解: 使用数值方法,如有限元法或有限差分法,对三维扩散模型进行离散化求解。
- 路径追踪: 根据数值解,追踪废水在海水中的扩散路径,考虑流体运动和地形等因素。
数学模型:三维扩散模型
1、扩散方程
三维扩散方程可以表示为:
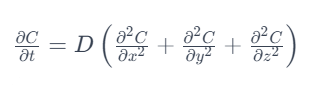
其中:
- C 是废水的浓度,
- t 是时间,
- x, y 和 z 是空间坐标,
- D 是扩散系数。
2、初始和边界条件
初始条件:初始时刻的浓度分布。
边界条件:在空间边界的浓度。
3、数值求解方法
使用有限差分法或其他数值方法对三维扩散方程进行离散化求解。将空间和时间分割成离散的步长,通过迭代模拟废水在三维空间中的扩散过程。下面代码是使用有限差分法求解三维扩散模型,并追踪废水扩散路径的示例代码:
import numpy as np
import matplotlib.pyplot as plt
# 模型参数
D = 0.01 # 扩散系数
L = 100 # 空间长度
T = 30 # 模拟的总时间
Nx = Ny = Nz = 100 # 空间网格数
Nt = 300 # 时间步数
# 空间和时间步长
dx = dy = dz = L / Nx
dt = T / Nt
# 初始化浓度场
C = np.zeros((Nx, Ny, Nz, Nt+1))
# 设置初始条件
C[:, :, :, 0] = 0.0 # 初始浓度为零
# 数值求解
for t in range(Nt):
for x in range(1, Nx-1):
for y in range(1, Ny-1):
for z in range(1, Nz-1):
C[x, y, z, t+1] = C[x, y, z, t] + D * dt / dx**2 * (C[x+1, y, z, t] - 2*C[x, y, z, t] + C[x-1, y, z, t]) + \
D * dt / dy**2 * (C[x, y+1, z, t] - 2*C[x, y, z, t] + C[x, y-1, z, t]) + \
D * dt / dz**2 * (C[x, y, z+1, t] - 2*C[x, y, z, t] + C[x, y, z-1, t])
# 绘制结果(路径追踪)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(xs=path_x, ys=path_y, zs=path_z, c='r', marker='o', label='Path')
ax.set_xlabel('空间位置 (x)')
ax.set_ylabel('空间位置 (y)')
ax.set_zlabel('空间位置 (z)')
ax.set_title('放射性废水三维扩散模拟及路径追踪')
plt.legend()
plt.show()
问题三思路
【更多思路扫描文章下方二维码获取~~】
第三个问题涉及到根据调查结果分析放射性废水对中国未来渔业经济的长期影响。
- 了解调查结果: 理解表格中的调查结果,包括废水排放前后中国居民对购买和食用海鲜的态度。
- 建立数学模型: 建立一个模型来描述放射性废水对中国渔业经济的长期影响。可以考虑使用影响因素如废水浓度、海鲜供应量等的模型。
- 数据分析: 分析调查结果,了解废水排放对居民购买和食用海鲜的影响。
- 模型验证: 使用实际数据验证建立的数学模型,确保模型与观察结果一致。
- 长期影响预测: 基于建立的模型,预测放射性废水对中国渔业经济的长期影响。
数学模型:
(1)供需模型
一个可能的数学模型是考虑废水浓度对海鲜市场需求的影响,可以建立海鲜市场的供需模型,考虑废水浓度、价格、人口变化等因素对市场需求和供应的影响。
该模型可以包括以下要素:
![]()
这里,Demand 是海鲜市场的需求,废水浓度是废水排放对海鲜的影响,其他因素可以包括价格、市场宣传等其他可能的因素。
import numpy as np
import matplotlib.pyplot as plt
# 模型参数
废水浓度 = np.linspace(0, 1, 100) # 废水浓度范围
其他因素 = np.random.rand(100) # 其他影响因素(随机生成)
# 模型函数
def 海鲜市场需求(废水浓度, 其他因素):
return 100 - 50 * 废水浓度 + 30 * 其他因素
# 计算需求
需求 = 海鲜市场需求(废水浓度, 其他因素)
# 绘制结果
plt.plot(废水浓度, 需求)
plt.xlabel('废水浓度')
plt.ylabel('海鲜市场需求')
plt.title('放射性废水对海鲜市场需求的影响模型')
plt.show()
(2)时间序列方法
也可以选择使用时间序列分析方法,考察海鲜市场需求和渔业经济变化的趋势,以预测未来的发展。
1、ARIMA 模型(Autoregressive Integrated Moving Average):
- 思路: 基于时间序列的自相关和移动平均性质,将序列的差分平稳化,再建立自回归和滑动平均的模型。
- Python 库:statsmodels 中的 ARIMA 模型。
from statsmodels.tsa.arima.model import ARIMA
model = ARIMA(data, order=(p, d, q))
results = model.fit()
predictions = results.predict(start=start_date, end=end_date, dynamic=False, typ='levels')
2、Prophet 模型:
- 思路: 由Facebook开发的时间序列预测模型,适用于具有季节性和趋势的数据。
- Python 库: prophet。
from fbprophet import Prophet
model = Prophet()
model.fit(dataframe)
future = model.make_future_dataframe(periods=365)
forecast = model.predict(future)
(3)机器学习方法
使用机器学习算法,对大量的调查数据进行训练,以预测放射性废水对渔业经济的长期影响。
- 线性回归模型:
思路: 基于输入特征的线性组合来建模。
Python 库: scikit-learn 中的 LinearRegression。
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)
- 决策树模型:
思路: 基于特征的阈值来进行决策,可处理非线性关系。
Python 库: scikit-learn 中的 DecisionTreeRegressor。
from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor()
model.fit(X_train, y_train)
predictions = model.predict(X_test)
- 随机森林模型:
思路: 由多个决策树组成,通过集成方法提高预测性能。
Python 库: scikit-learn 中的 RandomForestRegressor。
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor()
model.fit(X_train, y_train)
predictions = model.predict(X_test)
- 神经网络模型(深度学习):
思路: 使用深度神经网络进行端到端的学习。
Python 库: TensorFlow 或 PyTorch 中的深度学习框架。
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
model.add(Dense(units=64, activation='relu', input_dim=input_dim))
model.add(Dense(units=1, activation='linear'))
model.compile(optimizer='adam', loss='mean_squared_error')
model.fit(X_train, y_train, epochs=100, batch_size=32)
predictions = model.predict(X_test)
问题四思路
【更多思路扫描文章下方二维码获取~~】
问题五思路
【更多思路扫描文章下方二维码获取~~】
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 算法训练day32|贪心算法part02
- 10- OpenCV:基本阈值操作(Threshold)
- 淘宝/天猫商品详情实时数据API技术实现
- QModelIndex 是 Qt 框架中的一个类,用于表示数据模型中的索引位置
- Langchain模板-LangChainTemplates 讲解及应用
- HiddenDesktop:一款针对Cobalt Strike设计的HVNC隐藏桌面工具
- 云卷云舒:软件产品质量保证思考
- 【EI会议征稿】第三届算法、微芯片与网络应用国际会议(AMNA 2024)
- 使用Python Flask搭建一个简单的Web站点并发布到公网上访问
- 通过WinSW将windows可执行程序注册为windows服务