二叉树的深度和高度问题(算法村第八关白银挑战)
发布时间:2024年01月07日
二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
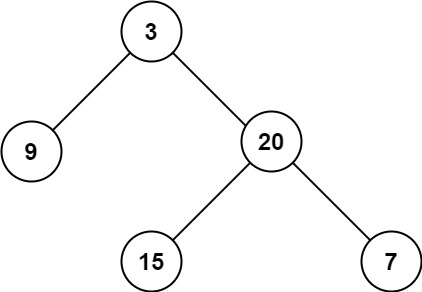
输入:root = [3,9,20,null,null,15,7]
输出:3
提示:
- 树中节点的数量在
[0, 104]区间内。
递归
对于根节点,它到叶结点的最大深度 = 1 + max(左节点的最大深度,右节点的最大深度)。所以,我们只需递归地求当前结点到叶结点的最大深度即可
public int maxDepth(TreeNode root)
{
//触底情况:访问叶结点的左右孩子
if (root == null)
return 0;
int leftDepth = maxDepth(root.left);
int rightDepth = maxDepth(root.right);
return 1 + Math.max(leftDepth, rightDepth);
}
层序遍历
最大深度也即二叉树的层数,所以我们可以采用层序遍历的方法,每遍历完一层就记录二叉树的层数。
public int maxDepth(TreeNode root)
{
if (root == null)
return 0;
int maxDepth = 0;
ArrayDeque<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
while (!queue.isEmpty())
{
//当前层的结点个数
int size = queue.size();
for (int i = 0; i < size; i++)
{
TreeNode curNode = queue.poll();
if (curNode.left != null)
queue.offer(curNode.left);
if (curNode.right != null)
queue.offer(curNode.right);
}
maxDepth++; //当前层遍历完毕,总层数+1
}
return maxDepth;
}
平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
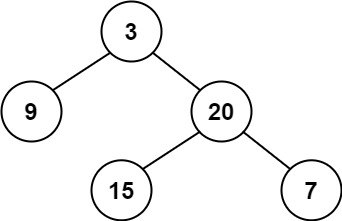
输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
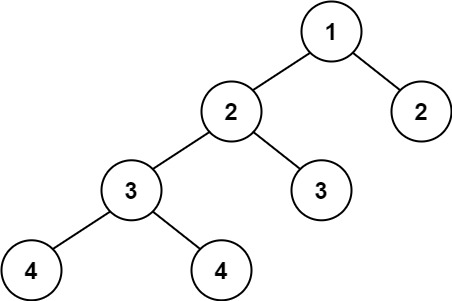
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
提示:
- 树中的节点数在范围
[0, 5000]内
求最大深度的过程中判断一下即可
public boolean isBalanced(TreeNode root)
{
//假设它是平衡二叉树,找找看有没有反例(只有反例才能一直保存)
boolean[] isBalanced = {true};
maxDepth(root, isBalanced);
return isBalanced[0];
}
public int maxDepth(TreeNode root, boolean[] isBalanced)
{
if (root == null)
return 0;
int leftDepth = maxDepth(root.left, isBalanced);
int rightDepth = maxDepth(root.right, isBalanced);
if(Math.abs(leftDepth - rightDepth) > 1)
isBalanced[0] = false;
return 1 + Math.max(leftDepth, rightDepth);
}
文章来源:https://blog.csdn.net/cjj2543107638/article/details/135442914
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- B端界面设计:查询表格页面
- springboot118共享汽车管理系统
- Springboot整合多数据源,Mybatis-plus,druid 的实现
- 服务器上配置jupyter,提示Invalid credentials如何解决
- Hadoop3.3.5云服务器安装教程-单机/伪分布式配置
- Rust语言第一篇:我是谁?
- 雪花算法-hutool也有
- GE1501 C++
- RocketMQ源码阅读-Message拉取与消费-Consumer篇
- 将毫秒数量转换为时分秒字符串(毫秒数→转换为→00:00:00.000形式)