【数据结构一】初始Java集合框架（前置知识）

Java中的数据结构

? ? ? ?Java语言在设计之初有一个非常重要的理念便是：write once，run anywhere！所以Java中的数据结构是已经被设计者封装好的了，我们只需要实例化出想使用的对象，便可以操作相应的数据结构了，本篇文章中我会向大家简单介绍一下什么是数据结构，以及对Java中常用的数据结构做简单介绍，在以后的文章中我会结合Java源码对Java中的每一个数据结构进行详细介绍并亲手实现，欢迎大家在评论区交流想法和意见啊。

目录

Java中的数据结构

1.什么是数据结构？

2.java中的数据结构（集合类）

3.java中的泛型

4.Java中Comparable和Comparator接口

5.时间和空间复杂度

---

1.什么是数据结构？

? ? ? ?数据结构是计算机中存储，组织数据的方式。我们现在学习的数据结构都是历史中总结出来的典型的优良的程序结构，在开发中多利用这些数据结构能显著提高你的代码质量。?

? ? ? ?我们需要学习的数据结构有：线性表，链表，堆，栈，队列，哈希表，二叉树，图等。

2.java中的数据结构（集合类）

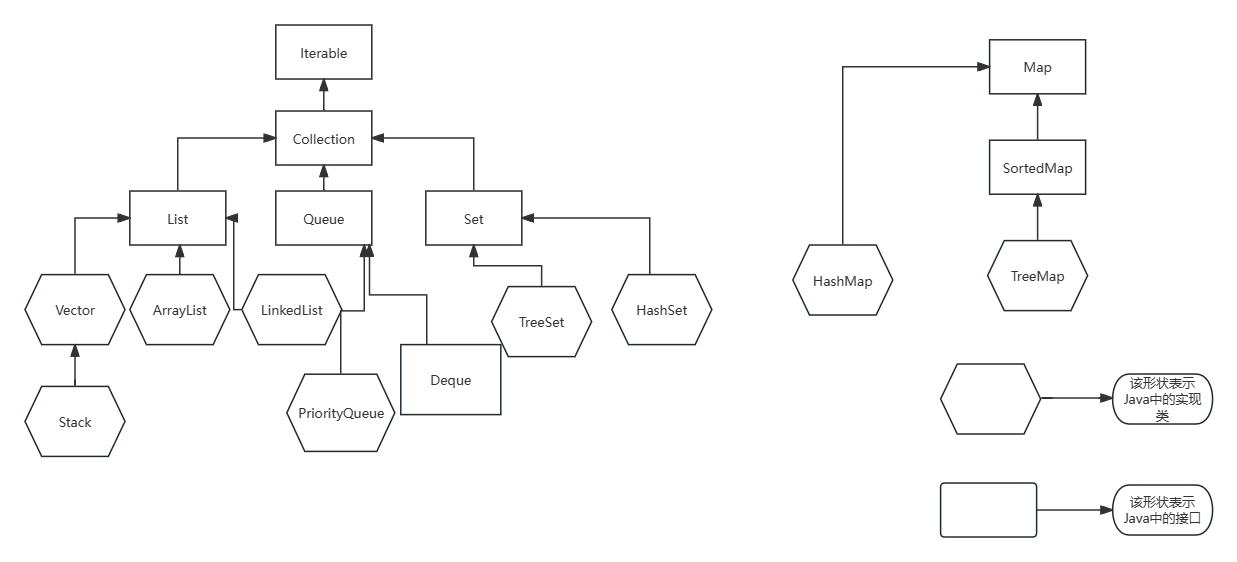
?上图中表示了Java中的集合框架，大致可以分为list，set，map三种体系：

1. Iterable：这是Java中负责迭代遍历的一个接口，内部包含了遍历的一些方法。
2. Collection：一个接口，包含了大部分容器常用的一些方法
3. List：一个接口，规范了ArrayList和Linkedlist中要实现的方法??
4. ArrayList：Java中最常用的集合类,底层为动态类型顺序表。
5. LinkedList ：实现了list接口，底层为双向链表。
6. Stack：底层是栈，栈是一种特殊的顺序表。
7. Queue：底层是队列，队列是一种特殊的顺序表。
8. Deque：一个接口，实现了双向队列的方法。
9. PriorityQueue：堆（又称为优先级队列），实现类，内部可按照大小堆的模式实现排序。
10. Set：一个接口，不能储存相同元素。
11. HashSet：底层为哈希桶，查询的时间复杂度是O(1);
12. TreeSet：底层是红黑树，查询的时间复杂度是O(log2 N),内部数据有序。
13. ? ? Map：一个接口，里面存储的是K-V模型的键值对
14. HashMap：底层为哈希桶，查询时间复杂度为O(1)
15. TreeMap：底层为红黑树，查询的时间复杂度为O(log2 N),内部数据有序。

3.java中的泛型

这个我准备在JavaSE专栏专门写一篇进行讲解，明天我会挂上链接。

4.Java中Comparable和Comparator接口

联系：

两者都是接口，都是Java中用来进行类型排序的。两者的排序方法均是通过相减返回一个int值，

返回正数，零和负数分别代表大于，等于和小于。

区别：

1. 字面区别：comparable是比较的意思，表示自身具备着某种能力。而comparator是比较器的意思，表示自身是比较的参与者。
2. 用法不同：comparable是由重写compareTo方法实现排序的，如果自定义类没有实现该接口是不能通过Collections.sort方法和Arrays.sort方法进行排序的。而comparator是由重写compare方法实现排序的，可以通过创建自定义比较器或者匿名内部类快捷创建比较器来实现比较。。
3. 使用场景不同：Comparable必须由自定义类内部实现排序方法，而Comparator无需修改原有类。Comparable可以看做对内进行排序接口，而comparator是对外进行排序的接口。

5.时间和空间复杂度

学习时间和空间复杂度的作用主要是帮助我们去分析一个数据结构或算法的优缺点，从这两方面来衡量一个算法的好坏。

1. 时间复杂度：我们用O（）表示

   // 计算func2的时间复杂度？
   void func2(int N) {
   int count = 0;
   for (int k = 0; k < 2 * N ; k++) {
   count++;
   }
   int M = 10;
   while ((M--) > 0) {
   count++;
   }
   System.out.println(count);
   }

   在实际中一般情况关注的是算法的最坏运行情况上述为2N+10次，所以上述代码中时间复杂度为O（N），一般都是粗略表示。
2. 空间复杂度：同样也是大O渐进表示法来表示

   // 计算fibonacci的空间复杂度？
   int[] fibonacci(int n) {
   long[] fibArray = new long[n + 1];
   fibArray[0] = 0;
   fibArray[1] = 1;
   for (int i = 2; i <= n ; i++) {
   fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
   }
   return fibArray;
   }

   上述代码中动态开辟了N个空间，空间复杂度为O（N）。