《数字信号处理》——IIR数字滤波器的设计

目录

一、问题描述

二、项目任务

三、系统分析

3.1? 总体分析

3.2? 确定滤波器性能指标

3.3 设计模拟低通滤波器

3.4 模拟滤波器映射到数字滤波器

?3.5 本次使用冲激响应不变法

3.6 用实现的滤波器对信号进行滤波

四、系统设计与实现

4.1? 滤波器性能指标的转换

4.2? 模拟滤波器的实现

4.3 数字滤波器的实现

4.4 对输入信号进行滤波

五、系统结果分析?

六、总结

七、参考文献

八、完整项目代码

---

一、问题描述

????????数字滤波器是对数字信号进行滤波处理以得到期望的响应特性的离散时间系统，理论上可以实现任何可以用数学算法表示的滤波效果。随着集成电路成本的不断降低，数字滤波器已经成为高级无线通信系统、相控阵雷达雷达、目标控制与导航系统等关键设备的重要组成部分。其中IIR数字滤波器采用递归型结构，带有反馈环路，其运算结构通常由延时、乘以系数和相加等基本运算组成，可以组合成直接型、正准型、级联型、并联型四种结构形式。同学们在设计IIR数字滤波器在设计时，可以借助成熟的模拟滤波器的成果，如巴特沃斯、契比雪夫和椭圆滤波器等，运用 MATLAB 设计 IIR 数字低通滤波器，进而实现信号滤波。

二、项目任务

任务1、设计一模拟 IIR 模拟低通滤波器并转换为数字 IIR 低通滤波器。

说明:

（1）模拟滤波器设计采用巴特沃斯模拟滤波器。

（2）模拟到数字转换采用冲激响应或者双线性映射法。

任务 2、利用实现的滤波器对信号进行滤波。(考核扩展功能部分)

提示：完成此步骤需要与任务一综合考虑。分析有用和噪音信号的频率，并参考噪音信号的频率利用采样定理等知识选取合理的滤波器截止频率进行任务一的设计。

三、系统分析

3.1? 总体分析

????????设计一个数字IIR低通滤波器，可以采取先设计模拟IIR低通滤波器，后转换为数字滤波器的方式：
? ? ? ?首先，确定滤波器性能指标。将给定的数字低通滤波器的性能指标转换为模拟低通滤波器的性能指标。
? ? ? ?其次，按照模拟低通滤波器的性能指标设计模拟低通滤波器。
? ? ? ?然后，将模拟滤波器的传输函数转换为数字滤波器的系统函数。
? ? ? ?最后，利用实现的滤波器对信号进行滤波。

3.2? 确定滤波器性能指标

????????数字低通滤波器的性能指标有通带截止频率wp、通带最大衰减系数δp、阻带截止频率ws、阻带最小衰减系数δs，具体可体现在以下的低通滤波器幅度响应的容限图中，即图1：

?图1? 理想低通滤波器逼近的误差容限

????????而模拟低通滤波器的性能指标为通带截止频率Ωp、通带最大衰减系数δp、阻带截止频率Ωs、阻带最小衰减系数δs。根据已知的数字低通滤波器的性能指标，经过转换后得到的模拟低通滤波器的性能指标Ωp、δp、Ωs、δs是设计模拟低通滤波器所需的。数字滤波器的性能指标与模拟滤波器性能指标的转换方法主要有两种方法，分别为冲激响应不变法和双线性映射法。
? ? ? ?本次使用冲激响应不变法！冲激响应不变法的性能指标对应关系如下所示，其中Ω为模拟角频率，w为数字角频率，f为频率，T为对模拟信号的采样周期，Fs为采样频率：?

?

3.3 设计模拟低通滤波器

????????对于模拟滤波器的设计，一般都先设计一个归一化原型低通滤波器，再通过频带变化将
其转换为所需类型的模拟滤波器，此处我们选定的模拟滤波器类型为巴特沃斯低通滤波器。
首先设计原型低通滤波器，即将低通通带边沿频率归一化为1。对于巴特沃斯滤波器，
将3dB 衰减处的频率Ωc 归一化为1。在确定了所需滤波器的性能指标后，可以求出滤波器
的阶数N，再求出归一化的低通原型滤波器的Han(s)，最后将Han(s)转换为所需类型的低
通滤波器系统函数Ha(s)，可由图2 表示：??

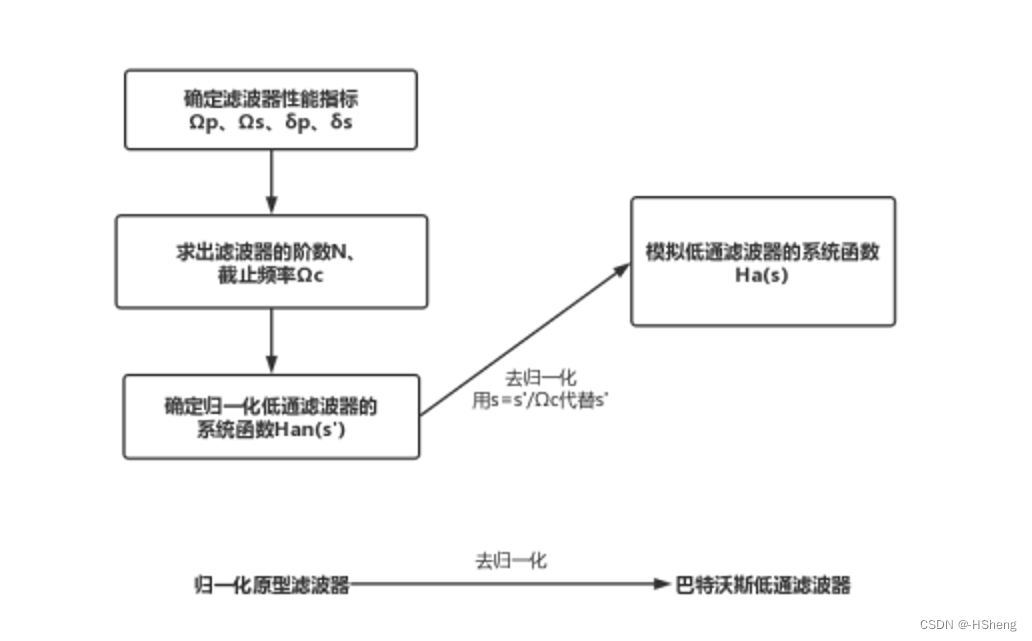?图2? 模拟低通滤波器设计思路

3.4 模拟滤波器映射到数字滤波器

映射本质即从s平面映射到z平面，映射需要满足以下两个条件。
（1）映射前后的频率相对应，即

?

（2）因果稳定的Ha(s)必须映射成因果稳定的H(z)，即

?3.5 本次使用冲激响应不变法

????????冲激响应不变法是将模拟滤波器的单位冲激响应ha(t)映射成数字滤波器的单位冲激响应h(n)，使得h(n)等于ha(t)的采样值。
? ? ? ??在已知Ha(s)的情况下，将其展成部分分式的形式，从而可以利用拉普拉斯逆变换得到对应的冲激响应ha(t)。然后对ha(t)进行等间隔采样，从而得到h(n)。最后对h(n)进行z变换，得到数字滤波器的系统函数H(z)。可由图3所示：

?图3 冲激响应不变法?

????????若模拟滤波器频率响应不带限于±Π/T，则会在±Π/T的奇数倍附近产生频率混叠。故应该设定|Ω|≥±Π/T。采用非线性频率压缩方法，将整个频率轴上的频率范围压缩到（-Π/T，+Π/T）之间。

3.6 用实现的滤波器对信号进行滤波

????????输入信号由四个频率不同的余弦信号以及一个随机信号进行混频，混频后用y表示，再用实现的滤波器对混频信号进行滤波。
? ? ? ?对输入信号进行快速傅里叶变换（FFT）后，得到输入信号的频域图像。同样，对滤波后的信号也进行FFT得到频域图像。将二者比较，观察滤波器的作用，并且在此基础上，更改滤波器的性能指标，从而找到最佳的性能指标。

四、系统设计与实现

4.1? 滤波器性能指标的转换

????????给定数字滤波器的性能指标通带截止频率wp为0.1Π、通带最大衰减系数δp为3、阻带截止频率ws为0.5Π、阻带最小衰减系数δs为15，经过转换得到模拟滤波器的性能指标通带截止频率Ωp、通带最大衰减系数δp、阻带截止频率Ωs、阻带最小衰减系数δs。使用冲激响应不变法转换的代码如下所示：

clc;
Td=0.1;Fs=1/Td;%Td为对模拟信号的采样周期，Fs为采样频率
Wp=0.1*pi;%数字低通的技术指标，通带截止频率，为数字角频率
Ws=0.5*pi;%阻带截止频率
Rp=3;%通带最大衰减
As=15;%阻带最小衰减
Omegap=Wp/Td;%模拟低通的技术指标，模拟角频率
Omegas=Ws/Td;

4.2? 模拟滤波器的实现

????????本次设计选用的原型模拟滤波器为巴特沃斯滤波器，具体调用buttord和buttap两个函数。buttord函数用于求出滤波器阶数N和3dB截止频率（Ωc），而buttap用于设计N阶巴特沃斯低通原型滤波器的零、极点。具体代码如下：

[N,Omegac]=buttord(Omegap,Omegas,Rp,As,’s’);
%生成巴特沃斯滤波器的阶次N和截止频率Omegac
[z0,p0,k0]=buttap(N);
%设计巴特沃斯低通原型滤波器

?????????将原型模拟滤波器转换为低通模拟滤波器，需要调用zp2tf和lp2lp两个函数。zp2tf函数用于将零极点增益的滤波器参数转换为传递函数的形式，而lp2lp函数用于实现低通模拟原型滤波器至低通滤波器的转换。具体代码如下所示：

[Bap,Aap]=zp2tf(z0,p0,k0);
%将零极点增益的滤波器参数转换为传递函数的形式
%Bap为传递函数的分子系数，Aap为父母系数
[b,a]=lp2lp(Bap,Aap,Omegac)
%实现低通模拟原型滤波器至低通滤波器的转换

4.3 数字滤波器的实现

????????利用冲激响应不变法实现模拟滤波器转换为数字滤波器，需要调用impinvar函数，此函数的功能就是利用冲激响应不变法将模拟滤波器转换为数字滤波器。具体代码如下：

[bz,az]=impinvar(b,a,Fs);
%冲激响应不变法
%将模拟滤波器传递函数模型转换为采样频率为Fs的数字滤波器传递函数

利用freqz函数画出数字滤波器的频率响应图像，具体代码如下：

[H,W]=freqz(bz,az,512,Fs);%数字滤波器的频率响应
%bz为系统函数分子系数，az为分母系数，512为频率点数
figure;%创建图窗窗口
plot(W,20*log10(abs(H)));%abs(H)为幅度
%这里画出了数字低通滤波器的幅频曲线
grid on;%显示网格线
title('数字滤波器的幅频曲线');
xlabel('频率/Hz');
ylabel('幅度/dB');

?运行结果展示如下（滤波器的幅频曲线）所示

?图4 ?冲激响应不变法下的滤波器幅频曲线

4.4 对输入信号进行滤波

????????输入信号中的四个余弦信号幅度分别为f1=15Hz、f2=30Hz、f3=45Hz、f4=60Hz，随机信号调用randn函数来生成，具体代码如下：

f1=15;%第一个点频信号分量频率
f2=30;%第二个点频信号分量频率
f3=45;%第三个点频信号分量频率
f4=60;%第四个点频信号分量频率
fs=100;%采样频率
T=2;%间隔长度
n=round(T*fs);%round函数为四舍五入的取整函数，n为采样点个数
t=linspace(0,T,n);%将(0.T)分为n份
y=2*cos(2*pi*f1*t)+cos(2*pi*f2*t)+cos(2*pi*f3*t)+cos(2*pi*f4*t)+randn(size(t));
%randn(size(t))表示返回一个与t相同尺寸的随机矩阵

????????将输入信号的时域图像和频域图像分别画出，后者需要调用fftshift和fft两个函数。fftshift函数用于将零谱点移到频谱中间，而fft函数即进行快速傅里叶变换，具体代码如下：

时域图像代码：

figure;
subplot(2,1,1);
plot(t,y);
title('输入信号时域图像');
xlabel('t/s');
ylabel('y');

?频域图像代码：

fft_y=fftshift(fft(y));
%fftshift表示将零谱点移到频谱中间，fft即进行快速傅里叶变换
f=linspace(-fs/2,fs/2,n);
subplot(2,1,2);
plot(f,abs(fft_y));%画出幅度频率曲线
title('输入信号频域图像');%表示此为滤波前的
xlabel('f/Hz');
ylabel('y');
axis([ 0 50 0 100]);

?运行结果， 输入信号的时域图像和频域图像如下图所示：

?

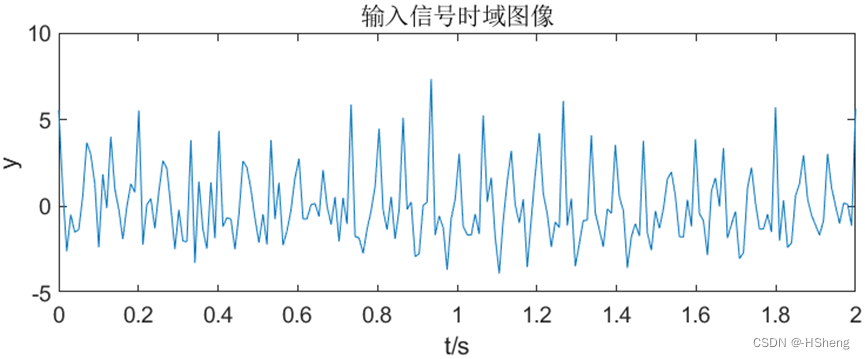
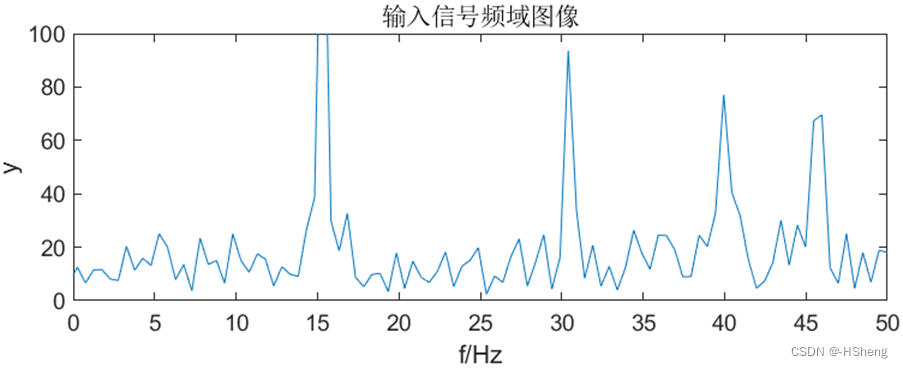??图5 输入信号的时域图像和频域图像

????????将输入信号经实现的滤波器进行滤波后，分别画出输出信号的时域图像和频域图像。需要调用filter函数，此函数的作用是实现差分方程的仿真，在此即进行滤波作用，具体代码如下所示：?

figure;
final=filter(bz, az, y);%进行滤波
subplot(2,1,1);
plot(t,final);
title('滤波后的时域图像');%表示此为滤波后的
xlabel('t/s');
ylabel('y');

finall=fftshift(fft(final));
subplot(2,1,2);
plot(f,abs(finall));
title('滤波后的频域图像');
axis([ 0 50 0 100]);

?运行结果，经过滤波后冲激响应不变法下输出信号的时域图像和频域图像如下：

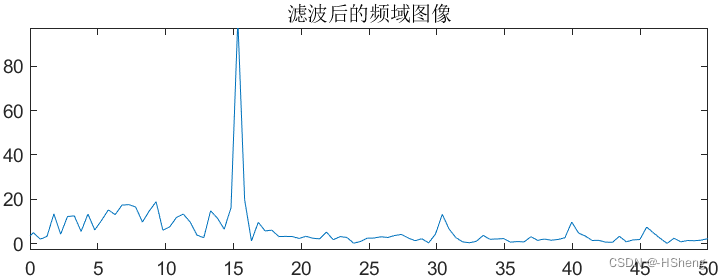
图6? 冲激响应不变法下输出信号?

五、系统结果分析?

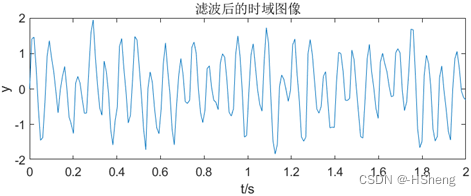
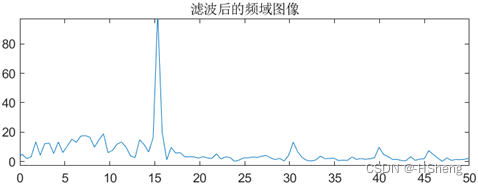
（1）对于数字滤波器的性能指标通带截止频率wp 为0.1Π、通带最大衰减系数δp 为3、阻带截止频率ws 为0.5Π、阻带最小衰减系数δs 为15 的给定下，根据仿真结果可以看到如图7，可看出得到的数字滤波器已经可以将f1=15Hz 的正弦波基本保留，对于f2=30Hz、f3=45Hz、f4=60Hz 的正弦波大大衰减，但仍有部分保留。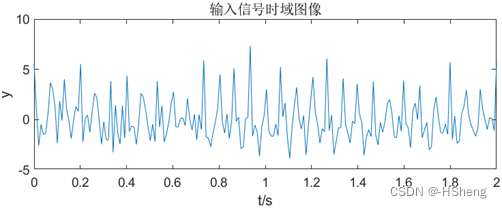
?

?

?

（2）现改变数字滤波器的性能指标，从而对比观察：
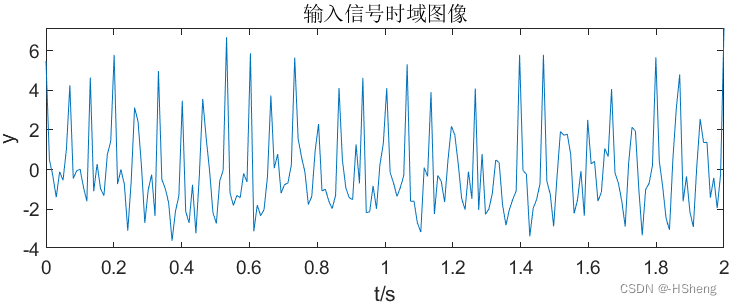
????????使得wp=0.2Π、δp=3、ws=0.4Π、δs=17，仿真结果如图8。可以看出数字滤波器已经可以将f1=15Hz 的正弦波基本保留，对于f2=30Hz 大大衰减，但仍有少部分保留，而对于f3=45Hz、f4=60Hz 的正弦波几乎完全被消除。?

?

?

?

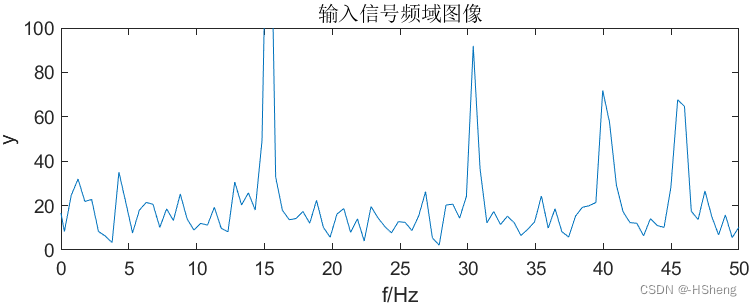
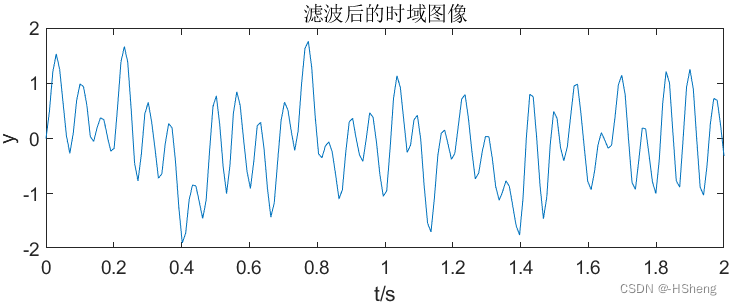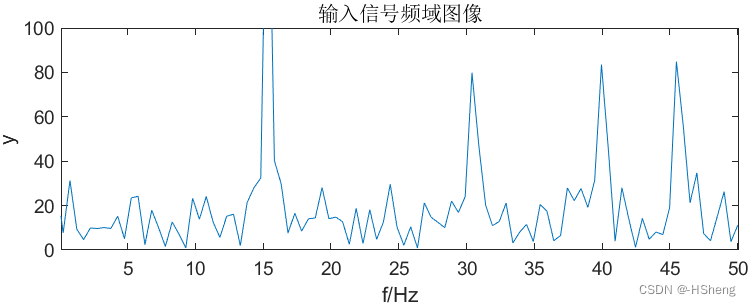
????????(3) 使得wp=0.3Π、δp=3、ws=0.35Π、δs=19，仿真结果如图9。可以看出数字滤波器已经可
以将f1=15Hz 的正弦波完全保留，对于f2=30Hz、f3=45Hz、f4=60Hz 的正弦波完全被消除。?

?

?

?

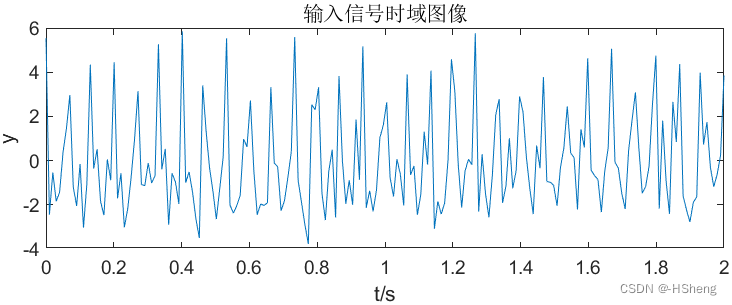六、总结

（1）总结：

????????在我的IIR滤波器设计中，我选择了一种间接的方法。具体而言，我首先设计了一个归一化样本模拟低通滤波器，然后通过频率变换将其转换为模拟低通滤波器，最终再将其转换为数字低通滤波器。相较之下，还有一种直接转换的方法，即结合频率转换和数字化，直接将样本模拟低通滤波器转换为数字低通滤波器。

????????在进行模拟与数字的转换时，我运用了冲激响应不变法。在这个过程中，我发现通过缩短过渡区域并增大阻带的衰减系数，可以使得幅频曲线更加陡峭。这样的调整会导致滤波器的阶数增加，从而提高了滤波器的效果。

????????另一种可行的方法是使用双线性映射法，尽管在本次大作业中我并未选择这种方式进行设计。然而，即便采用双线性映射法，之前的结论仍然成立。尽管在相同技术指标下，同一阶数的滤波器采用双线性映射法效果较好，但这种方法也存在一些问题。虽然它成功克服了多值映射的关系，能够消除频率混叠，但会带来更大的负的相位裕度，并引入杂频，从而对滤波效果产生一定影响。这说明，滤波效果与滤波速度之间的平衡在设计中需要谨慎权衡。

（2）心得体会：

????????在本次IIR数字滤波器设计的过程中，我温习和学到了很多关于数字信号处理和滤波器设计的知识和技巧。通过实践操作，我对IIR数字滤波器的工作原理、设计方法和性能特点有了更深入的了解。在此，我对整个设计过程分享一些心得体会。

????????（1）理论学习：在进行IIR数字滤波器设计之前，我首先对数字信号处理和滤波器设计的基本原理进行了温习。这包括离散时间信号与系统、滤波器的基本概念、分类和特性等。这些理论知识为我后续的设计工作打下了坚实的基础。

????????（2）IIR数字滤波器原理：IIR（Infinite Impulse Response，无限脉冲响应）数字滤波器是一种具有无限脉冲响应的滤波器，其特点是具有线性相位特性，且系统函数为有理函数。IIR数字滤波器的设计方法主要有巴特沃斯法、切比雪夫法、椭圆法等。

????????（3）设计步骤：在本次设计中，我采用了MATLAB软件进行IIR数字滤波器的设计。设计过程主要包括确定滤波器的性能指标、选择合适的设计方法和计算滤波器的系数等。在设计过程中，我学会了如何根据实际需求调整滤波器的参数，以实现最佳的滤波效果。

????????（4）性能分析：在设计完成后，我对所设计的IIR数字滤波器进行了性能分析，包括幅频响应、相频响应、群延迟等。通过对滤波器性能的分析，我可以更好地了解滤波器的特性，并为后续的优化和改进提供依据

????????（5）总体而言，通过这次IIR数字滤波器设计的经历，我不仅提高了对信号处理的理解，还培养了解决复杂工程问题的能力。这是一次富有挑战性的学习经历，使我更加深入地了解了数字滤波器设计的方方面面。

七、参考文献

（1）实验六 基于 MATLAB的 IIR数字滤波器设计 _bilinear函数 matlab-CSDN博客
（2）如何通俗易懂地理解 FIR/IIR滤波器？ - 知乎 (zhihu.com)
（3）IIR数字滤波器设计（数字信号处理） - 知乎 (zhihu.com)
（4）IIR与 FIR数字滤波器设计 _iir滤波器和 fir滤波器的设计过程 -CSDN博客
（5）学习随笔之 IIR滤波器与 FIR滤波器 - 知乎 (zhihu.com)
（6）什么是巴特沃斯滤波器 - 知乎 (zhihu.com)
（7）基于巴特沃斯的数字低通滤波器设计 -CSDN博客?

八、完整项目代码

clc;
Td=0.1;Fs=1/Td;%Td为对模拟信号的采样周期，Fs为采样频率
Wp=0.1*pi;%数字低通的技术指标，通带截止频率，为数字角频率
Ws=0.5*pi;%阻带截止频率
Rp=3;%通带最大衰减
As=15;%阻带最小衰减
Omegap=Wp/Td;%模拟低通的技术指标，模拟角频率
Omegas=Ws/Td;

[N,Omegac]=buttord(Omegap,Omegas,Rp,As,'s');
%生成巴特沃斯滤波器的阶次N和截止频率Omegac
[z0,p0,k0]=buttap(N);
%设计巴特沃斯低通原型滤波器

[Bap,Aap]=zp2tf(z0,p0,k0);
%将零极点增益的滤波器参数转换为传递函数的形式
%Bap为传递函数的分子系数，Aap为父母系数
[b,a]=lp2lp(Bap,Aap,Omegac)
%实现低通模拟原型滤波器至低通滤波器的转换

[bz,az]=impinvar(b,a,Fs);
%冲激响应不变法
%将模拟滤波器传递函数模型转换为采样频率为Fs的数字滤波器传递函数

[H,W]=freqz(bz,az,512,Fs);%数字滤波器的频率响应
%bz为系统函数分子系数，az为分母系数，512为频率点数
figure;%创建图窗窗口
plot(W,20*log10(abs(H)));%abs(H)为幅度
%这里画出了数字低通滤波器的幅频曲线
grid on;%显示网格线
title('数字滤波器的幅频曲线');
xlabel('频率/Hz');
ylabel('幅度/dB');

f1=15;%第一个点频信号分量频率
f2=30;%第二个点频信号分量频率
f3=45;%第三个点频信号分量频率
f4=60;%第四个点频信号分量频率
fs=100;%采样频率
T=2;%间隔长度
n=round(T*fs);%round函数为四舍五入的取整函数，n为采样点个数
t=linspace(0,T,n);%将(0.T)分为n份
y=2*cos(2*pi*f1*t)+cos(2*pi*f2*t)+cos(2*pi*f3*t)+cos(2*pi*f4*t)+randn(size(t));
%randn(size(t))表示返回一个与t相同尺寸的随机矩阵

figure;
subplot(2,1,1);
plot(t,y);
title('输入信号时域图像');
xlabel('t/s');
ylabel('y');

fft_y=fftshift(fft(y));
%fftshift表示将零谱点移到频谱中间，fft即进行快速傅里叶变换
f=linspace(-fs/2,fs/2,n);
subplot(2,1,2);
plot(f,abs(fft_y));%画出幅度频率曲线
title('输入信号频域图像');%表示此为滤波前的
xlabel('f/Hz');
ylabel('y');
axis([ 0 50 0 100]);

figure;
final=filter(bz, az, y);%进行滤波
subplot(2,1,1);
plot(t,final);
title('滤波后的时域图像');%表示此为滤波后的
xlabel('t/s');
ylabel('y');

finall=fftshift(fft(final));
subplot(2,1,2);
plot(f,abs(finall));
title('滤波后的频域图像');
axis([ 0 50 0 100]);

?