CNN——LeNet

1.LeNet概述? ? ? ?

?????????LeNet是Yann LeCun于1988年提出的用于手写体数字识别的网络结构，它是最早发布的卷积神经网络之一，可以说LeNet是深度CNN网络的基石。

????????当时，LeNet取得了与支持向量机（support vector machines）性能相媲美的成果，成为监督学习的主流方法。 LeNet当时被广泛用于自动取款机（ATM）机中，帮助识别处理支票的数字。

? ? ? ? 下面是整个网络的结构图

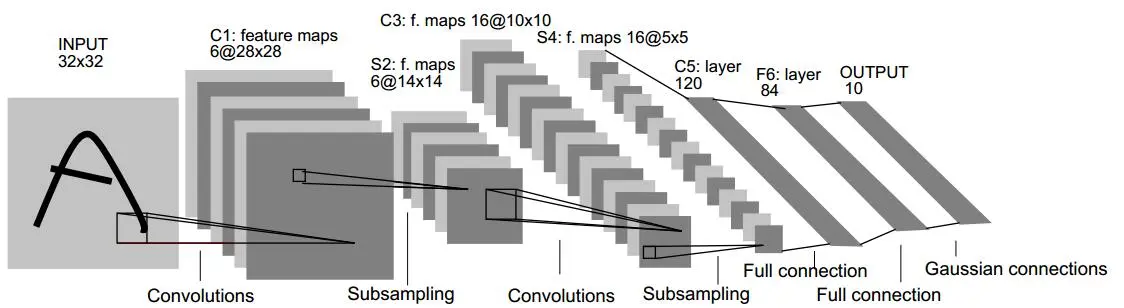
????????LeNet共有8层，其中包括输入层，3个卷积层，2个子采样层（也就是现在的池化层），1个全连接层和1个高斯连接层。

????????上图中用C代表卷积层，用S代表采样层，用F代表全连接层。输入size固定在1*32*32，LeNet图片的输入是二值图像。网络的输出为0~9十个数字的RBF度量，可以理解为输入图像属于0~9数字的可能性大小。

2.详解LeNet

下面对图中每一层做详细的介绍：

• LeNet使用的卷积核大小都为5*5，步长为1，无填充，只是卷积深度不一样(卷积核个数导致生成的特征图的通道数)
• 激活函数为Sigmoid
• 下采样层都是使用最大池化实现，池化的核都为2*2，步长为2，无填充

? ? ? ? input输入层，尺寸为1*32*32的二值图

????????C1层是一个卷积层。该层使用6个卷积核，生成特征图尺寸为32-5+1=28，输出为6个大小为28*28的特征图。再经过一个Sigmoid激活函数非线性变换。

????????S2层是一个下采样层。生成特征图尺寸为28/2=14，得到6个14*14的特征图。

????????C3层是一个卷积层，该层使用16个卷积核，生成特征图尺寸为14-5+1=10，输出为16个10*10的特征图。再经过一个Sigmoid激活函数非线性变换。

????????S4层是一个下采样层，生成特征图尺寸为10/2=5，得到16个5*5的特征图

????????C5层是一个卷积层，卷积核数量增加至120。生成特征图尺寸为5-5+1=1。得到120个1*1的特征图。这里实际上相当于S4全连接了，但仍将其标为卷积层，原因是如果LeNet-5的输入图片尺寸变大，其他保持不变，那该层特征图的维数也会大于1*1，那就不是全连接了。再经过一个Sigmoid激活函数非线性变换。

????????F6层是一个全连接层，该层与C5层全连接，输出84张特征图。再经过一个Sigmoid激活函数非线性变换。

????????输出层：输出层由欧式径向基函数（高斯）单元组成，每个类别（0~9数字）对应一个径向基函数单元，每个单元有84个输入。也就是说，每个输出RBF单元计算输入向量和该类别标记向量之间的欧式距离，距离越远，PRF输出越大，同时我们也会将与标记向量欧式距离最近的类别作为数字识别的输出结果。当然现在通常使用的Softmax实现。

3.使用LeNet实现Mnist数据集分类

1.导入所需库

import torch
import torch.nn as nn
from torchsummary import summary
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
from tqdm import tqdm # 显示训练进度条

2.使用GPU

device = 'cuda' if torch.cuda.is_available() else 'cpu'

3.读取Mnist数据集

# 定义数据转换以进行数据标准化
transform = transforms.Compose([
    transforms.ToTensor(),  # 将图像转换为 PyTorch 张量
])

# 下载并加载 MNIST 训练和测试数据集
train_dataset = datasets.MNIST(root='./dataset', train=True, download=True, transform=transform)
test_dataset = datasets.MNIST(root='./dataset', train=False, download=True, transform=transform)

# 创建数据加载器以批量加载数据
batch_size = 256
train_dataloader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_dataloader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)

4.搭建LeNet

? ? ? ? 需要注意的是torch.nn.CrossEntropyLoss自带了softmax函数，所以最后一层使用全连接即可，在训练时使用torch.nn.CrossEntropyLoss

class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        self.conv1 = nn.Conv2d(1, 6, kernel_size=5, padding=2) # Mnist尺寸为28*28，这里设置填充变成32*32
        self.sigmoid = nn.Sigmoid()
        self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
        self.conv2 = nn.Conv2d(6, 16, kernel_size=5)
        self.flatten = nn.Flatten()
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(self.sigmoid(self.conv1(x)))
        x = self.pool(self.sigmoid(self.conv2(x)))
        x = self.flatten(x)
        x = self.sigmoid(self.fc1(x))
        x = self.sigmoid(self.fc2(x))
        x = self.fc3(x)
        return x
# 实例化模型
model = LeNet().to(device)
summary(model, (1, 28, 28))

5.训练函数

def train(model, lr, epochs):
    # 将模型放入GPU
    model = model.to(device)
    # 使用交叉熵损失函数
    loss_fn = nn.CrossEntropyLoss().to(device)
    # SGD
    optimizer = torch.optim.SGD(model.parameters(), lr=lr)
    # 记录训练与验证数据
    train_losses = []
    train_accuracies = []
    # 开始迭代   
    for epoch in range(epochs):   
        # 切换训练模式
        model.train()  
        # 记录变量
        train_loss = 0.0
        correct_train = 0
        total_train = 0
        # 读取训练数据并使用 tqdm 显示进度条
        for i, (inputs, targets) in tqdm(enumerate(train_dataloader), total=len(train_dataloader), desc=f"Epoch {epoch+1}/{epochs}", unit='batch'):
            # 训练数据移入GPU
            inputs = inputs.to(device)
            targets = targets.to(device)
            # 模型预测
            outputs = model(inputs)
            # 计算损失
            loss = loss_fn(outputs, targets)
            # 梯度清零
            optimizer.zero_grad()
            # 反向传播
            loss.backward()
            # 使用优化器优化参数
            optimizer.step()
            # 记录损失
            train_loss += loss.item()
            # 计算训练正确个数
            _, predicted = torch.max(outputs, 1)
            total_train += targets.size(0)
            correct_train += (predicted == targets).sum().item()
        # 计算训练正确率并记录
        train_loss /= len(train_dataloader)
        train_accuracy = correct_train / total_train
        train_losses.append(train_loss)
        train_accuracies.append(train_accuracy)

        # 输出训练信息
        print(f"Epoch [{epoch + 1}/{epochs}] - Train Loss: {train_loss:.4f}, Train Acc: {train_accuracy:.4f}")
    # 绘制损失和正确率曲线
    plt.figure(figsize=(10, 5))
    plt.subplot(1, 2, 1)
    plt.plot(range(epochs), train_losses, label='Training Loss')
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    plt.legend()
    plt.subplot(1, 2, 2)
    plt.plot(range(epochs), train_accuracies, label='Accuracy')
    plt.xlabel('Epoch')
    plt.ylabel('Accuracy')
    plt.legend()
    plt.tight_layout()
    plt.show()

6.模型训练

model = LeNet()
lr = 0.9
epochs = 20
train(model,lr,epochs)

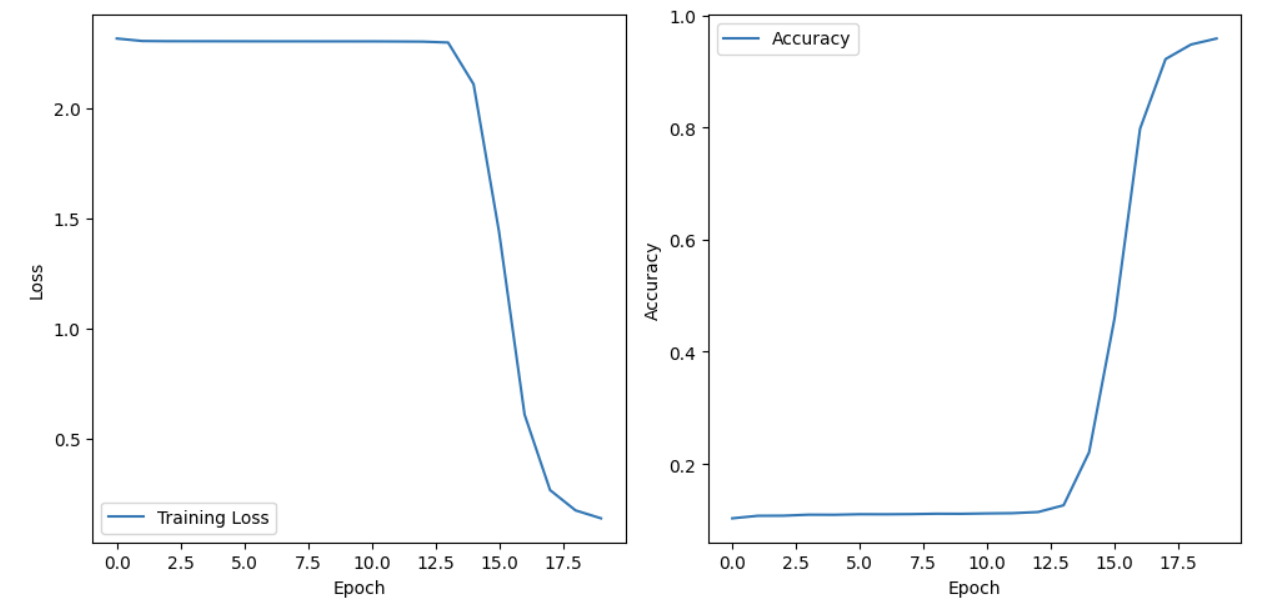
7.模型测试?

def test(model):
    model.eval()
    model.to(device)
    correct_test = 0
    total_test = 0
    with torch.no_grad():
        for inputs, targets in test_dataloader:  
            inputs = inputs.to(device)
            targets = targets.to(device)
            outputs = model(inputs)
            _, predicted = torch.max(outputs, 1)
            total_test += targets.size(0)
            correct_test += (predicted == targets).sum().item()
    test_accuracy = correct_test / total_test
    print(f"Accuracy on Test: {test_accuracy:.4f}")
    return test_accuracy

test(model)