【K12】python用科学函数写方程解串联电路问题
发布时间:2024年01月18日
物理例题:

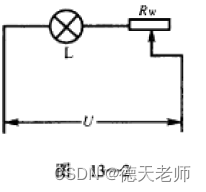
代码分析
构造方程:
from sympy中导包:Eq(),solve()
列方程函数
Eq()列方程函数
列出I2R=P,这里设置P为1

解方程函数
solve((方程1,方程2,方程3),(未知量1,已知量2,未知量3),返回字典)

多变量赋值
使用symbols()进行赋值,这里没有给出具体的值,只是用了原来字母本身的字符进行赋值。
V, R1, R2 = symbols(‘V R1 R2’)
from sympy import symbols, Eq, solve, sqrt
# 定义变量
R_L = 10 # 灯泡电阻
V, R1, R2 = symbols('V R1 R2')
# 建立方程组
equation1 = Eq((V / (R1 + R_L))**2 * R_L, 1) # 假设第一次灯泡功率为1(标幺值)
equation2 = Eq((V / (R2 + R_L))**2 * R_L, 1/4) # 第二次灯泡功率为1/4
equation3 = Eq(R1, 7) # 第一次滑动变阻器阻值为5Ω
# 使用solve解方程组
solutions = solve((equation1, equation2, equation3), (V, R1, R2), dict=True)
# 筛选R2和V同时大于0的解,并保留1位小数
valid_solutions = [sol for sol in solutions if sol[R2] > 0 and sol[V] > 0]
valid_solutions = [{k: round(float(v), 1) for k, v in sol.items()} for sol in valid_solutions]
if valid_solutions:
answer = valid_solutions[0][R2]
print(f"计算结果为:", valid_solutions)
print(f"所以,当灯泡功率变为原来的1/4时,滑动变阻器的阻值为:{answer}Ω。")
else:
print("没有找到满足条件的解。")
代码总结
这是一段对物理方程求解的串联电路问题,主要学习列方程 方程名变量,方程式,结果,还有解方程,方程结果存储变量,要注意参数:方程名称,变量名称,返回值是这段代码的核心。
SymPy
是一个强大的Python库,用于进行符号计算。它提供了广泛的函数和工具,可用于代数运算、微积分、矩阵操作、离散数学、量子物理等领域。SymPy库使得数学家、科学家和工程师能够轻松地进行复杂的数学计算,并以可读的方式呈现结果。
在本文中,我们深入探讨了SymPy库的功能和用法。我们介绍了如何定义符号、建立方程、进行代数运算、求解方程、计算微分和积分等基本操作。我们还探讨了如何使用SymPy处理矩阵和行列式、进行逻辑运算、简化表达式等高级功能。
通过使用SymPy库,我们能够快速准确地解决复杂的数学问题,无需手动执行繁琐的计算步骤。SymPy还提供了可视化工具,使我们能够以图形方式展示数学结果,从而更好地理解和分析问题。
总而言之,SymPy是一个功能强大的符号计算库,为数学和科学计算提供了便捷的工具。它的灵活性和可扩展性使得用户能够根据自己的需求进行定制和扩展。通过使用SymPy,我们能够更高效地进行数学计算和建模,推动科学研究和工程应用的发展。
文章来源:https://blog.csdn.net/weixin_41704077/article/details/135670904
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 使用好的GPU的优点
- Java中的List: 理解与实践
- 使用UTF-8编码处理多语言文本的有效策略
- 《ARM Linux内核源码剖析》读书笔记——0号进程(init_task)的创建时机
- null 和 undefined 的区别?
- 华为OD机试 - 字符串拼接(Java & JS & Python & C)
- 深度学习基础知识整理
- 【PyQt学习篇 · ?】:QTableView的使用
- 大数据---33.HBase数据结构
- Python | 机器学习之数据清洗