统计学-R语言-5.2

---

前言

本篇文章将继续上篇的进行介绍。

---

大数定理

大数定理大数定理”的另一种表达方式是“均值定理”，其含义是，随机变量X多个观察值的均值会随着观察值的增加越发趋近于总体的期望值，中心极限定理进一步告诉我们，均值服从期望为μ 的正态分布。在各种测量试验中，我们一般都认为，测量结果的均值服从正态分布，根据总体均值估计的结论，正态分布的期望是应与观察值的均值近似相等。

中心极限定理是与大数定理并列的重要概率理论，它有几种不同的表达方式，核心思想是，大量的独立随机变量相加，不论各个随机变量的分布是怎样的，它们的加和必定会趋向于正态分布。

大数定理
在抛硬币的例子里，有一个重要的前提条件——硬币的正面与反面出现的概率各为50%。你觉得这看起来一定是对的吗？科学不相信感觉，科学相信实验。

  下面，请准备好一枚一角的硬币（因为一角的更轻），咱们一起来做抛硬币的实验。实验过程是：高高抛起硬币并接住，每抛一次，都把结果记录下来，正面的次数X和反面的次数Y分别记录。

抛到10次，结果是，正面3次，反面7次。
抛到100次时，结果是，正面43次，反面57次。
抛到200次时，结果是，正面97次，反面103次。
抛到1000次时，结果是，正面513次，反面487次。

这个实验可以永远进行下去，实验的目的不是找到某一次抛掷，使得X和Y刚好相等，实验的目的是观察X和Y的变化趋势。因此，实验暂时只进行到1000次。下图是根据抛掷过程绘制出的曲线，曲线代表的是正面所占的比例，即X/（X+Y）随抛掷次数的变化。

图中曲线呈现的特征是，当抛掷次数很少时正面所占比例的变化幅度很大，并且与0.5的差值比较大，随着抛掷次数越来越多，正面所占的比例的变化幅度越来越小，而且一直围绕在0.5的周围。根据这条曲线，我们甚至可以预期，1000次之后的曲线还会在0.5周围徘徊，感兴趣的同学可以把实验继续做下去。
大数定理，指的是随机事件发生的频率会随着随机试验次数的不断增加趋向于它的概率，简单来说就是，试验次数越多频率离概率越近，而且越稳定。在上面的实验中，随机事件是“抛硬币出现正面”，频率是“正面出现所占的比例X/（X+Y）”，随着抛掷次数的增加，这个频率越发趋近概率值0.5，大数定理像一只“看不见的手”，掌控着试验过程。

空手套利的庄家
我们回到赌场，坐回到赌桌前，看一看大数定理是怎么暗中帮助庄家赚到钱的。
我们要玩的是赌场里很流行的一个游戏-----大转盘。游戏的道具是如下图所示的大转盘，转盘上有38个格子，格子里填写了1~36的数字和两个特殊数字0、00，玩家的下注方式有很多种比如下注奇数，下注黑色格子的数字，或者下注某一个数字。这里需要特别说明的是，0和00这两个数字不包含在任何赌注中，这两个数字是留给庄家的，就是说，当转盘的指针最终指向0或00时，庄家赢得所有的筹码。

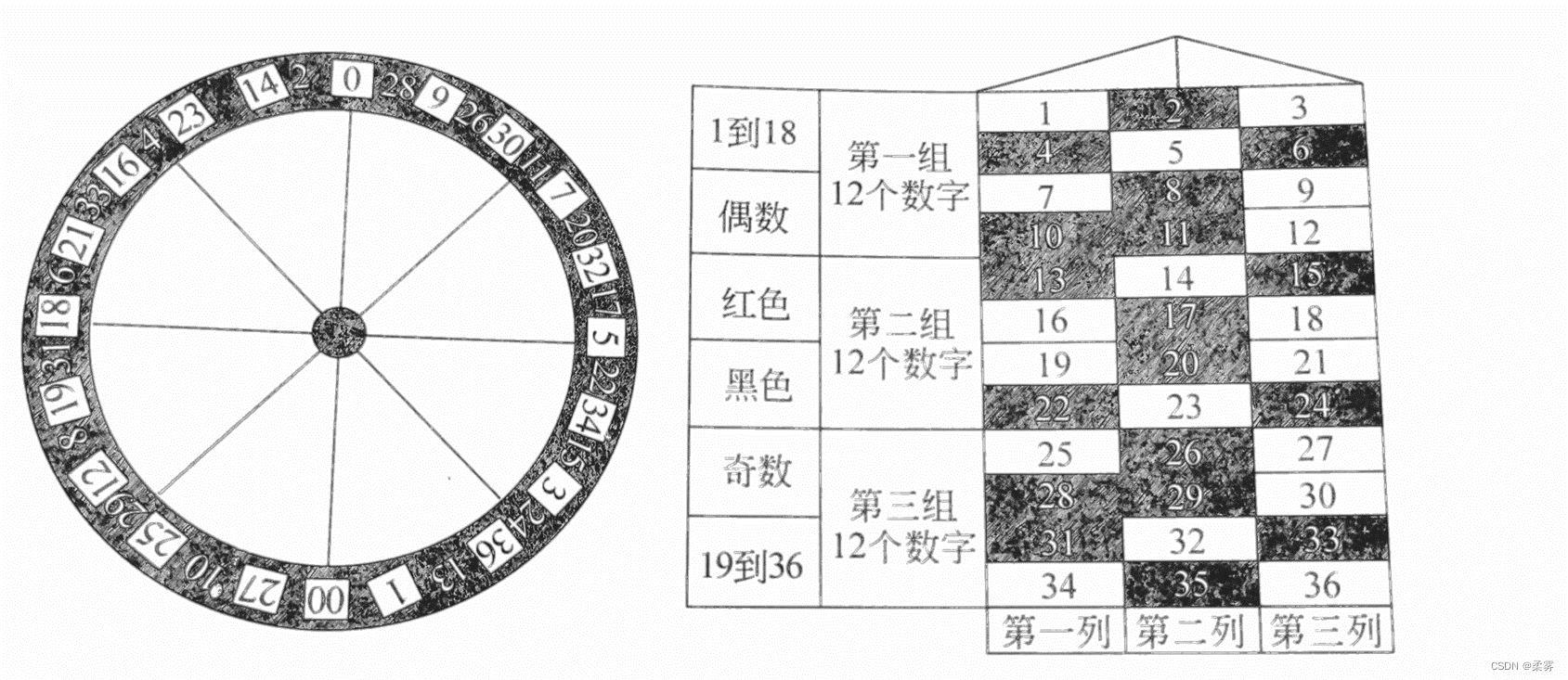
空手套利的庄家
我们挑选赢的概率最大和最小的两种赌注。
赢的概率最小的赌注是下注某一个数字，当玩家下注某一个数字时，他赢的概率是1/38，而此时庄家赢的概率是2/38，很显然，玩家会输给庄家！
赢得概率最大的赌注是下注黑色（或红色）数字，当玩家下注黑色（或红色）数字时，他赢的概率是18/38，这时，庄家赢的概率仍然是2/38，很显然，玩家会战胜庄家！
很显然，上面的分析是错的！
因为玩家和庄家要赢的是筹码，可不是概率！概率只是我们分析赌局的工具，玩家们真正关注的不是概率，而是所赢筹码的期望。为了计算所赢筹码的期望，我们首先要了解赌场里一个重要的常识——赔率。

赔率是赌场为每一个赌注设置的“赔钱比例”，比如，在2015—2016赛季英超联赛开始前，博彩公司为莱斯特城队开出的夺冠赔率是1：5000，这个比例的含义是，玩家用1英镑下注莱斯特城队夺冠，如果莱斯特城队最终夺冠，博彩公司会付给玩家5000英镑（含玩家下注的1英镑）。同时，阿森纳的夺冠赔率是1：3.5，即，下注阿森纳夺冠1英镑的玩家，即使赢了也只能得到3.5英镑。从这样的赔率可以看出，在英超联赛开始之前，博彩公司看好阿森纳夺冠，看衰莱斯特城队夺冠，这就是赔率的含义。

下表给出了大转盘中各类赌注的赔率，我们利用这些赔率来计算玩家和庄家所赢筹码的期望。

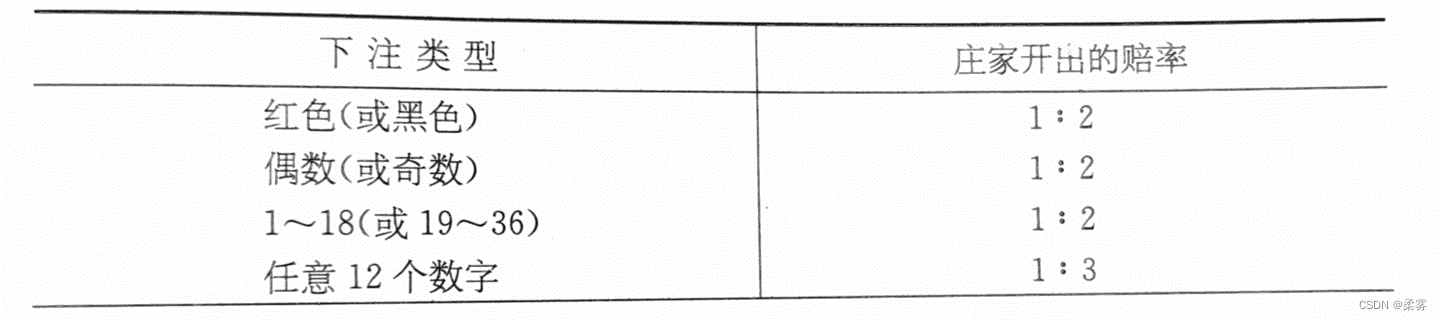
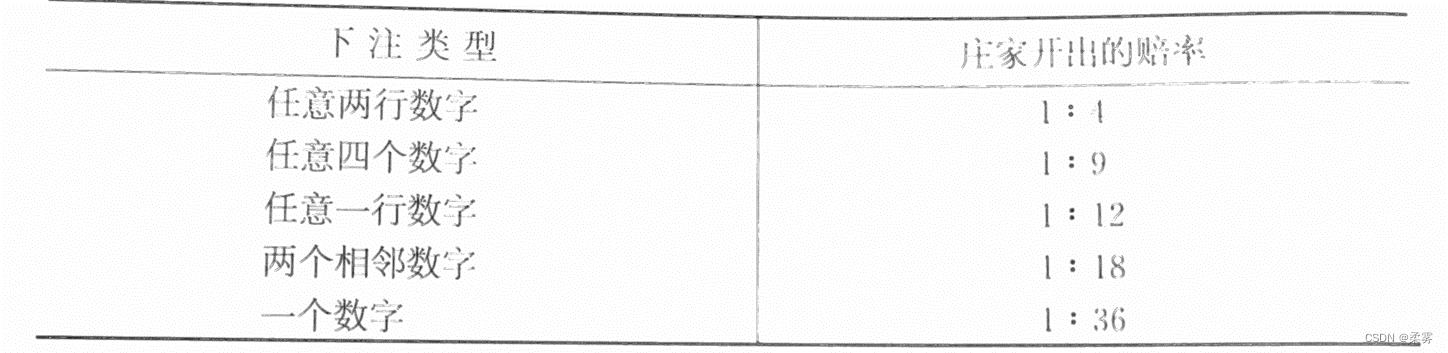
假设玩家拿一个筹码下注某一个数字，他赢的概率是1/38，赢了可以得到35个筹码，输的概率是37/38，输了会输掉这一个筹码，所以玩家所赢筹码的期望是：
E（玩家下注某个数字时，玩家所赢筹码）=1/38×35+37/38×（-1）= -1/19= -0.0526
与玩家相对的，庄家所赢筹码的期望是：
E（玩家下注某个数字时，庄家所赢筹码）=1/38×（-35）+37/38×(+1)= 1/19=0.0526
用同样的方法，可以计算出玩家下注黑色数字时玩家和庄家所贏筹码的期望：
E（玩家下注黑色数字时，玩家所赢筹码）=18/38×(+1)+20/38×（-1）= -1/19= -0.0526
E（玩家下注黑色数字时，庄家所赢筹码）=18/38（-1）+20/38×（+1）= 1/19=0.0526

事实上，不论何种赌注，玩家所赢筹码的期望都是-0.0526，庄家所赢筹码的期望都是0.0526，同学们可以选择其他类型的赌注自行验证。
至此，我们终于看清了大转盘的本来面目，它是一个典型的“零和博弈”， 庄家赢的筹码等于玩家输掉的筹码，平均意义上看，玩家每下注1个筹码，就会输掉0.0526个筹码，同时庄家会赢得0.0526个筹码。0.0526看起来很微小，这正是庄家想要的效果，玩家就像温水中的青蛙，沉浸在赌局中，却不知自己的钱正在像沙漏中的细沙一样，缓缓地流进了庄家的钱袋。
在这个赌局中，庄家要做到稳赚不赔，就要满足大数定理实现的条件：实验次数足够多。因此，庄家会想方设法地吸引玩家不停地玩下去，玩家越是沉迷于其中，庄家赚到的筹码也越多，这就是庄家空手套利的秘密。

中心极限定理和抽样分布

中心极限定理(central limit theorem,CLT)是概率论最重要的定理之一:
若给定样本量的所有样本来自任意总体，则样本均值的抽样分布近似服从正态分布，且样本量越大，近似性越强
中心极限定理指出，对于大容量的随机样本，其样本均值的抽样分布形态近似于一个正态概率分布。这是统计学中非常有用的结论之一
我们可以在对样本来源分布形态一无所知的情况下，推断样本均值的分布。

中心极限定理: 若给定样本量的所有样本来自任意总体，则样本均值的抽样分布近似服从正态分布，且样本量越大，近似性越强。

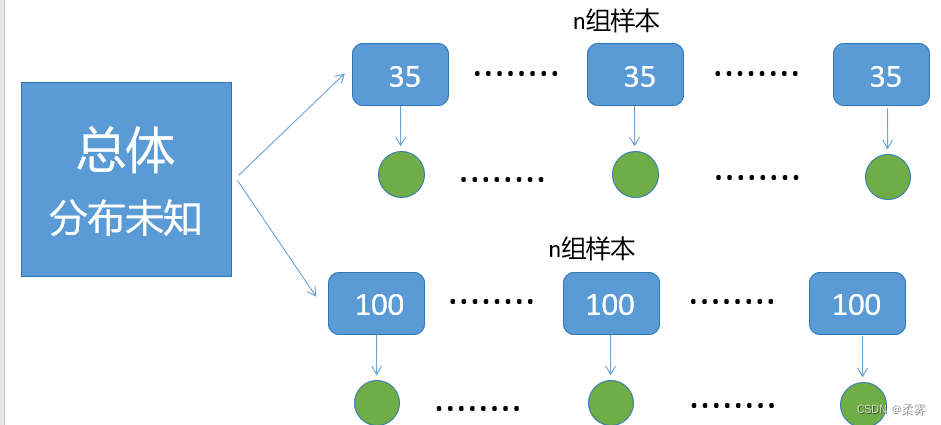
根据中心极限定理可知，样本均值作为随机变量有如下性质(注意，这里并没有假定X的分布):
(1)如果能够选择给定总体的特定容量的所有可能样本,那么,样本均值的抽样分布的均值将恰好等于总体均值,即 ,即使我们不能得到所有样本,但可以预计样本均值分布的均值会接近于总体均值。
(2)样本均值的抽样分布的离散程度小于总体分布。若总体标准差是σ,则样本均值x的抽样分布的标准差为 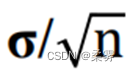。当样本量增大时, 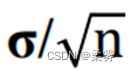值将变小,即x的集中程度变大。

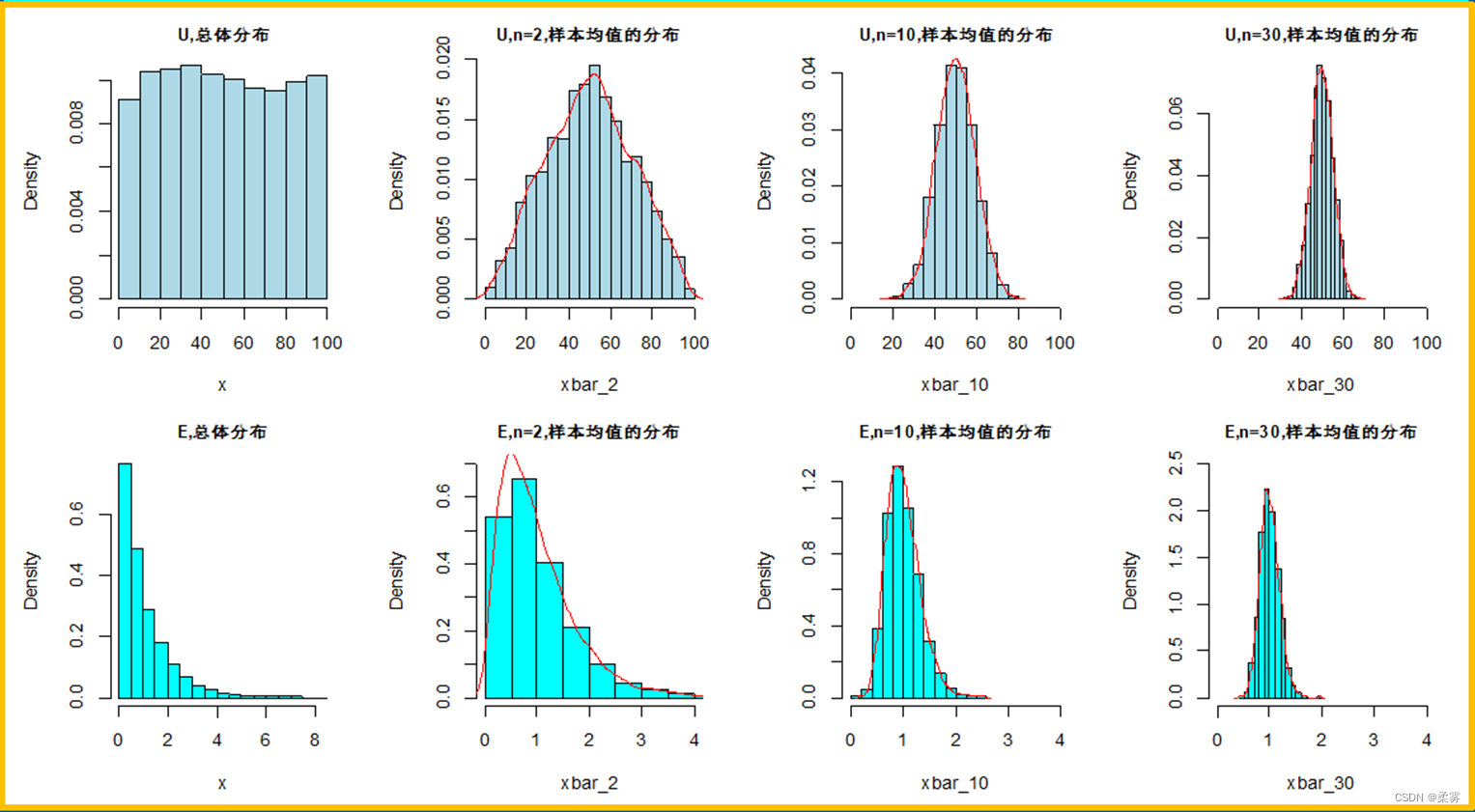
从0~100匀分布的总体和指数分布的总体中分别抽取样本量为2，10和30的各5000个样本，样本均值的分布如图所示。
随着样本量的增大，样本均值的分布逐渐趋于正态分布，而且分布越来越集中。

若把σ 换成样本标准差s, 得到的 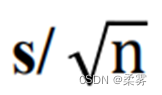就是均值的标准误(standard error of mean),它是对 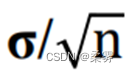的一个近似。
为什么样本均值的波动会比总体的波动小呢？这是由于样本是把N个数据取均值，而这N个数据里总是更可能有大有小，因而平均起来就会相互抵消，造成的结果就是波动范围变小。而且，N越大，这种相互之间的“拉平”作用越明显，从而波动（标准差）就减小得更多。
(3)即使X不是正态分布变量,在很一般的条件下,当样本量增加时,x的分布趋近于正态分布 。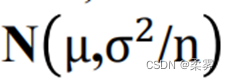

如果总体不是正态分布，当n为小样本（通常n<30）时，样本均值则不服从正态分布。
样本均值的分布与总体分布及样本量的关系如图所示：

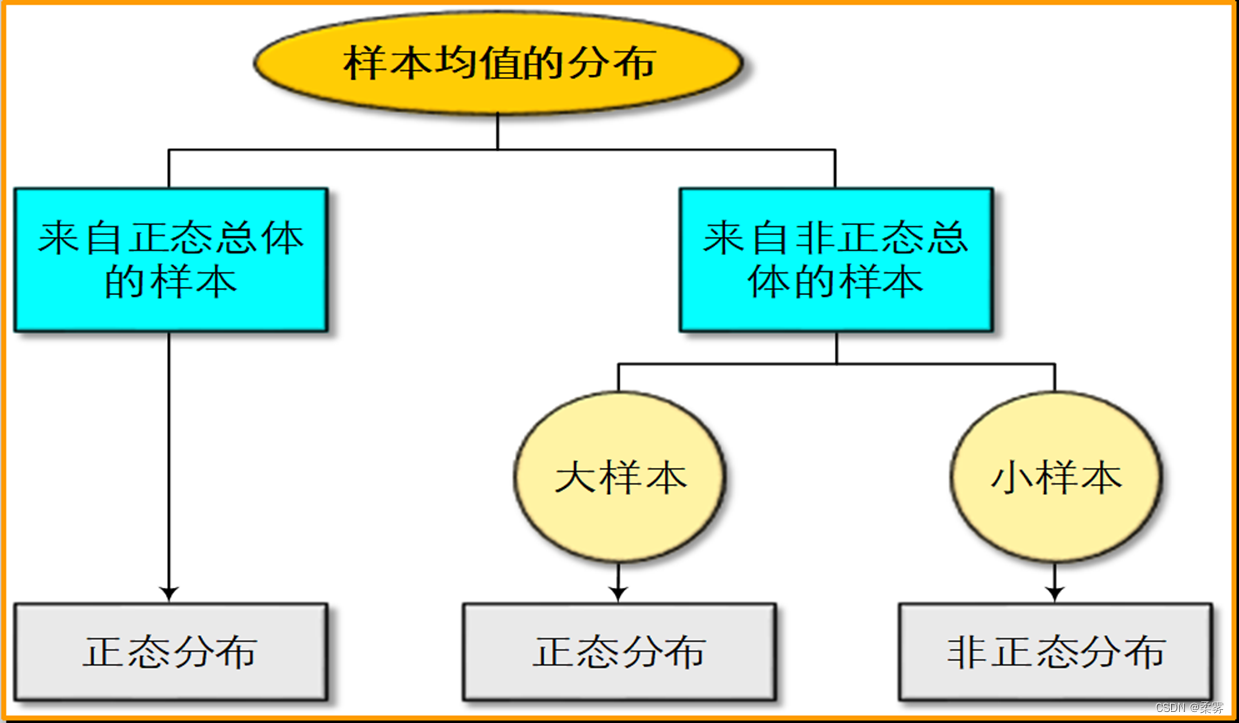
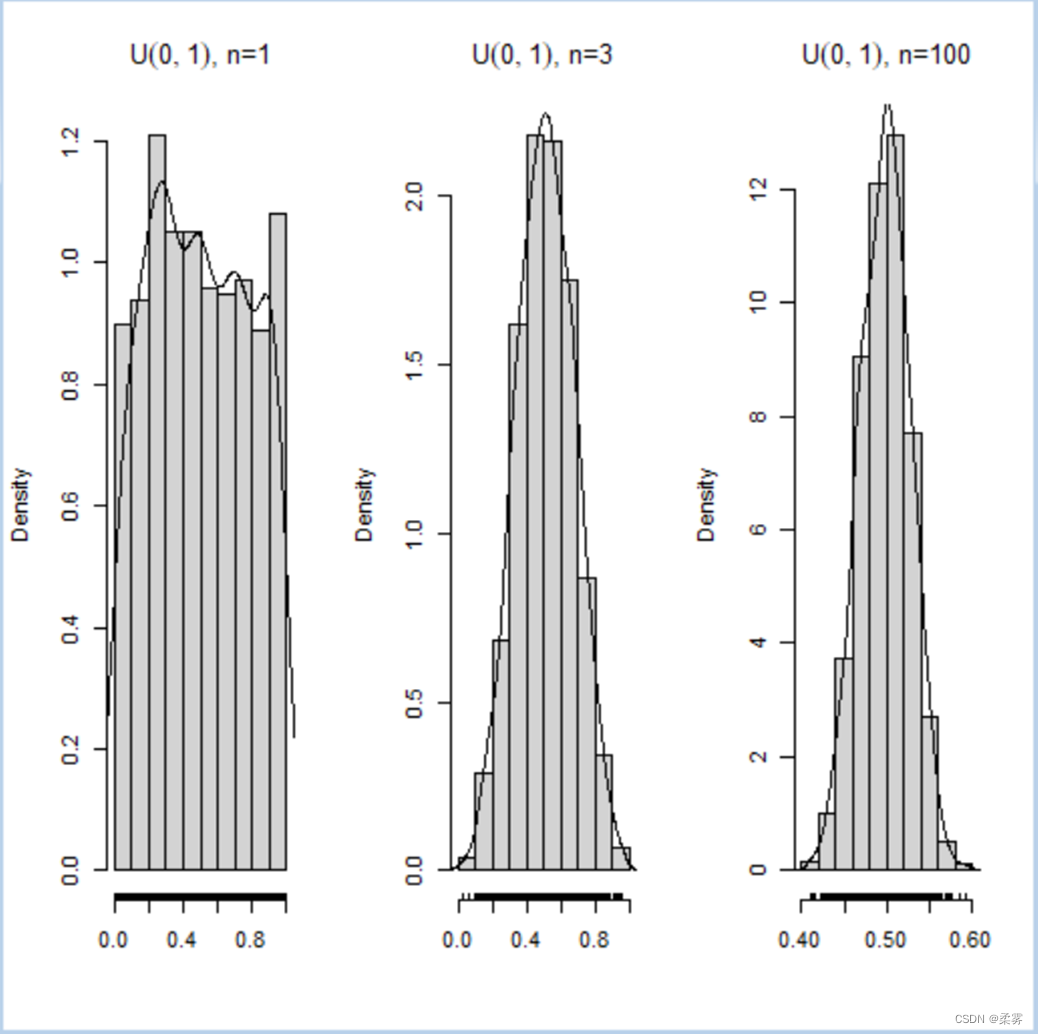
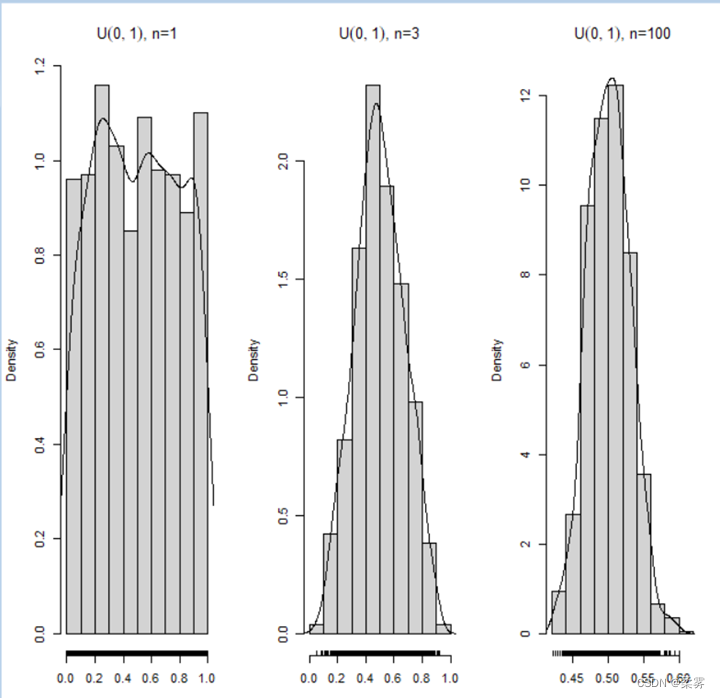
从U(0,1)分布对于三种样本量n=1, 3, 100分别取1000个样本,对每组样本算出均值。这样对每一种样本量都有1000个均值，用这些均值画直方图，见下图：

a=NULL;for(i in 1:1000)a=c(a,runif(1))#runif(x)产生x个随机数，for循环1000次，扩充a序列，生成1000个样本均值
b=NULL;for(i in 1:1000)b=c(b,mean(runif(3)))
c=NULL;for(i in 1:1000)c=c(c,mean(runif(100)))
unif=cbind(a,b,c);par(mfrow=c(1,3))#形成三列样本，分别对应a,b,c
hist(unif[,1],freq=F,xlab="",main=expression(paste(U(0,1),", n=1")))#对a样本列绘制直方图，freq: 逻辑值，默认值为TRUE , y轴显示的是每个区间内的频数，FALSE, 代表显示的是频率
lines(density(a));rug(a)

hist(unif[,2],freq=F,xlab="",main=expression(paste(U(0,1),", n=3")))
lines(density(b));rug(b)
hist(unif[,3],freq=F,xlab="",main=expression(paste(U(0,1),", n=100")))
lines(density(c));rug(c)

NULL表示空值，表示没有内容。一般常用在函数参数中，表示该参数没有被赋予任何值。也经常用在初始化变量，表示变量没有任何内容，因此它的长度为0。
c本身在这里是“combine”的首字母，用于合并一系列数字从而形成向量/数列。
cbind： 根据列进行合并，即叠加所有列，m列的矩阵与n列的矩阵,cbind()最后变成m+n列，合并前提：cbind(a, c)中矩阵a、c的行数必需相符。
paste函数把它的自变量连成一个字符串，中间用空格分开，如：

paste("Hello","world")

返回由空格连接的字符串。
[1] “Hello world”

在使用R语言作图时，有时需要在图上标注诸如求和、积分、上下标等数学符号，该操作可以通过expression函数完成。expression(…)
括号中输入数学表达式，配合plot、text、title、axis等函数使用，可以将数学公式绘制在图表上。
函数lines()用于在原图上添加直线或折线，命令为lines(x,y),其功能相当于plot(x,y,type=“1”)
rug(jitter(math)) #轴须图，在轴旁边出现一些小线段，jitter是加噪函数
density(a)原样本点对应的概率密度估计值。

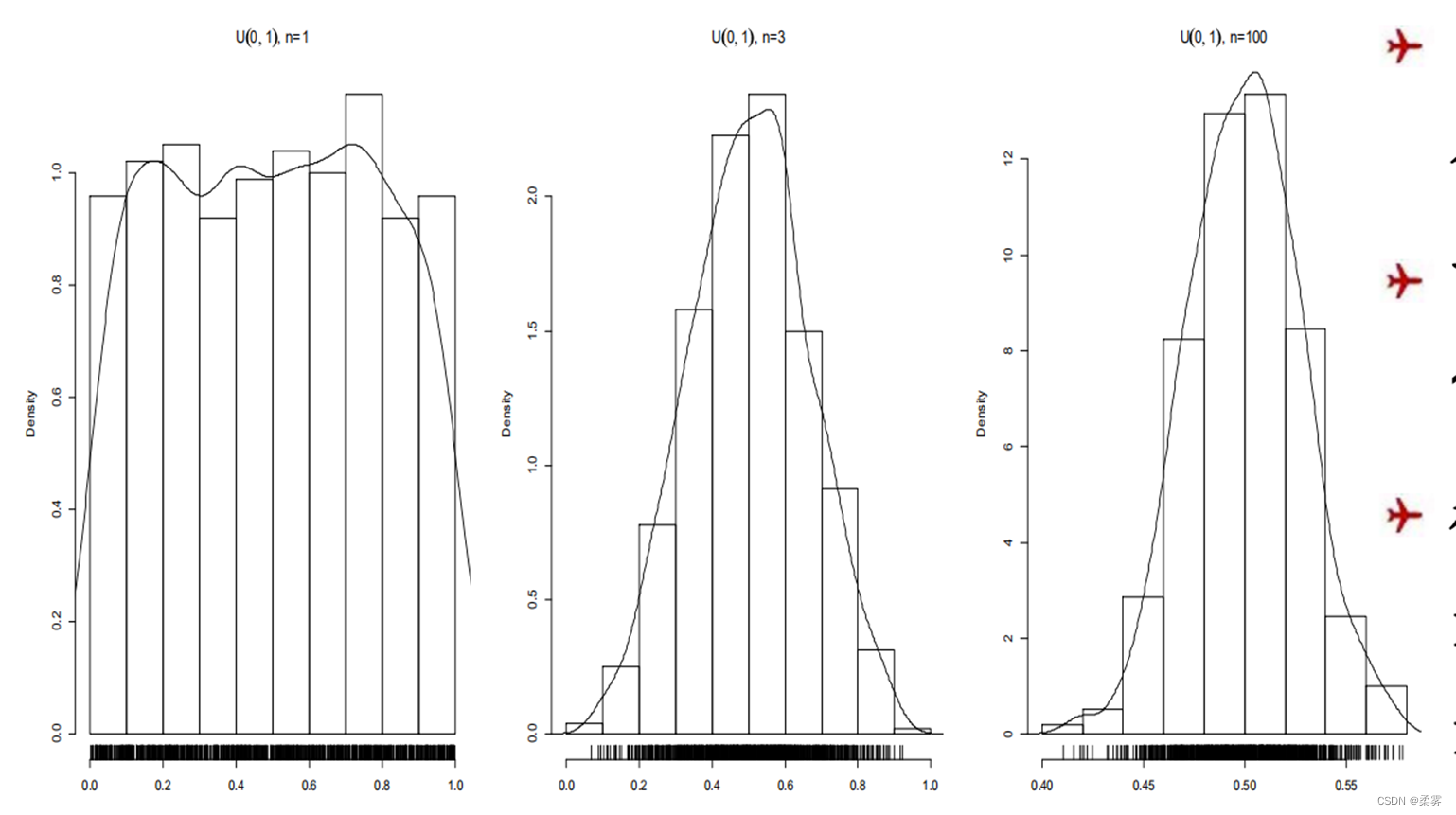
图中的曲线是对这1000个均值的密度估计。
下面小的短线标出了这1000个均值的实际位置。
可以看出，样本量越大，均值的直方图越像正态变量的直方图，而且数据的分散程度也越小,数据越集中。

在实际的抽样问题中，我们常常希望对总体进行评价，但往往又缺少总体信息。此时，中心极限定理就能发挥效力。假定总体均值和总体标准差σ都是未知的，而通常主要对总体均值感兴趣。
假定一个连续分布变量X的n个观测值组成一个样本，我们可以计算样本均值x和样本标准差s。可以用样本均值来估计μ的值，这种估计的好坏取决于样本均值的抽样分布。我们知道，对任何形态的总体分布，如果抽取一个容量足够大的样本，那么均值的抽样分布服从正态分布。样本均值的抽样分布将服从正态分布。统计理论证明，只要样本量大于30，就有理由相信均值的抽样分布服从正态分布。

抽样分布

可能关心某个地区所有家庭的平均收入是多少，但不可能去调查每个家庭的收入，而只能抽取一部分家庭作为样本，获得样本家庭的收入数据，然后用样本平均收入去推断全部家庭的平均收入。当然，也可能去推断所有家庭收入的方差是多少，低收入家庭的比例是多少，这就是抽样推断问题。那么，做出这种推断的依据是什么，这就必须知道用于推断的样本统计量是如何分布的（如样本均值 、样本比例p、样本方差 等）是如何分布的。

我们希望利用样本,特别是作为样本函数的样本统计量来了解总体,对总体参数进行推断
这些样本统计量包括前面提到过的样本均值、样本中位数、样本标准差以及由它们组成的函数
利用样本结果估计总体参数会产生抽样误差,那么,如何基于样本信息对我们感兴趣的目标进行估计或预测呢?为回答该问题,考察样本统计量的分布

相同样本量的样本统计量会随着样本的不同而不同
即样本统计量作为随机样本的函数,也是随机的, 也有自己的分布, 这些分布就称为抽样分布 (sampling distribution)

参数(parameter)
描述总体特征的概括性数字度量
一个总体的参数：总体均值(?)、标准差(?)、总体比例(?)；两个总体参数：(?1 -?2)、(?1-?2)、(?1/?2)
总体参数通常用希腊字母表示
统计量(statistic)
用来描述样本特征的概括性数字度量，它是根据样本数据计算出来的一些量，是样本的函数
一个总体参数推断时的统计量：样本均值(?x)、样本标准差(s)、样本比例§等；两个总体参数推断时的统计量： (?x1-?x2)、(p1-p2)、(s1/s2)
样本统计量通常用小写英文字母来表示

样本均值的分布

设总体共有N个元素（个体），从中抽取样本量为n的随机样本，在有放回抽样条件下，共有 个可能的样本，在无放回抽样条件下，共有 个可能的样本。
把所有可能的样本均值都计算出来，由这些样本均值形成的分布就是样本均值的概率分布，或称样本均值的抽样分布。但现实中不可能将所有的样本都抽出来，因此，样本均值的概率分布实际上是一种理论分布。当样本量较大时，统计证明它近似服从正态分布。下面通过一个例子说明样本均值的概率分布

例题如下：
（数据： example4_7. RData）设一个总体含有5个元素，取值分别为：
从该总体中采取重复抽样方法抽取样本量为n=2的所有可能样本，写出样本均值x的概率分布

分析： 取每一个值的概率都相同。总体的均值和方差分别为：

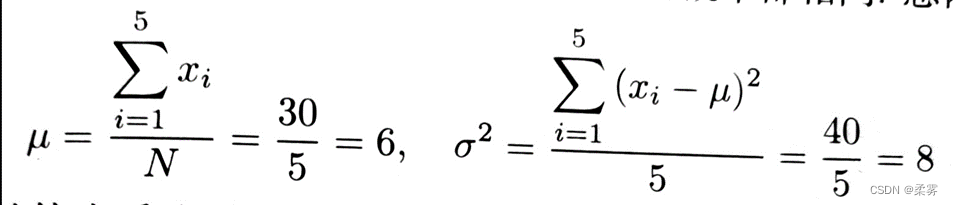
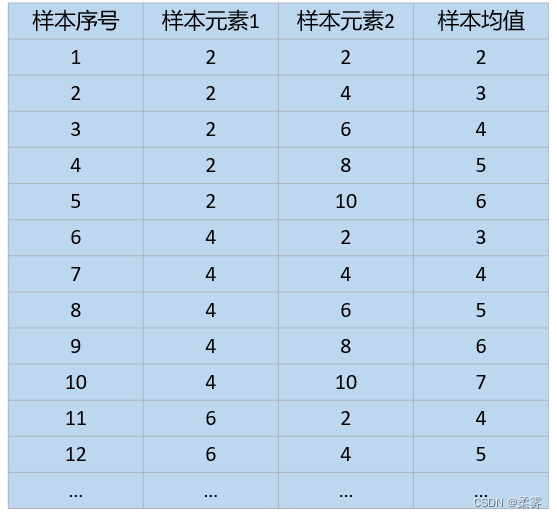
从该总体中采取重复抽样方法抽取样本量为n=2的随机样本，一共有25个可能的样本。
计算每一个样本的均值 ，如图所示：
样本均值的均值 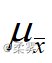，样本均值的方差 ：

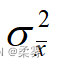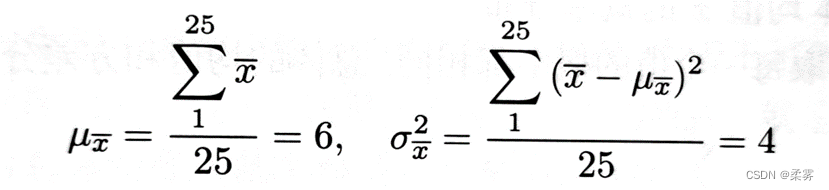
与总体均值μ，总体方差 进行比较：

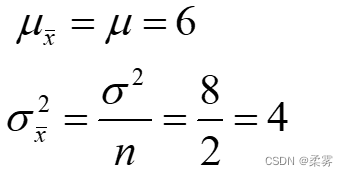
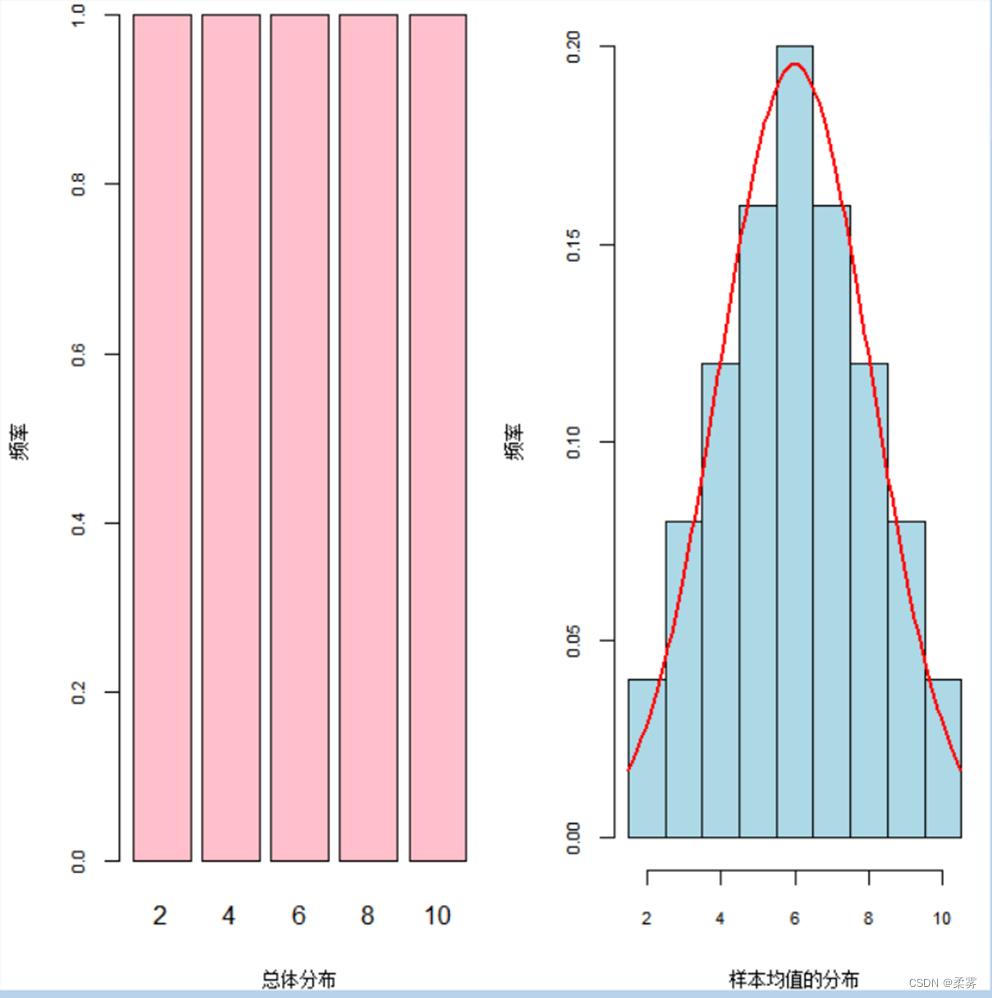
绘制总体分布与样本均值分布直方图R代码以及结果如下：

load("C:/example/ch4/example4_7.RData")
xx<-c(2,4,6,8,10)
par(mfrow=c(1,2),mai=c(0.8,0.8,0.1,0.1))
barplot(table(xx),xlab="总体分布",ylab="频率",cex.axis=0.7,cex.lab=0.7,col="pink")
hist(example4_7$样本均值,breaks=rep(1.5:10.5,by=2),ylab="频率",xlab="样本均值的分布",freq =FALSE,col="lightblue",cex.axis=0.7,cex.lab=0.7,main="")
curve(dnorm(x,mean(example4_7$样本均值),sd(example4_7$样本均值)),add=T,col="red",lwd=2)

样本均值的期望值和方差

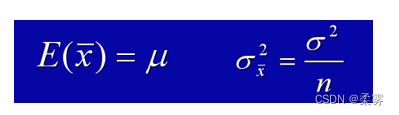
样本均值的分布

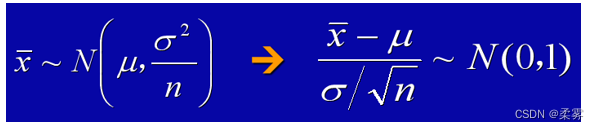
样本比例的分布

比例(proportion)：总体(或样本)中具有某种属性的个体与全部个体总数之比
不同性别的人与全部人数之比
合格品(或不合格品) 与全部产品总数之比
总体比例可表示为

样本比例可表示为

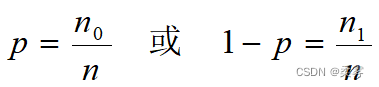
统计证明：当样本容量很大时，样本比例的抽样分布可用正态分布近似

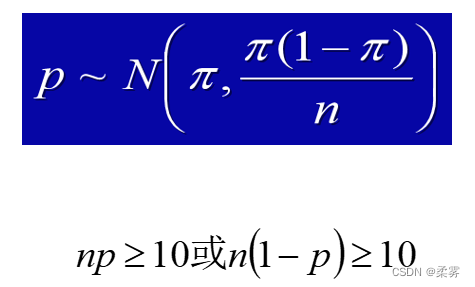
设总体比例π=0.2，从该总体中随机抽取样本量为50、100、500、1000的各5000个样本。模拟的样本比例的分布如图所示：
随着样本量的增大，趋于正态分布，分布越来越集中

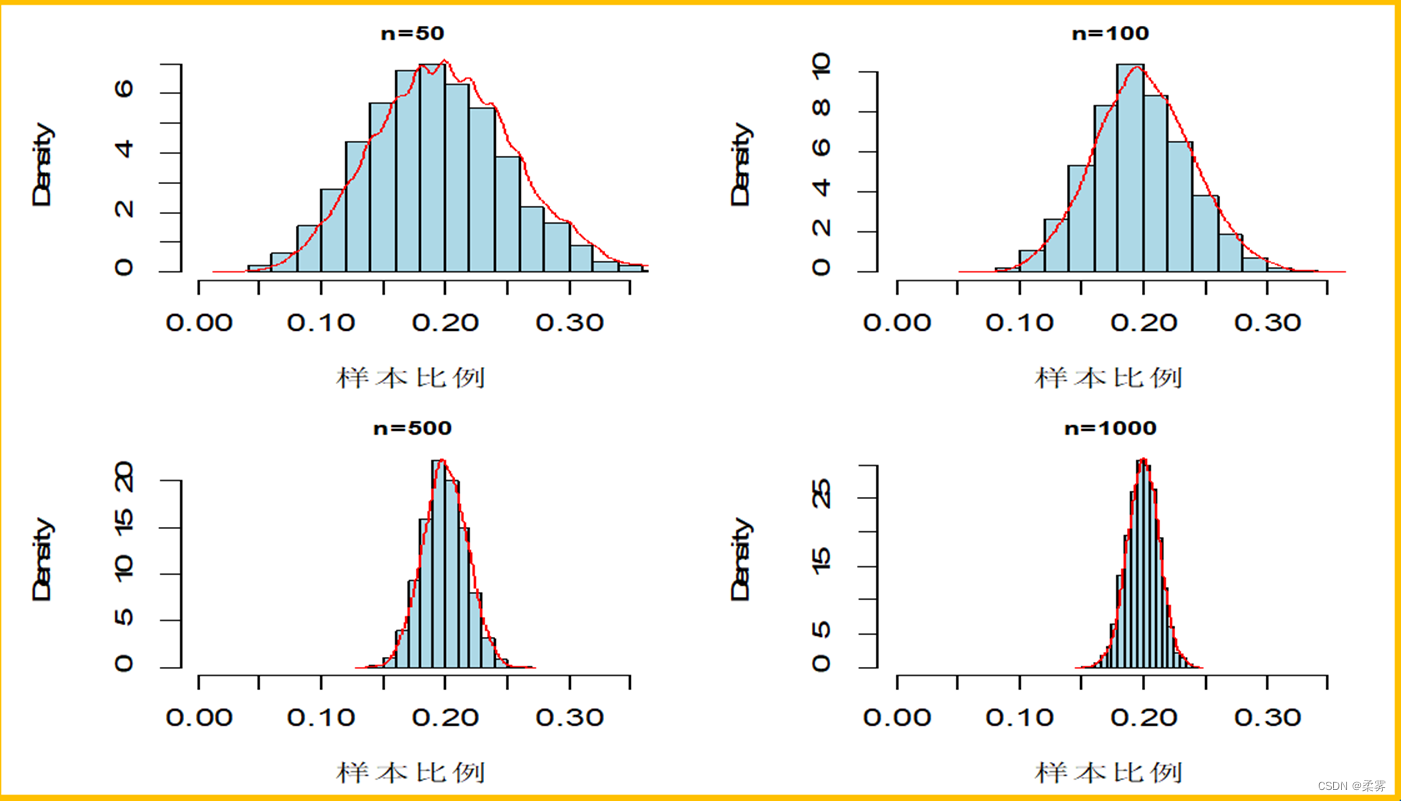
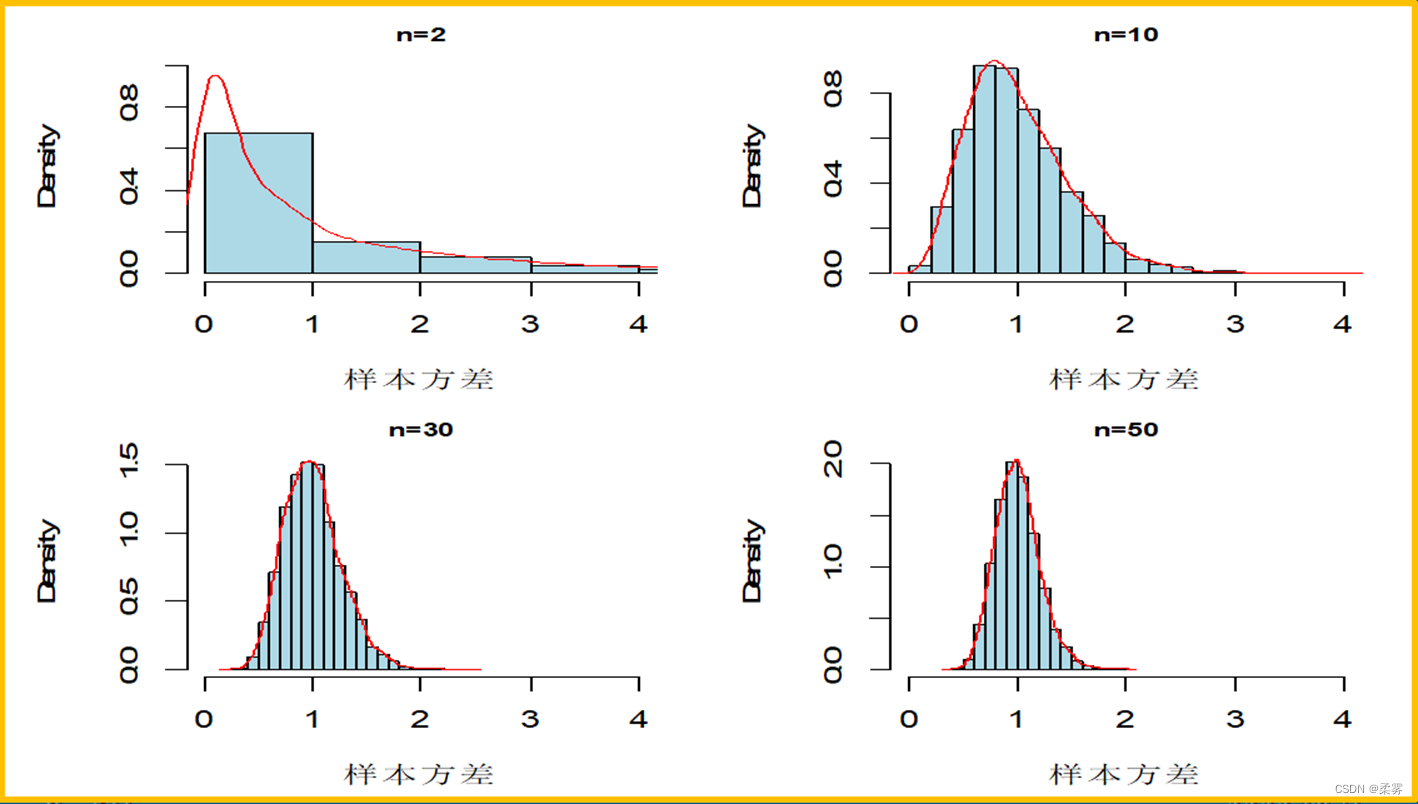
统计证明：对于来自正态总体的简单随机样本，则比值 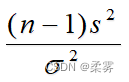的抽样分布服从自由度为 (n -1) 的x2分布，即

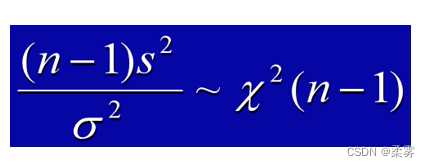
样本方差的分布形状与 ?2分布类似，随着样本量增大，逐渐趋于对称

---

练习

1、抽取不同的样本量模拟以下分布：
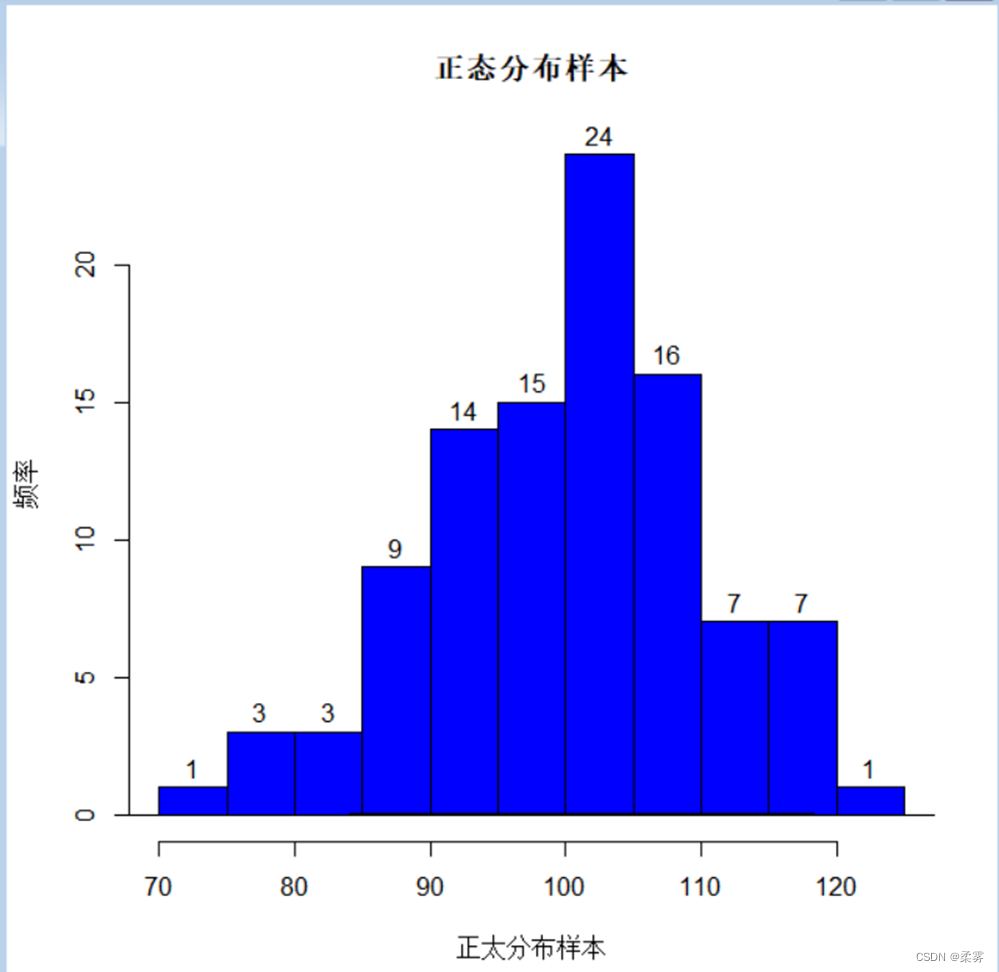
（1）正态分布，来自正态总体的样本

xx<-rnorm(5000,100,10)
x<-sample(xx,100,replace=T)#有放回
hist(x,ylab="频率",xlab="正太分布样本",labels=T,col="blue",main="正态分布样本")

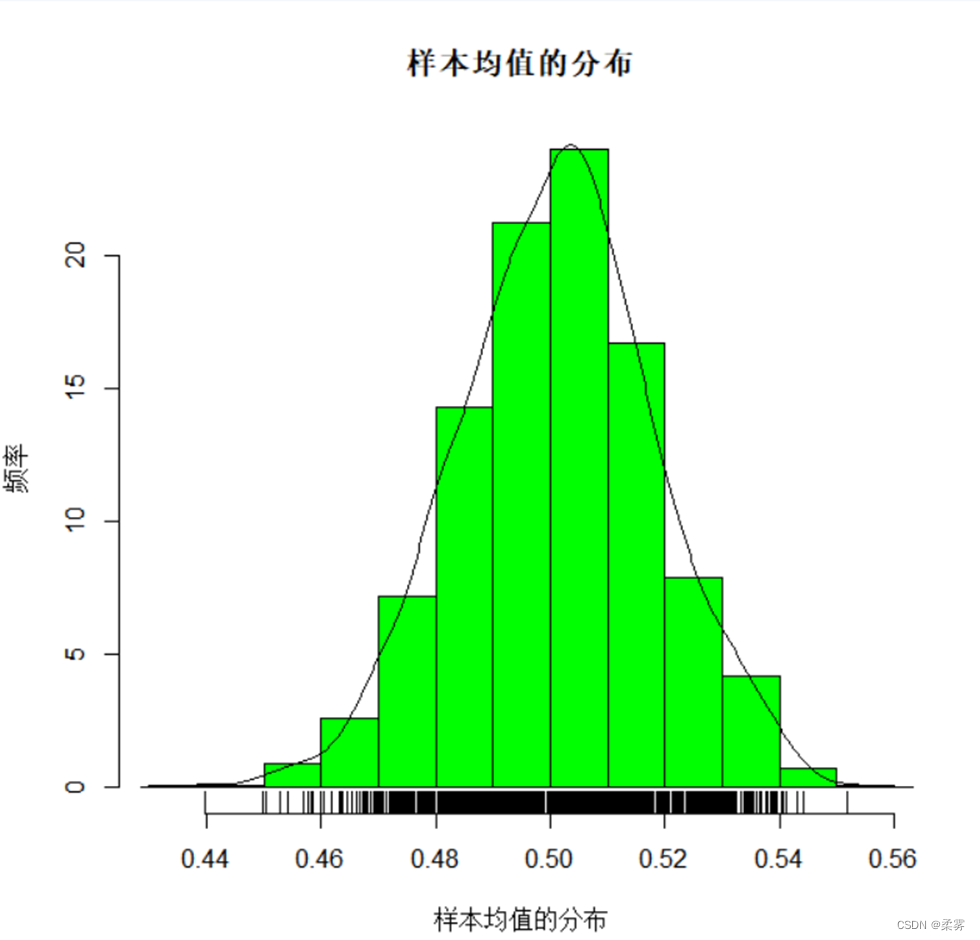
（2）样本均值的分布，来自任意总体的样本.

c=NULL;for(i in 1:1000)c=c(c,mean(runif(300)))
hist(c,freq=F,xlab="样本均值的分布",ylab="频率",col="green",main="样本均值的分布")
lines(density(c))
rug(c)

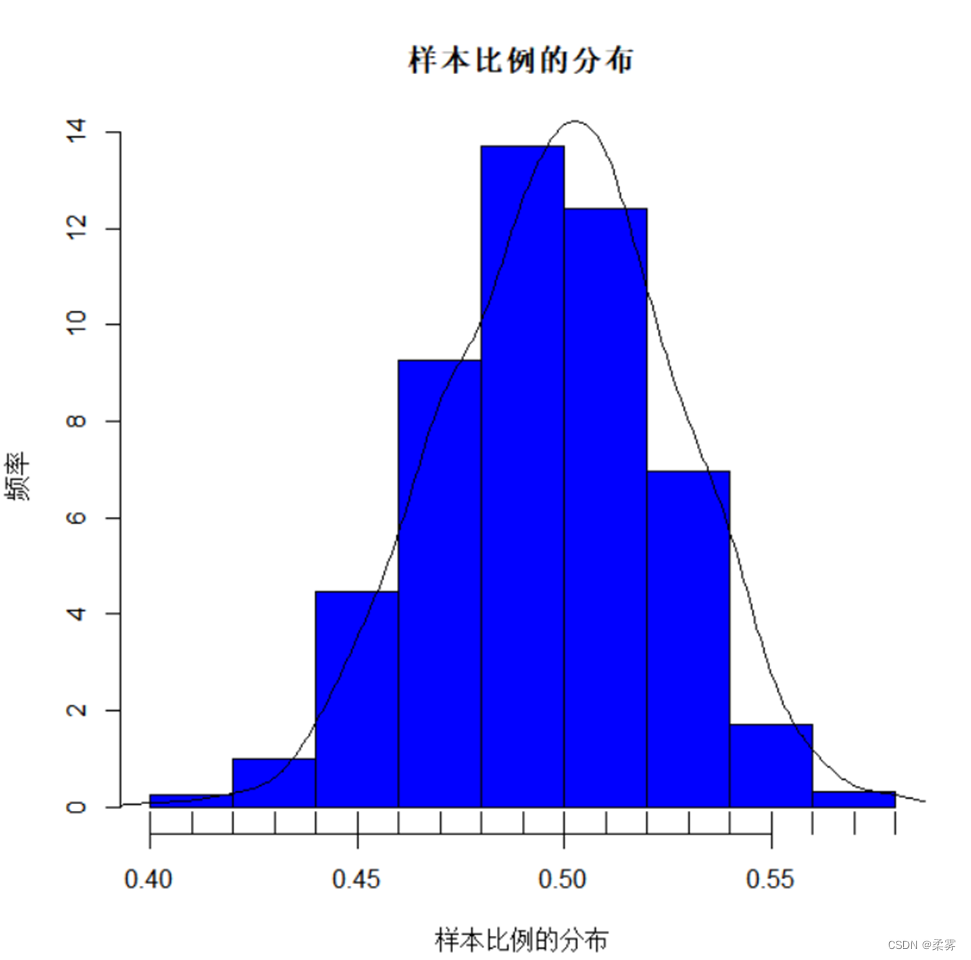
（3）样本比例的分布，来自任意总体的样本

d=NULL;for(i in 1:1000)d=c(d,round(length(which(rbinom(300,2,0.5)==1))/300,2))
hist(d,freq=F,xlab="样本比例的分布",ylab="频率",col="blue",main="样本比例的分布")
lines(density(d))
rug(d)

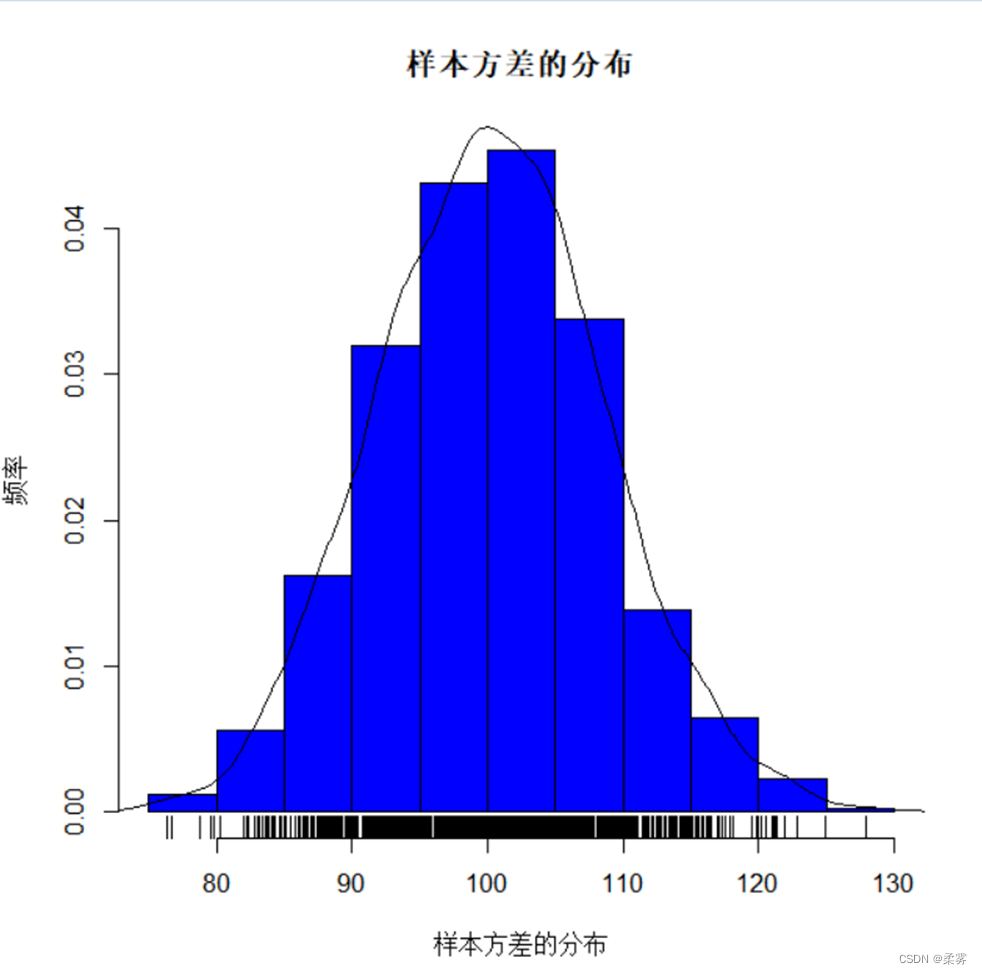
（4）样本方差的分布，来自正态总体的样本

e=NULL;for(i in 1:1000)e=c(e,var(rnorm(300,50,10)))
hist(e,freq=F,xlab="样本方差的分布",ylab="频率",col="blue",main="样本方差的分布")
lines(density(e))
rug(e)