leetcode 每日一题 2024年01月08日 回旋镖的数量
发布时间:2024年01月08日
题目
给定平面上 n 对 互不相同 的点 points ,其中 points[i] = [xi, yi] 。回旋镖 是由点 (i, j, k) 表示的元组 ,其中 i 和 j 之间的距离和 i 和 k 之间的欧式距离相等(需要考虑元组的顺序)。
返回平面上所有回旋镖的数量。
示例 1:
输入:points = [[0,0],[1,0],[2,0]]
输出:2
解释:两个回旋镖为 [[1,0],[0,0],[2,0]] 和 [[1,0],[2,0],[0,0]]
示例 2:
输入:points = [[1,1],[2,2],[3,3]]
输出:2
示例 3:
输入:points = [[1,1]]
输出:0
提示:
n == points.length1 <= n <= 500points[i].length == 2-10^4 <= xi, yi <= 10^4- 所有点都 互不相同
分析
-
回旋镖 是由点
(i, j, k)表示的元组 ,其中i和j之间的距离和i和k之间的欧式距离相等(需要考虑元组的顺序)。 -
欧式距离:
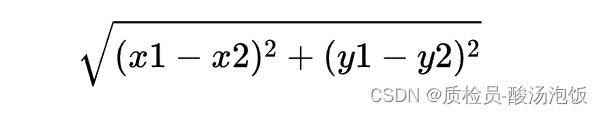
-
即我们需要以i为顶点,统计距离(dis)相等的顶点个数cnt,在从中选取2个(j,k),组成回旋镖,而且需要考虑顺序,即排列。
-
那么对于顶点i,回旋镖的数量为=从cnt中选2个的排列=
A(cnt,2)=cnt*(cnt-1) -
根据3的描述,数据结构可以使用map,key是dis,val是cnt
HashMap<Integer, Integer> disCount = new HashMap<>(); -
对于每个点都做顶点,循环计算回旋镖数量,再累计求和即可。
代码
会有一种情况,p1点和p2点是同一个点是,dis=0对应的以p1为顶点的点的个数是1
因为所有点都是互相不同的,所以双层for循环,dis=0,只会有一个点,不能构成回旋镖,可以不用理会,相当于ans+=0。
class Solution {
public int numberOfBoomerangs(int[][] points) {
int ans = 0;
//key是距离,value是距离相等的顶点个数
HashMap<Integer, Integer> disCount = new HashMap<>();
for (int[] point1 : points) {
disCount.clear();
for (int[] point2 : points) {
int dis = (point1[0] - point2[0]) * (point1[0] - point2[0]) + (point1[1] - point2[1]) * (point1[1] - point2[1]);
disCount.put(dis, disCount.getOrDefault(dis, 0) + 1);
}
for (Integer cnt : disCount.values()) {
ans += cnt * (cnt - 1);
}
}
return ans;
}
}
交流
qq群:
文章来源:https://blog.csdn.net/h88888888888/article/details/135453658
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Ubuntu中安装和配置SSH的完全指南
- (delphi11最新学习资料) Object Pascal 学习笔记---第2章第六节(类型转换)
- 『 C++ 』二叉树进阶OJ题
- 百亿西凤,站上新起点
- 【无标题】
- SpringBoot+Mybatis+MySQL+Vue实现CRUD+分页
- 【毕设选题指导】2024 数据分析与挖掘方向毕业设计选题推荐
- 父组件可以监听到子组件的生命周期吗
- (2023|AABI,多模态信息瓶颈,变分近似,视觉语言模型可解释性)通过多模态信息瓶颈归因对图像文本表示的视觉解释
- 文件属性stat