强化学习的数学原理学习笔记 - 蒙特卡洛方法（Monte Carlo）

---

参考资料：

1. 【强化学习的数学原理】课程：从零开始到透彻理解（完结）（主要）
2. Sutton & Barto Book: Reinforcement Learning: An Introduction
3. 机器学习笔记
4. GitHub - MathFoundationRL/Book-Mathmatical-Foundation-of-Reinforcement-Learning

本系列文章大部分内容来自西湖大学赵世钰老师的强化学习的数学原理课程（参考资料1），并参考了部分参考资料2、3的内容进行补充。

系列博文索引：（更新中）

• 强化学习的数学原理学习笔记 - RL基础知识
• 强化学习的数学原理学习笔记 - 基于模型（Model-based）
• 强化学习的数学原理学习笔记 - 蒙特卡洛方法（Monte Carlo）

*注：【】内文字为个人想法，不一定准确

概览：RL方法分类

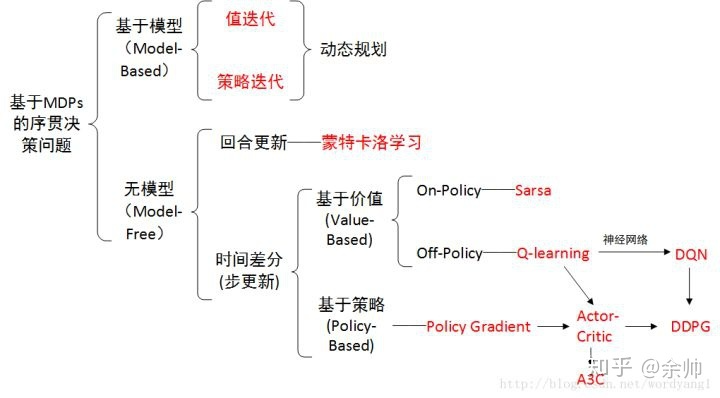
*图源：https://zhuanlan.zhihu.com/p/36494307

蒙特卡洛方法（Monte Carlo，MC）

求解RL问题，要么需要模型，要么需要数据。之前介绍了基于模型（model-based）的方法。然而在实际场景中，环境的模型（如状态转移函数）往往是未知的，这就需要用无模型（model-free）方法解决问题。

无模型的方法可以分为两大类：蒙特卡洛方法（Monte Carlo，MC）和时序差分学习（Temporal Difference，TD）。本文介绍蒙特卡洛方法。

蒙特卡洛思想：通过大数据量的样本采样来进行估计【本质上是大数定律的应用（基于独立同分布采样）】，将策略迭代中依赖于model的部分替换为model-free。

MC的核心idea：并非直接求解$q_{\pi }(s,a)$的准确值，而是基于数据（sample / experience）来估计$q_{\pi }(s,a)$的值。MC直接通过动作值的定义进行均值估计，即：
$$q_{\pi }(s,a)={\mathbb{E}}_{\pi }[G_t|S_t=s,A_t=a]\approx \frac{1}{N}\sum _{i=1}^N{g}^{(i)}(s,a)$$
其中$g^{(i)}(s,a)$表示对于$G_t$的第$i$个采样。

MC Basic

算法步骤：在第$k$次迭代中，给定策略${\pi }_k$（随机初始策略：${\pi }_0$）

• 策略评估：对每个状态-动作对$(s,a)$，运行无穷（或足够多）次episode，估算$q_{{\pi }_k}(s,a)$
• 策略提升：基于估算的$q_{{\pi }_k}(s,a)$，求解迭代策略${\pi }_{k+1}(s)={\mathrm{argmax}}_{\pi }{\sum }_a\pi (a|s)q_{{\pi }_k}(s,a)$

MC Basic与策略迭代的区别：在第$k$次迭代中

• 策略迭代使用迭代方法求出状态值$v_{{\pi }_k}$，并基于状态值求出动作值$q_{{\pi }_k}(s,a)$
• MC Basic直接基于采样/经验均值估计$q_{{\pi }_k}(s,a)$（不需要估计状态值）

*MC Basic只是用来说明MC的核心idea，并不会在实际中应用，因为其非常低效。

MC Exploring Starts

思想：提升MC Basic的效率

• 利用数据：对于一个轨迹，从后往前利用$(s,a)$状态-动作对采样做估计
  • 例如：对于轨迹$s_1\stackrel{a_2}{\to }{s}_2\stackrel{a_4}{\to }{s}_1\stackrel{a_2}{\to }{s}_2\stackrel{a_3}{\to }{s}_5\stackrel{a_1}{\to }?$，从后往前采样，即先估计$q_{\pi }(s_5,a_1)$，再估计$q_{\pi }(s_2,a_3)=R_{t+4}+\gamma q_{\pi }(s_5,a_1)$，进而估计$q_{\pi }(s_1,a_2)=R_{t+3}+\gamma q_{\pi }(s_2,a_3)$，以此类推
• 更新策略：不必等待所有episode的数据收集完毕，直接基于单个episode进行估计，类似于截断策略迭代（单次估计不准确，但快）
  • 这是通用策略迭代（Generalized Policy Iteration，GPI）的思想

MC Exploring Starts

• Exploring：探索每个$(s,a)$状态-动作对
• Starts：从每个状态-动作对开始一个episode
  • 与Visit对应：从其他的状态-动作对开始一个episode，但其轨迹能经过当前的状态-动作对

🟦MC ε-Greedy

Exploring Starts在实际中难以实现，考虑引入soft policy：随机（stochastic）选择动作

ε-Greedy策略：
$$\pi (a|s)=\{\begin{array}{ll}1?\frac{\epsilon }{|\mathcal{A}(s)|}(|\mathcal{A}(s)|?1),& \text{for?the?greedy?action,?}\\ \frac{\epsilon }{|\mathcal{A}(s)|},& \text{for?other?}|\mathcal{A}(s)|?1\text{?actions.}\end{array}$$
其中，$\epsilon \in [0,1]$，$|\mathcal{A}(s)|$表示状态$s$下的动作数量。

• 直观理解：以较高概率选择贪心动作（greedy action），以较低均等概率选择其他动作
• 特性：选择贪心动作的概率永远不低于选择其他动作的概率
• 目的：平衡exploitation（探索）和exploration（利用）
  • $\epsilon =0$：侧重于利用，永远选择贪心动作
  • $\epsilon =1$：侧重于探索，以均等概率选择所有动作（均匀分布）

MC ε-Greedy：在策略提升阶段，求解下式
$${\pi }_{k+1}(s)=\underset{\pi \in {\Pi }_{\epsilon }}{\mathrm{argmax}}\sum _a\pi (a|s)q_{{\pi }_k}(s,a)$$

其中，$\pi \in {\Pi }_{\epsilon }$表示所有ε-Greedy策略的集合。得到的最优策略为：
$${\pi }_{k+1}(a|s)=\{\begin{array}{ll}1?\frac{\epsilon }{|\mathcal{A}(s)|}(|\mathcal{A}(s)|?1),& a=a_k^{?},\\ \frac{\epsilon }{|\mathcal{A}(s)|},& a\ne a_k^{?}.\end{array}$$

MC ε-Greedy与MC Basic和MC Exploring Starts的区别：

• 后二者求解的范围是$\pi \in \Pi$，即所有策略的集合
• 后二者得到的是确定性策略，前者得到的是随机策略

MC ε-Greedy与MC Exploring Starts的唯一区别在于ε-Greedy策略，因此MC ε-Greedy不需要Exploring Starts。

MC ε-Greedy通过探索性牺牲了最优性，但可以通过设置一个较小的ε（如0.1）进行平衡

• 在实际中，可以为ε设置一个较大的初始值，随着迭代轮数逐渐减小其取值
• ε的值越大，最终策略的最优性越差

最终训练得到的策略，可以去掉ε，直接使用greedy的确定性策略（consistent）。