Single-Image Crowd Counting via Multi-Column Convolutional Neural Network

================================================================

论文背景

在2015年的上海大规模踩踏事件中，35人丧生。自那以后，世界各地发生了许多类似的人潮踩踏事件，导致更多的伤亡。因此，精确估算图像或视频中的人群数量对于计算机视觉技术在人群控制和公共安全方面的应用变得愈发重要。在公共集会、体育赛事等场景中，参与人数或密度是未来活动规划和空间设计的基本信息。良好的人群计数方法也可以扩展到其他领域，如从显微图像中计数细胞或细菌、在野生动物保护区估算动物群体的数量，或者估算交通枢纽或交通拥堵中的车辆数量等。

人群密度方法过去的发展历史

早期方法

以前的方法主要采用检测风格的框架，通过在视频序列的两个连续帧上扫描检测器，基于增强外观和运动特征，估算行人的数量。一些方法使用类似的基于检测的框架进行行人计数。然而，这些方法的局限性在于，它们通常假定人群由可以通过某些给定检测器检测到的单独实体组成，这在拥挤的环境或非常密集的人群中显着影响检测器性能和最终的估算准确性。

具体步骤如下
当我们想要数一群人的时候，可以通过观察视频中相邻两帧的变化来实现。方法是这样的：

• 看变化： 首先，我们会拿到视频中的两个连续画面，然后比较它们之间有哪些地方发生了变化，特别是有没有人在动。
• 找动的人： 如果有地方发生了变化，我们会认为那些是移动的个体，也就是人。这就是通过观察画面变化来找到人群的方法。
• 确认特征： 在找到的移动的地方，我们可能会再看一些其他特征，比如这些“移动的东西”是否看起来像人，或者它们的动作是不是像人的动作。
• 数人： 最后，通过统计在两个画面之间发现的“移动的东西”，我们就能大致估算视频中整个人群的数量。

基于轨迹聚类的方法

这种方法的核心思想是通过对视觉特征的轨迹进行聚类来计数人群。简单来说，就是通过观察视频中物体在一段时间内的运动轨迹，将相似的轨迹归为一类，从而估算人群的数量。但需要注意的是，这种方法适用于视频，而不适用于单个静止图像。

具体步骤如下

• 轨迹提取： 先从视频中提取物体的运动轨迹，可以使用一些跟踪器（比如KLT跟踪器）来追踪物体在不同帧之间的位置变化。
• 轨迹聚类： 将这些轨迹按照它们的相似度进行聚类，相似的轨迹被归为同一类。这里的相似度可能包括轨迹的形状、长度、速度等方面的特征。
• 估算人数： 每个聚类代表了一组相似运动的物体，我们可以认为这是同一群人。通过统计不同聚类中的轨迹数，就能估算出人群的数量。

基于特征回归的方法

这种方法通过对图像的前景进行分割，提取各种特征，然后使用回归函数来估算人群的数量。

具体步骤如下

• 分割前景： 在图像中，人群通常是前景，而其他部分是背景。首先，需要对图像进行前景分割，将人群从背景中分离出来。这可以使用图像分割算法来实现。
• 提取特征： 从前景图中提取各种特征，这些特征可以包括人群区域的面积、边缘数量、纹理特征等。这些特征将用作回归模型的输入。
• 回归函数： 使用回归函数来建模特征与人群数量之间的关系。回归函数的选择可以是简单的线性或分段线性函数，也可以采用更复杂的模型，如岭回归、高斯过程回归或神经网络。回归函数的目标是找到一个映射，使得输入特征可以准确地预测人群的数量。

具体的计算公式如下（以线性回归为例）

给定特征向量$x$（包括面积、边缘数量、纹理等），人群数量的估计$\hat{y}$为：
$$\hat{y}=w?x+b$$

其中，$w$是回归系数向量，$b$是偏置。通过训练回归模型，得到最优的$w$和$b$参数，使得预测值$\hat{y}$接近实际的人群数量。

这种方法的优势在于简单且易于理解，而更复杂的模型可以处理更高度非线性的关系，提高估算的准确性。

基于图像的方法

一些研究专注于从静态图像中估算人群数量。不同于前面介绍的视频帧间运动或轨迹聚类方法，这些方法主要依赖于单个静态图像。以下是其中一些方法的原理：

• 多信息源计数： 一种方法是利用单个图像中的多个信息源来计算密集群中的个体数量。这些信息源可以包括SIFT（尺度不变特征变换）、傅立叶分析、小波分解、GLCM（灰度共生矩阵）特征以及对头部的低置信度检测。通过综合利用这些信息，可以更全面地估算人群数量。
• 特征融合和支持向量机（SVM）： 另一种方法是利用预训练的卷积神经网络（CNN）提取图像特征，并将这些特征用于训练支持向量机（SVM）。具体而言，研究者可以使用多个信息源，如SIFT、傅立叶分析、小波分解、GLCM特征以及低置信度头部检测，将它们融合为一个综合的特征向量。然后，这个特征向量可以用于训练SVM，从而建立图像特征与人群数量之间的关系。

具体而言，特征融合可以表示为：

特征向量=[SIFT特征,傅立叶分析特征,小波分解特征,GLCM特征,低置信度头部检测特征,…]

然后，将这个特征向量用于训练SVM模型，该模型可以根据输入的图像特征向量来预测人群的数量。

这些方法的优势在于能够从静态图像中获取人群数量的信息，而不需要考虑视频帧之间的运动或轨迹信息。然而，对于不同的场景和图像，需要综合利用多个信息源，以提高估算的准确性。

Multi-column CNN用于人群计数

基于密度图的人群计数

在通过卷积神经网络（CNNs）估算给定图像中人数的过程中，有两种自然的配置。

• 一种是输入为图像，输出为估算的头部计数的网络。
• 另一种是输出人群的密度图（每平方米多少人），然后通过积分得出头部计数。

本文支持第二种选择，因为密度图保留更多信息。相对于总人群数量，密度图给出了图像中人群的空间分布信息，这在许多应用中都很有用。例如，如果某个区域的密度远高于其他区域，可能表明该区域发生了异常情况。

提出了使用CNN学习密度图的方法，其学习的滤波器更适应于不同大小头部，从而更适用于透视效应变化显著的任意输入。

通过几何自适应核生成密度图

由于CNN需要从输入图像训练以估算密度图，训练数据中给定的密度质量在很大程度上决定了方法的性能。

具体步骤

首先，对于图像中的每个头，将用一个$\delta$函数来表示。这个$\delta$函数在图像上的位置由$x_i$表示，其中$i$是头部的编号。如果图像中有$N$个头，那么将这些$\delta$函数的和表示为$H(x)$，其中$H(x)$是一个包含$N$个$\delta$函数的函数，即：

$$H(x)=\sum _{i=1}^N\delta (x?x_i)$$

为了将其转换为连续的密度函数，可以将该函数与高斯核$G_{\sigma }$卷积，使得密度为：
$$F(x)=H(x)?G_{\sigma }(x)$$

然而，这样的密度函数假定$x_i$是图像平面上的独立样本，而实际上，每个$x_i$是3D场景中地面上的人群密度样本，由于透视失真，与不同$x_i$对应的像素对应于场景中不同尺寸的区域。

为了准确估算人群密度$F$，需要考虑由地平面和图像平面之间的单应性引起的扭曲。然而，在任务和数据集中，通常并不知道场景的几何形状。尽管如此，如果假设每个头周围的人群在图像上是均匀分布的，那么头与其最近的$k$个邻居（在图像上）之间的平均距离给出了透视效应引起的几何扭曲的合理估计。

因此，应该基于图像中每个人的头尺寸自适应地确定传播参数$\sigma$。对于给定图像中的每个头$x_i$，将其到其$k$个最近邻居的距离表示为$[d_1^i,d_2^i,...,d_m^i]$。平均距离是${\bar{d}}^i=\frac{1}{m}{\sum }_{j=1}^m{d}_j^i$。

因此，与$x_i$关联的像素大致对应于场景中地面上半径与${\bar{d}}_i$成比例的区域。因此，为了估算$x_i$周围的人群密度，需要将$\delta (x?x_i)$与方差${\sigma }_i$成比例的高斯核卷积。更具体地说，密度$F$应为

$$F(x)=\sum _{i=1}^N\delta (x?x_i)?G_{\sigma }(x)$$，

其中${\sigma }_i=\beta ?{\bar{d}}_i$，$\beta$是参数。换句话说，我们使用自适应于每个数据点周围局部几何的密度核，称为几何自适应核。在实验中，我们经验性地发现$\beta =0.3$给出了最佳结果。

密度图估计的多列CNN

由于透视失真，图像通常包含不同大小的头，因此具有相同大小感受野的滤波器不太可能捕捉到不同尺度的人群密度特征。因此，更自然的方法是使用具有不同局部感受野大小的滤波器来学习原始像素到密度图的映射。受多列深度神经网络（MDNNs）成功的启发，提出使用多列卷积神经网络（MCNN）来学习目标密度图。在我们的MCNN中，对于每一列，我们使用不同大小的滤波器来建模与不同尺度头相对应的密度图。例如，具有较大感受野的滤波器对应于建模与较大头相对应的密度图。模型架构图如下：

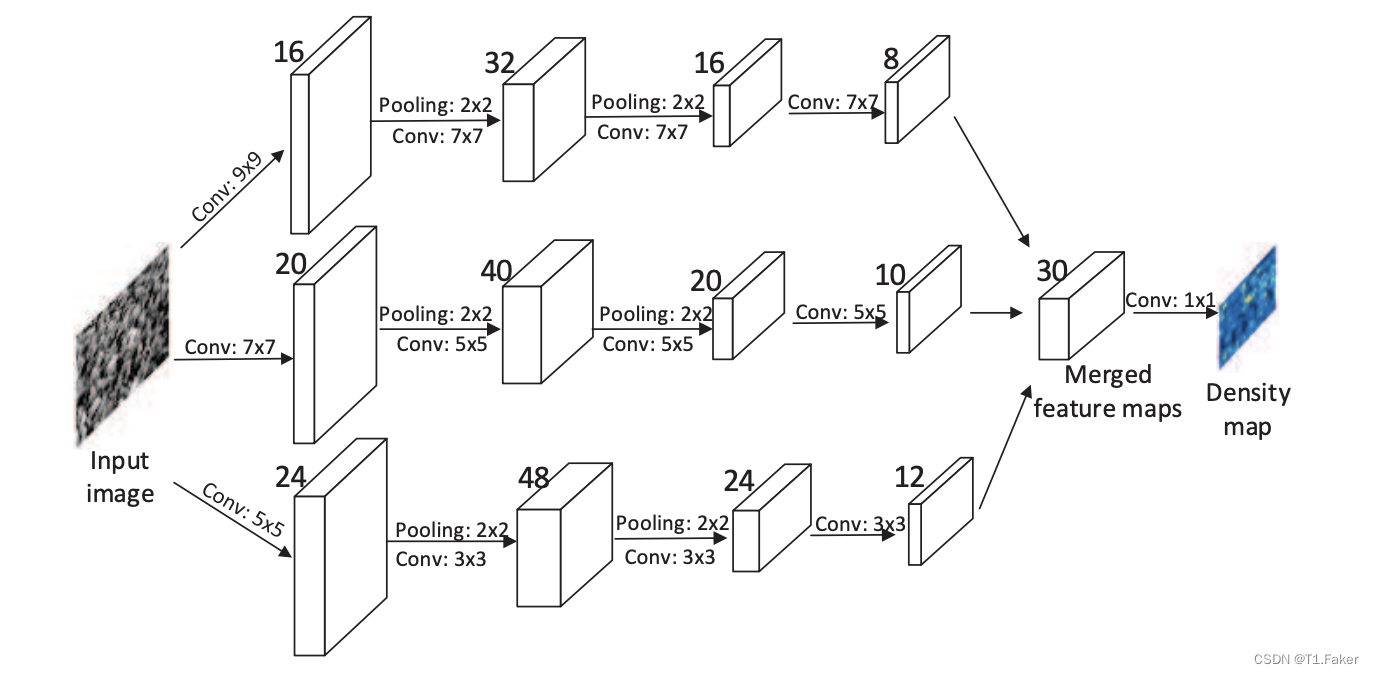
MCNN包含三个平行的CNN，其滤波器具有不同大小的局部感受野。为简化起见，我们对所有列使用相同的网络结构（即，conv–pooling–conv–pooling），除了滤波器的大小和数量。对于每个2×2区域，应用最大池化，并且由于ReLU对于CNN的性能良好，采用修正线性单元（ReLU）作为激活函数。

为了减少计算复杂性（要优化的参数数量），对具有较大滤波器的CNN使用较少的滤波器。堆叠所有CNN的输出特征图，并将它们映射到密度图。为了将特征图映射到密度图，采用滤波器大小为1×1。然后，使用欧几里得距离来衡量估算的密度图与地面实况之间的差异。损失函数定义如下：

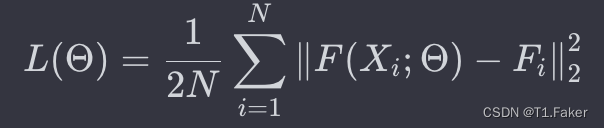
其中，$\Theta$是MCNN中可学习参数的集合，N是训练图像的数量，$X_i$是输入图像，$F_i$是图像$X_i$的地面实况密度图。$F(X_i;\Theta )$表示由带有参数$\Theta$的MCNN生成的估算密度图，$L$是估算密度图与地面实况密度图之间的损失。

注意事项：

• 由于使用两层最大池化，每个图像的空间分辨率减少了1/4。因此，在训练阶段，我们在生成密度图之前将每个训练样本下采样1/4。
• 传统的CNN通常将输入图像规范化为相同的大小。这里我们更喜欢输入图像保持其原始大小，因为将图像调整为相同的大小会引入难以估计的密度图中的额外失真。
• 除了CNN中的滤波器具有不同的大小之外，MCNN与传统MDNN之间的另一个区别是使用具有可学习权重的所有CNN的输出（即，1×1滤波器）进行组合。相比之下，在提出的MDNNs中，输出简单地平均。

骨干结构在计算机视觉模型中无论是图像分类目标检测或者人群计数等任务中起到了提取图像特征的作用。因此它骨干模型的内部输出图像其实就是一个类似的密度图，MCNN再结合多尺度就会把整个图片里所有人头都检测

我这里有一个实现骨干模型内部可视化的脚本可以参考，模型就用的最常见的骨干模型VGG，VGG模型代码在后面。

import torch
import torch.nn as nn
from torch.autograd import Variable
from torchvision.transforms import transforms
import numpy as np
import cv2
from functools import partial
import matplotlib
import os
import json
matplotlib.use('agg')
import matplotlib.pyplot as plt
import requests

from models import Vgg16Conv
from models import Vgg16Deconv

def load_and_preprocess_image(img_path):
    """加载和预处理图像"""

    # 从img_path读取图像
    img = cv2.imread(img_path)
    img = cv2.resize(img, (224, 224))

    # PyTorch必须通过以下均值和标准差对图片进行标准化
    transform = transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
    ])
    
    img = transform(img)
    img.unsqueeze_(0)
    return img


def hook_function(module, input, output, key):
    """用于存储特征图的钩子函数"""

    if isinstance(module, nn.MaxPool2d):
       model.feature_maps[key] = output[0]
       model.pool_locs[key] = output[1]
    else:
       model.feature_maps[key] = output


def register_hooks(model):
    """为骨干模型注册特征图存储钩子"""

    def hook(module, key):
        layer.register_forward_hook(partial(hook_function, key=key))

    for idx, layer in enumerate(model._modules.get('features')):    
        # _modules返回一个有序字典
        hook(layer, key=idx)


def visualize_layer(layer, vgg16_conv, vgg16_deconv):
    """可视化骨干模型的某一层的反卷积结果"""

    num_feat = vgg16_conv.feature_maps[layer].shape[1]
    
    # 将其他特征图激活设置为零
    new_feat_map = vgg16_conv.feature_maps[layer].clone()

    # 选择最大激活的特征图
    act_lst = []
    for i in range(0, num_feat):
        choose_map = new_feat_map[0, i, :, :]
        activation = torch.max(choose_map)
        act_lst.append(activation.item())

    act_lst = np.array(act_lst)
    mark = np.argmax(act_lst)

    choose_map = new_feat_map[0, mark, :, :]
    max_activation = torch.max(choose_map)
    
    # 对其他特征图进行零值处理
    if mark == 0:
        new_feat_map[:, 1:, :, :] = 0
    else:
        new_feat_map[:, :mark, :, :] = 0
        if mark != vgg16_conv.feature_maps[layer].shape[1] - 1:
            new_feat_map[:, mark + 1:, :, :] = 0
    
    choose_map = torch.where(choose_map==max_activation,
            choose_map,
            torch.zeros(choose_map.shape)
            )

    # 对其他激活进行零值处理
    new_feat_map[0, mark, :, :] = choose_map
    
    # 输出反卷积结果
    deconv_output = vgg16_deconv(new_feat_map, layer, mark, vgg16_conv.pool_locs)

    new_img = deconv_output.data.numpy()[0].transpose(1, 2, 0)  # (H, W, C)
    # 归一化
    new_img = (new_img - new_img.min()) / (new_img.max() - new_img.min()) * 255
    new_img = new_img.astype(np.uint8)
    return new_img, int(max_activation)


if __name__ == '__main__':
    
    img_path = './data/cat.jpg'

    # 前向处理
    img = load_and_preprocess_image(img_path)
    vgg16_conv = Vgg16Conv()
    vgg16_conv.eval()
    register_hooks(vgg16_conv)
    conv_output = vgg16_conv(img)
    pool_locs = vgg16_conv.pool_locs


    # 反向处理
    vgg16_deconv = Vgg16Deconv()
    vgg16_deconv.eval()
    plt.figure(num=None, figsize=(16, 12), dpi=80)
    plt.subplot(2, 4, 1)
    plt.title('Original Picture')
    img = cv2.imread(img_path)
    img = cv2.resize(img, (224, 224))
    plt.imshow(img)    
    for idx, layer in enumerate([14, 17, 19, 21, 24, 26, 28]):
    # for idx, layer in enumerate(vgg16_conv.conv_layer_indices):        
        plt.subplot(2, 4, idx+2)
        img, activation = visualize_layer(layer, vgg16_conv, vgg16_deconv)
        plt.title(f'{layer} Layer, Max Activation: {activation}')
        plt.imshow(img)

    plt.savefig('result.jpg')
    print('Result picture has been saved at ./result.jpg')

model.vgg16_conv.py

import torch
import torch.nn as nn
import torchvision.models as models
import torchvision

from collections import OrderedDict

class Vgg16Conv(nn.Module):
    """
    vgg16 convolution network architecture
    """

    def __init__(self, num_cls=1000):
        """
        Input
            number of class, default is 1k.
        """
        super(Vgg16Conv, self).__init__()
    
        self.features = nn.Sequential(
            # conv1
            nn.Conv2d(3, 64, 3, padding=1),
            nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1),
            nn.ReLU(),
            nn.MaxPool2d(2, stride=2, return_indices=True),
            
            # conv2
            nn.Conv2d(64, 128, 3, padding=1),
            nn.ReLU(),
            nn.Conv2d(128, 128, 3, padding=1),
            nn.ReLU(),
            nn.MaxPool2d(2, stride=2, return_indices=True),

            # conv3
            nn.Conv2d(128, 256, 3, padding=1),
            nn.ReLU(),
            nn.Conv2d(256, 256, 3, padding=1),
            nn.ReLU(),
            nn.Conv2d(256, 256, 3, padding=1),
            nn.ReLU(),
            nn.MaxPool2d(2, stride=2, return_indices=True),

            # conv4
            nn.Conv2d(256, 512, 3, padding=1),
            nn.ReLU(),
            nn.Conv2d(512, 512, 3, padding=1),
            nn.ReLU(),
            nn.Conv2d(512, 512, 3, padding=1),
            nn.ReLU(),
            nn.MaxPool2d(2, stride=2, return_indices=True),

            # conv5
            nn.Conv2d(512, 512, 3, padding=1),
            nn.ReLU(),
            nn.Conv2d(512, 512, 3, padding=1),
            nn.ReLU(),
            nn.Conv2d(512, 512, 3, padding=1),
            nn.ReLU(),
            nn.MaxPool2d(2, stride=2, return_indices=True)
        )

        self.classifier = nn.Sequential(
            nn.Linear(512 * 7 * 7, 4096),
            nn.ReLU(),
            nn.Dropout(),
            nn.Linear(4096, 4096),
            nn.ReLU(),
            nn.Dropout(),
            nn.Linear(4096, num_cls),
            nn.Softmax(dim=1)
        )

        # index of conv
        self.conv_layer_indices = [0, 2, 5, 7, 10, 12, 14, 17, 19, 21, 24, 26, 28]
        # feature maps
        self.feature_maps = OrderedDict()
        # switch
        self.pool_locs = OrderedDict()
        # initial weight
        self.init_weights()

    def init_weights(self):
        """
        initial weights from preptrained model by vgg16
        """
        vgg16_pretrained = models.vgg16(pretrained=True)
        # fine-tune Conv2d
        for idx, layer in enumerate(vgg16_pretrained.features):
            if isinstance(layer, nn.Conv2d):
                self.features[idx].weight.data = layer.weight.data
                self.features[idx].bias.data = layer.bias.data
        # fine-tune Linear
        for idx, layer in enumerate(vgg16_pretrained.classifier):
            if isinstance(layer, nn.Linear):
                self.classifier[idx].weight.data = layer.weight.data
                self.classifier[idx].bias.data = layer.bias.data
    
    def check(self):
        model = models.vgg16(pretrained=True)
        return model

    def forward(self, x):
        for idx, layer in enumerate(self.features):
            if isinstance(layer, nn.MaxPool2d):
                x, location = layer(x)
                # self.pool_locs[idx] = location
            else:
                x = layer(x)
        
        # reshape to (1, 512 * 7 * 7)
        x = x.view(x.size()[0], -1)
        output = self.classifier(x)
        return output

if __name__ == '__main__':
    model = models.vgg16(pretrained=True)
    print(model)

model.vgg16_deconv.py

import torch
import torch.nn as nn
import torchvision.models as models

import sys

class Vgg16Deconv(nn.Module):
    """
    vgg16 transpose convolution network architecture
    """
    def __init__(self):
        super(Vgg16Deconv, self).__init__()

        self.features = nn.Sequential(
            # deconv1
            nn.MaxUnpool2d(2, stride=2),
            nn.ReLU(),
            nn.ConvTranspose2d(512, 512, 3, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(512, 512, 3, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(512, 512, 3, padding=1),

            # deconv2
            nn.MaxUnpool2d(2, stride=2),
            nn.ReLU(),
            nn.ConvTranspose2d(512, 512, 3, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(512, 512, 3, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(512, 256, 3, padding=1),
            
            # deconv3
            nn.MaxUnpool2d(2, stride=2),
            nn.ReLU(),
            nn.ConvTranspose2d(256, 256, 3, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(256, 256, 3, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(256, 128, 3, padding=1),
            
            # deconv4
            nn.MaxUnpool2d(2, stride=2),
            nn.ReLU(),
            nn.ConvTranspose2d(128, 128, 3, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(128, 64, 3, padding=1),
            
            # deconv5
            nn.MaxUnpool2d(2, stride=2),
            nn.ReLU(),
            nn.ConvTranspose2d(64, 64, 3, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(64, 3, 3, padding=1)    
        )

        self.conv2deconv_indices = {
                0:30, 2:28, 5:25, 7:23,
                10:20, 12:18, 14:16, 17:13,
                19:11, 21:9, 24:6, 26:4, 28:2
                }

        self.unpool2pool_indices = {
                26:4, 21:9, 14:16, 7:23, 0:30
                }

        self.init_weight()

    def init_weight(self):
        vgg16_pretrained = models.vgg16(pretrained=True)
        for idx, layer in enumerate(vgg16_pretrained.features):
            if isinstance(layer, nn.Conv2d):
                self.features[self.conv2deconv_indices[idx]].weight.data = layer.weight.data
                #self.features[self.conv2deconv_indices[idx]].bias.data\
                # = layer.bias.data
        
    def forward(self, x, layer, activation_idx, pool_locs):
        if layer in self.conv2deconv_indices:
            start_idx = self.conv2deconv_indices[layer]
        else:
            raise ValueError('layer is not a conv feature map')

        for idx in range(start_idx, len(self.features)):
            if isinstance(self.features[idx], nn.MaxUnpool2d):
                x = self.features[idx]\
                (x, pool_locs[self.unpool2pool_indices[idx]])
            else:
                x = self.features[idx](x)
        return x

从上面图片来看，每层都有一些特征保留出来，而这种特征看起来像是一些opencv特征算法提取的感觉。这种特征结合高斯密度函数，就可以转为密度图啦