统计学-R语言-4.4

---

前言

上一篇文章介绍的是单变量数据，本篇将介绍双变量数据。

---

双变量数据

描述分类数据对分类数据的描述方法：二维表、复式条形图。
描述分类型数据对数值型数据的描述方法：箱线图。
描述数值型数据对数值型数据的描述方法：散点图、相关系数。

分类型数据对分类型数据–二维表

二维表（two-dimensional table）是两个变量进行交叉分类得到的频数表。
R的table()函数可以把双变量分类数据整理成 二维表形式
table()处理双变量数据类似处理单变量数据， 只是参数（变量）由原来的一个变成了两个。

例题1：
一份调查关于学生是否抽烟与每天学习时间关系的问题，具体数据如下表所示：

首先对数据进行编码：
是否抽烟设为变量smoke，其取值为Y和N分别表示抽烟和不抽烟
每天学习时间设为变量study， 其取值为< 5 h、5_{10h和>10h，分别表示少于5小时、5}10小时和超过10小时。
在R中输入数据：

smoke=c("Y","N","N","Y","N","Y","Y","Y","N","Y")
study=c("<5h","5~10h","5~10h",">10h",">10h","<5h","5~10h","<5h",">10h",  "5~10h")
table(smoke, study)
dw<-table(smoke,study)
dw

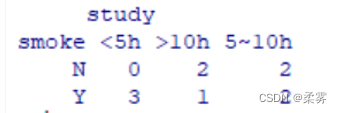
这就是是否抽烟与学习时间的二维表，列是学习时间的三个类型，行表示是否抽烟。

例题2：
生成被调查者所属社区与性别的列联表，为列联表生成边际和，并将列联表转化为百分比表，绘制二维列联表的R代码如下所示：

load("C:/example/ch2/example2_1.RData")
mytable1<-table(example2_1$社区,example2_1$性别)#制作出社区与性别的二维列联表
addmargins(mytable1)#为列联表生成边际和，addmargins()为表格加上边际和
addmargins(prop.table(mytable1))*100#为表格加上边际百分比

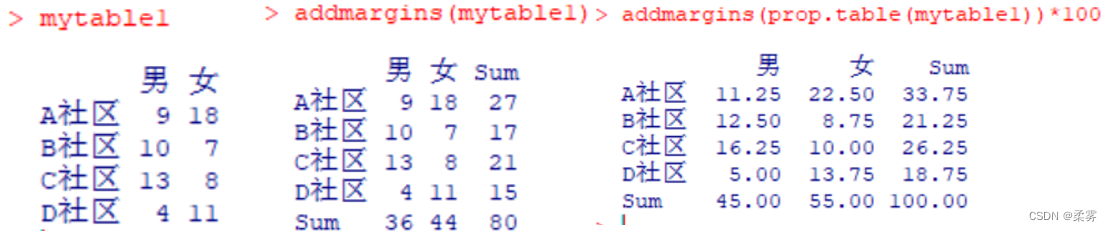
对于二维表，经常要计算某个数据占行、列汇总数的比例或是占总和的比例，即边缘概率
R可以用函数prop.table(x,margin) 计算这些比例，其命令是prop.table(x,margin)
当margin=1时，表示各个数据占行汇总数的比例
当margin=2表示各个数据占列汇总数的比例，省略时，表示占总和的比例

dw=table(smoke,study)
prop.table(dw,1) 

这里可以首先定义一个概率函数， 然后用apply()函数求边缘概率。

prop=function(x) x/sum(x)
apply(dw,2,prop) 

按行计算的边缘概率，不能直接应用apply(tab,1,prop)，而是要进行转置。

t(apply(dw,1,prop))

分类对分类–复式条形图

多变量分析中经常用到复式条形图
复式条形图是指由两个或两个以上小直条构成的条形图，与简单条形图相比，复式条形图多了一个分组因素，常用于考察比较两组研究对象的某观察指标。
R软件中作复式条形图的函数是barplot()。但是，作复式条形图之前应先对数值数据进行分组， 需要用table()函数作频数表。

例题1：
我们以上面的分类数据为例作条形图，粗略分析变量的分布情况。

par(mfrow=c(1,3))#设置图形窗口以一行三列形式输出
barplot(table(smoke, study))#以study为分类变量作条形图
barplot(table(study,smoke))#以smoke为分类变量作条形图
barplot(table(study,smoke),beside=T,legend.text=c("<5h","5~10h", ">10h"))#设置图例

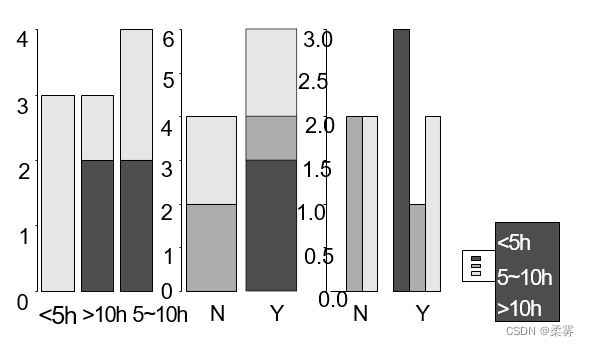
参数beside设置为False时，作出的图是分段式条形图，为True时作出的条形图是并列式，R默认的是False。

分类对数值–并列箱线图

示例如下：
有一个药物临床试验，得到实验组和对照组两组数据。
实验组：5,5,5,1,3,7,11,11,9,8
对照组：11,8,4,5,9,5,10,5,4,10

x=c(5,5,5,1,3,7,11,11,9,8)
y=c(11,8,4,5,9,5,10,5,4,10)
boxplot(x,y) #把x和y的箱线图画在一起

x变量的均值要小于y的均值，x、y变量都是偏态分布，x变量左偏，y变量右偏。

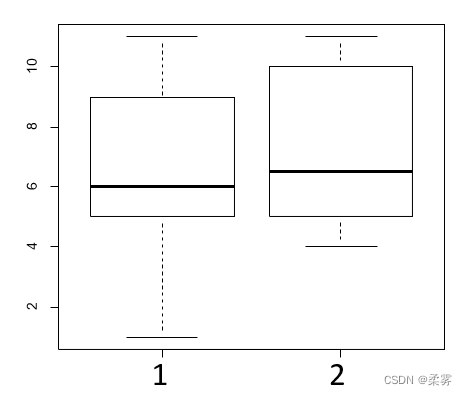
还可以把试用前和试用后的数据放在一组，另设一个虚拟变量，比如记实验组为1，对照组为2。

d=c(5,5,5,1,3,7,11,11,9,8, 11,8,4,5,9,5,10,5,4,10)
g=c(1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2)
boxplot(d~g)

或者使用更简洁的程序

d=c(x,y)
g=c(rep(1,10),rep(2,10))      #等价g=c(1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2)
boxplot(d~g)

要注意的是d~ g，分类变量要在~后面。

数值型数据对数值型数据

比较两个数值变量的方法有很多，可以从不同角度去比较
比如对两个独立的数值变量，既可以比较它们的分布是否相同，也可以分析是否存在着某种相关关系、回归关系等。

散点图

散点图（scatterplot）可以展现和分析两个数值变量的关系，在R里使用plot()函数做散点图。
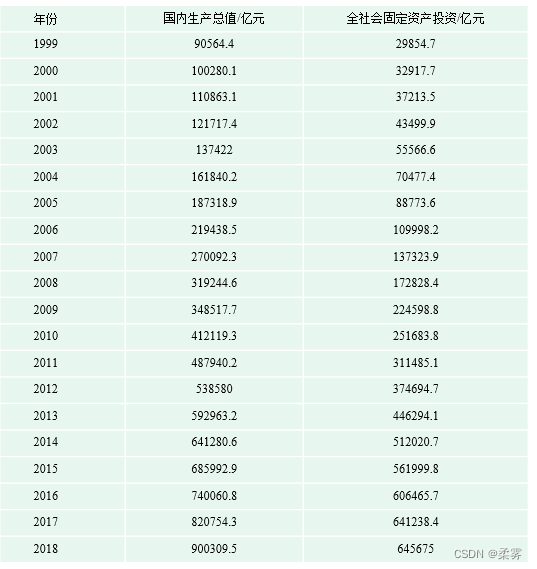
下面是从国家统计局网站收集1999-2018年我国国内生产总值（x）和全社会固定资产投资（y），绘制二者的散点图

gdp=c(90564.4,100280.1,110863.1,121717.4,137422,161840.2,187318.9,219438.5,270092.3,319244.6,348517.7,412119.3,487940.2,538580,592963.2,641280.6,685992.9,740060.8,820754.3,900309.5)
invest=c(29854.7,32917.7,37213.5,43499.9,55566.6,70477.4,88773.6,109998.2,137323.9,172828.4,224598.8,251683.8,311485.1,374694.7,446294.1,512020.7,561999.8,606465.7,641238.4,645675)

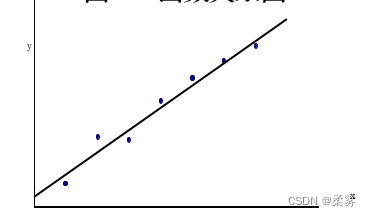
绘出两个变量的散点图

plot(gdp,invest) #作gdp,invest变量的散点图
abline(lm(invest~gdp)) #添加趋势线

可以看出，国民生产总值与全社会固定资产投资两者之间有比较强的线性关系，各个点大致分布在回归线的两边，具有比较强的线性关系。

相关系数

两个数值变量之间的关系大体可分为两类：
①确定性关系，研究是确定现象与非随机变量之间的关系， 例如，圆周长=2πr

②统计相关关系，研究非确定现象与随机变量之间的关系， 例如，家庭消费=f(收入，财富，年龄，消费观念)

对变量间统计依赖关系的考察主要是通过相关分析（ correlation analysis）或回归分析（regression analysis）来完成的。这里主要介绍相关分析。

Pearson相关系数(Pearson’s correlation coefficient)又叫相关系数或线性相关系数。它一般用字母r表示，其公式为:


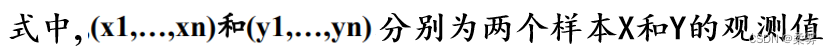
Pearson相关系数(Pearson’s correlation coefficient)又叫相关系数或线性相关系数。它一般用字母r表示，其公式为:

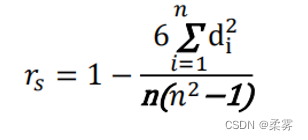
其中di = xi ? yi，xi和yi分别是两个变量按大小排位的等级，n是样本量。
Spearman相关系数取值在-1~1之间，与相关系数r有类似解释。

Kendallτ相关系数(Kendall’s τ) 是把所有的样本点配对，然后看每一对中的X和Y的观测值是否同时增加(或减少)
比如由点对(x1,y1)和(x2,y2)，可以算出乘积(x2-x1)(y2-y1) 是否大于0。如果大于0，则说明X和Y同时增长或同时下降，称这两点协同(concordant)，否则就是不协同
如果样本中协同的点数目多，则两个变量就更正相关一些；如果样本中不协同(discordant)的点数目多，两个变量就更负相关一些；如果既不正相关也不负相关，则为不相关。这里不用假设总体的分布，也可以检验。因此，这是一个非参数的度量。

Kendallτ也是在-1~1之间的数，也是越接近于1或-1就越相关，而接近0就不相关。
在R语言中求相关系数的函数是cor() 。 cor()函数默认求的是pearson相关系数。
在选项“method=”进行设置,可以求spearman 秩相关系数（ method=”spearman”） 和 Kendall τ相关系数（method=”kendall”）。

例题1：
求国民生产总值与全社会固定资产投资的相关系数。

cor(gdp,invest)  [1] 0.9931347
cor(invest,gdp)

[1] 0.9931347

结果说明：这两个变量具有非常高的线性相关程度，并且相关分析是不分自变量和因变量的
国民生产总值与全社会固定资产投资的相关系数等于全社会固定资产投资与国民生产总值的相关系数。

spearman秩相关系数如下

cor(gdp,invest, method="spearman")

[1] 1
spearman秩相关是一种秩相关，可先对数据求秩，然后再计算它们的pearson相关
下面用R编程计算spearman相关，R里的rank()函数提供了求秩功能。例如：

cor(rank(gdp),rank(invest))

[1] 1
结果说明，两个变量具有非常强的正等级相关
类似可以计算Kendall τ相关系数

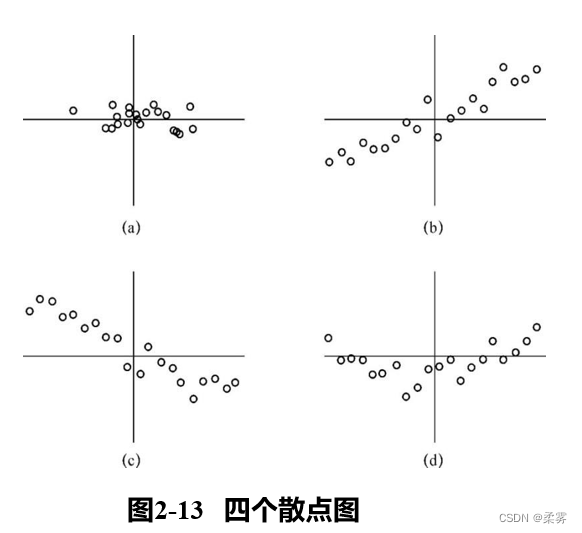
图2-13(a)看不出X和Y有任何关系，这些点完全是杂乱无章的,它们看上去是不相关的。
图2-13(b)显示当X增加时，Y大体上也增加,而且增加得较均匀，有大体上斜着递增直线那样的趋势。有这种关系的变量就称为(正)线性相关。
图2-13?和图2-13(b)类似，只不过有递减趋势，称为(负)线性相关。
图2-13(d)也表现出两个变量的很强的关系，但是不是线性的。

图2-13的四对变量的相关系数分别为-0.1395 , 0.9472 , -0.9393 , 0.3147
从相关系数上看，图(a)中 的变量存在低度相关;图(b)和图?分别表现高度正线性相关和高度负线性相关；图(d) 的变量肯定相关，但不是线 性相关，因此(线性)相关系数也很小。

---

练习

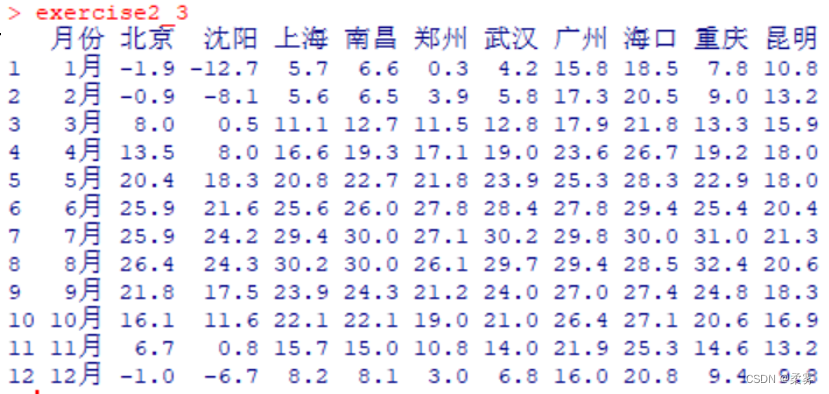
1、下面是我国十个城市2006年各月份气温数据（提供数据exercise2_3，不用自己录入）
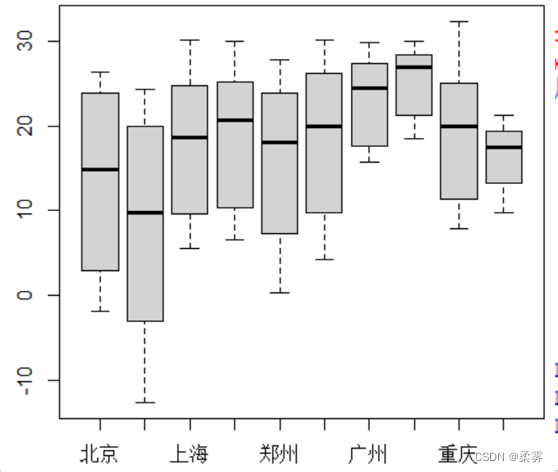
（1）按城市绘制箱线图，说明数据分布特点

load("C:ch2/exercise2_3.RData")
boxplot(exercise2_3[,-1])