回溯法求不等式的所有整数解

这份代码本来是用来解决这个问题的

但是，修改之后即可用来解决任意多个xi组成的满足不等式的整数解

这里用真代码而不是伪代码来表示

源代码：

#include<iostream>
using namespace std;
const int N=1010;
int p,q,r,goal,n;
int cnt,sum,MIN;
int A[N],t[N],s[5];
int Min(int a,int b,int c)
{
	int t=a<=b?a:b;
	return t<=c?t:c;
}
void solve(int k)
{	
	//i代表x取值 
	for(int i=0;i<=goal/MIN;i++)//注意i从0开始 
	{
		t[cnt++]=i;
		
//		int total=0;
//		for(int j=0;j<cnt;j++) total+=t[j];
		sum+=s[k]*i;
//		printf("solve(%d),i=%d,sum=%d\n",k,i,sum);
//		printf("几个系数为:");
//		for(int j=0;j<3;j++) printf("%d ",t[j]);
//		printf("\n");
		if(k!=n)
			solve(k+1);
		if(sum<=goal)
		{	
//			printf("----sum<=goal,solve(%d),i=%d,sum=%d,cnt=%d\n",k,i,sum,cnt);
			for(int j=0;j<3;j++) printf("%d ",t[j]);
			printf("\n");
		}
//		printf("solve(%d),i=%d,sum=%d,cnt=%d,执行完毕！\n",k,i,sum,cnt);

		cnt--;
		t[cnt]=0;
		sum-=s[k]*i;
		
		//如果i从1开始会导致缺解，只能获得以x1开头的各个解，
		//而不能获得以x2,x3开头的各个解如(0,3,0),(0,0,5) 
	}
}
int main()
{
	n=3;
	
	cin>>p>>q>>r>>goal;
	
	s[1]=p,s[2]=q,s[3]=r;
	
	MIN=Min(p,q,r);
	
	for(int i=1;i<=goal;i++) A[i]=i;
	
	solve(1);
	
	return 0;	
} 

运行结果：

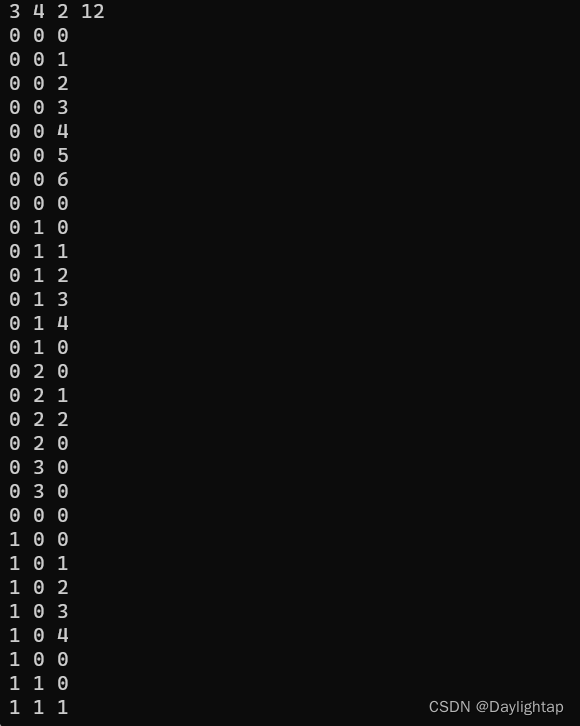
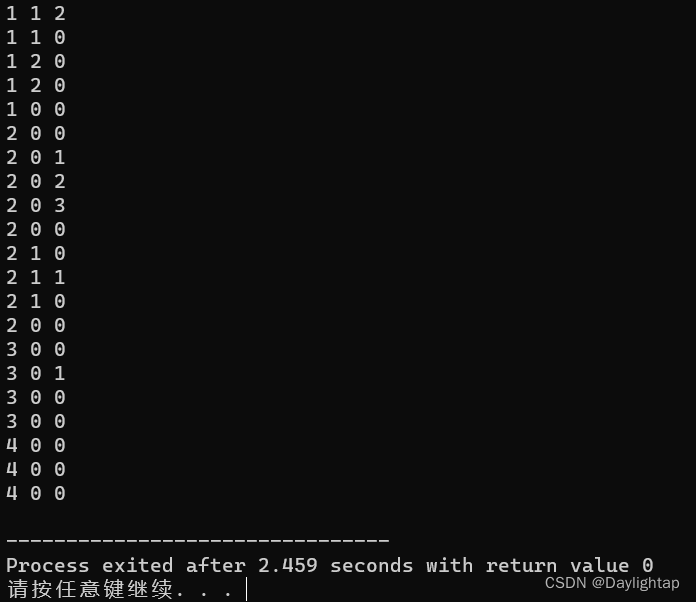
可以看到，这些解都是正确的。

现在做简单修改，把输入n和p,q,r的部分修改一下，即可用来解决任意多个自变量xi的不等式

（根据自变量个数修改N的值,如果自变量个数大于原来的N值1010）

注意修改之后s数组下标从1开始，因为这个下标和solve的递归层数（从第一层开始）相关联

	//n=3;
	
	//cin>>p>>q>>r>>goal;
	
	//s[1]=p,s[2]=q,s[3]=r;

    cin>>n>>goal;

    //注意这里下标从1开始，因为这个下标和solve的递归层数（从第一层开始）相关联
    for(int i=1;i<=n;i++) cin>>s[i];

最后，再把MIN函数修改一下即可