12.18拓扑排序,DAG,模板,课程安排
拓扑排序




有向无环图一定是拓扑序列,有向有环图一定不是拓扑序列。
无向图没有拓扑序列。
首先我们先来解释一下什么是有向无环图:
有向就是我们两个结点之间的边是有方向的,无环的意思就是整个序列中没有几个结点通过边形成一个圆环。
下图就是一个有向无环图,它也一定是拓扑序列。
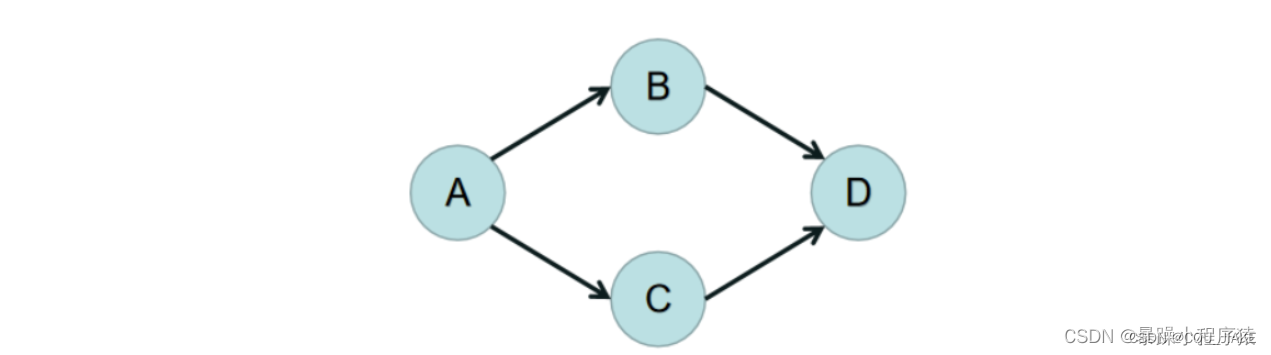
下图就是有向有环图:?

总结一下拓扑排序就是只有从前指向后的边,没有从后指向前的边。
(满足事件的先后顺序,类似于哈夫曼树的构建)
如果是一个有向无环图,那么一定有一个点的入度为0,如果找不到一个入度为0的点,这个图一定是带环的。
拓扑排序满足:每条边(x,y),x在序列中都在y前面。
拓扑排序的思路:
一个有向图,如果图中有入度为 0 的点,就把这个点删掉,同时也删掉这个点所连的边。
一直进行上面出处理,如果所有点都能被删掉,则这个图可以进行拓扑排序。
举例
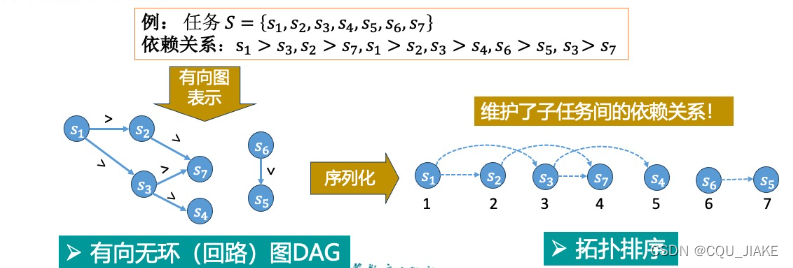

ABD
首先我们的有向无环图是这样的:
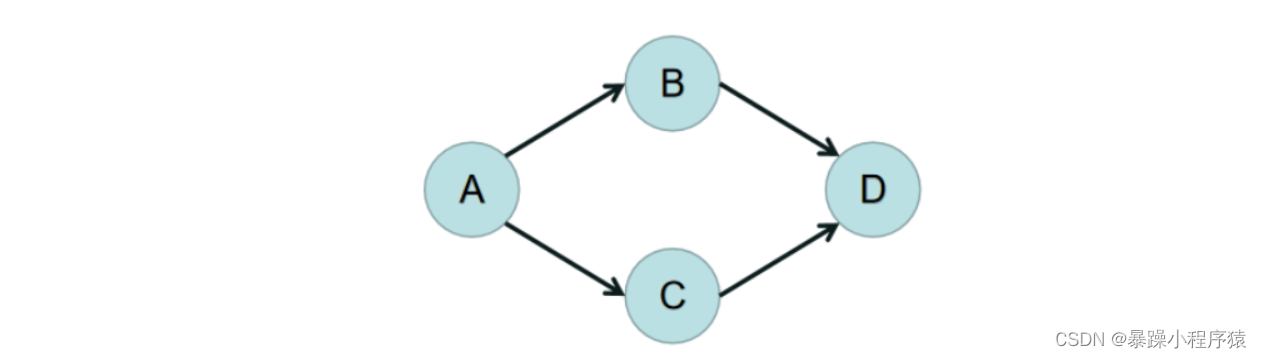
我们发现A的入度为0,那么A就可以作为源点(不会有边在它前面),然后删除A和A上所连的边,如下图:
然后我们发现B和C的入度都是0,那么同样删除B,C和B,C上所连的边,如下图:

然后D的入度为0,我们同样操作,最后图被删除干净,证明可以拓扑排序。
 ?
?
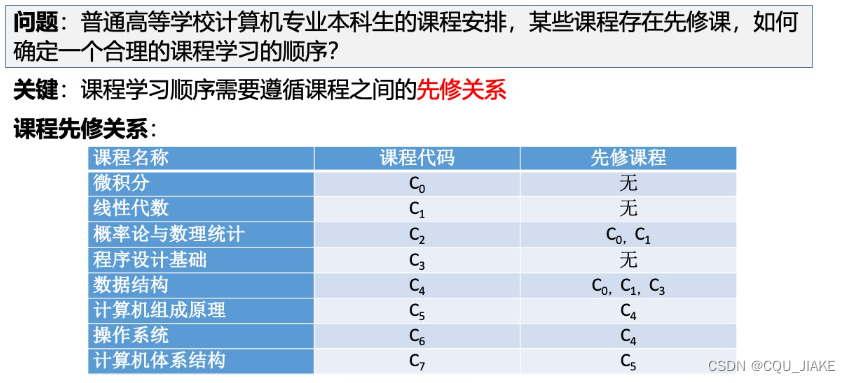
解题思路
首先记录各个点的入度
然后将入度为 0 的点放入队列
将队列里的点依次出队列,然后找出所有出队列这个点发出的边,删除边,同时边的另一侧的点的入度 -1。
如果所有点都进过队列,则可以拓扑排序,输出所有顶点。否则输出-1,代表不可以进行拓扑排序。
其他操作
计算入度

拓扑排序模板


在初始化的FOR循环中先遍历所有点,然后在WHILE中遍历所有边?
bool topsort()
{
int hh = 0, tt = -1;
// d[i] 存储点i的入度
for (int i = 1; i <= n; i++)
if (!d[i])
q[++tt] = i;
//先遍历d数组,然后把初始的d数组中所有入度为0的元素都加入到队列当中,I就是节点的编号
while (hh <= tt)
{
int t = q[hh++];//队列头节点
//H数组记录对应节点的第一条出边,Ne数组记录每条边的下一个索引
//h记录的是
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (--d[j] == 0)//先--,再判断是否为0
q[++tt] = j;
}
}
// 如果所有点都入队了,说明存在拓扑序列;否则不存在拓扑序列。
return tt == n - 1;//tt从-1开始,有n个节点时,最终停在n-1
}
//d数组记录的是目前每个节点的入度
//q数组记录的是待处理节点的编号,是源点
//h数组记录的是以下标为起点编号的第一条边
//ne数组记录的是同一起点下,每条出边所指向的下一条出边,它的下标标号就是边的标号
//e数组记录的是i边所指向的终点,下标为边的编号,记录的是边的终点时间复杂度
该代码的时间复杂度是O(V+E),其中V表示节点的数量,E表示边的数量。
在代码的第一个for循环中,遍历了所有的节点,所以时间复杂度是O(V)。
在代码的while循环中,每个节点的邻接链表中的每个边都会被访问一次。由于每个边会被访问一次且仅一次,所以总的边数是O(E)。因此,while循环的时间复杂度是O(E)。
综上所述,整个代码的时间复杂度是O(V+E)。这是因为该算法的主要操作是遍历节点和边,每个节点和每条边都只会被处理一次。所以,时间复杂度与节点数和边数成正比。
这样的复杂度意味着遍历所有的点和所有的边
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int h[N],e[N],ne[N],idx; //邻接表存储图
int n,m; //n个点,m个边
int q[N],d[N];//q表示队列,d表示点的入度
void add(int a,int b)
{
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
bool topsort()
{
int hh=0,tt=-1;
for(int i=1;i<=n;i++)
{
if(!d[i])//如果i这个点的入度为0,那么我们就入队
q[++tt]=i;
}
while(hh<=tt) //如果队列不为空
{
int t=q[hh++];//用t来接收队头的元素,同时队头指针hh++;
for(int i=h[t];i!=-1;i=ne[i])//我们来从t结点开始遍历它的边
{
int j=e[i];//t有一条边指向j
d[j]--;//删除掉t指向j的这条边,j的入度-1;
if(d[j]==0) //如果j的入度为0,那么我们就将j入队
q[++tt]=j;
}
}
return tt==n-1;
//表示如果n个点都入队了话,那么该图为拓扑图,返回true,否则返回false
//我们的tt初始值是-1,当插入一个值的时候tt先++在插入,所以我们一个有n个结点,全部入队的话tt指针应该是n-1;
}
int main()
{
cin>>n>>m;//保存点的个数和边的个数
memset(h,-1,sizeof(h));//初始化邻接表
for(int i=0;i<m;i++)//我们一共有m个边,所以我们循环插入边
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
d[b]++;//插入的边是由a指向b的,所以b的入度++;
}
if(topsort())
{
for(int i=0;i<n;i++)
printf("%d ",q[i]);
puts("");
}
else
puts("-1");
return 0;
}
例题


拓扑排序的特点是,根节点比孩子节点先访问。ACD,若采用后续遍历,即只要反转一次即可


本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【SpringBoot篇】基于Redis实现生成全局唯一ID的方法
- Java学习——Junit单元测试
- AI训练师常用的ChatGPT通用提示词模板
- 阿里云服务器固定带宽下载和上传速度对照表
- 实景无人直播——颠覆传统直播方式的创新尝试
- 【粉丝福利社】Flutter小白开发——跨平台客户端应用开发学习路线(文末送书-完结)
- Rust采集天气预报信息并实时更新数据
- 【libevent】IO引擎及实现
- el-form点击提交后把验证失败的数据传给了后端
- mmdetection训练自己的数据集