[Python] pytorch损失函数之MSELoss(均方误差损失)介绍和使用场景
发布时间:2024年01月06日
什么是MSE(均方误差)?
均方误差(Mean Squared Error,简称MSE)是用于衡量预测值与真实值之间差异的一种指标。它是实际观察值与预测值之差的平方和的平均值。
假设有n个样本,真实值分别为y?, y?, ……, y?,预测值分别为??, ??, ……, ??。
首先,我们可以定义误差(error)为预测值与真实值之间的差:
e? = y? - ??
则第i个样本的误差平方为:
e?2 = (y? - ??)2
我们希望得到所有样本误差平方的平均数,即均方误差。因此,我们可以计算所有样本误差平方的和,再除以样本数n:
MSE = (1/n) * Σ(y? - ??)2 (i=1,2,…,n)
?
均方误差越小,说明预测值与真实值越接近;均方误差越大,说明预测值与真实值之间的差异越大。
什么MSELoss(均方误差损失)?
MSELoss(均方误差损失)是PyTorch中用于计算预测值与真实值之间均方误差的损失函数。它主要用于回归问题,即预测连续值。
MESLoss使用案例
# 首先导入所需的库
import torch
import torch.nn as nn
# 创建MSELoss对象
mse_loss = nn.MSELoss()
# 定义预测值和真实值:
predictions = torch.randn(3, 5) # 随机生成一个3x5的张量作为预测值
targets = torch.randn(3, 5) # 随机生成一个3x5的张量作为真实值
print('predictions:', predictions)
print('targets:', targets)
# 计算MSELoss
loss = mse_loss(predictions, targets)
print(loss)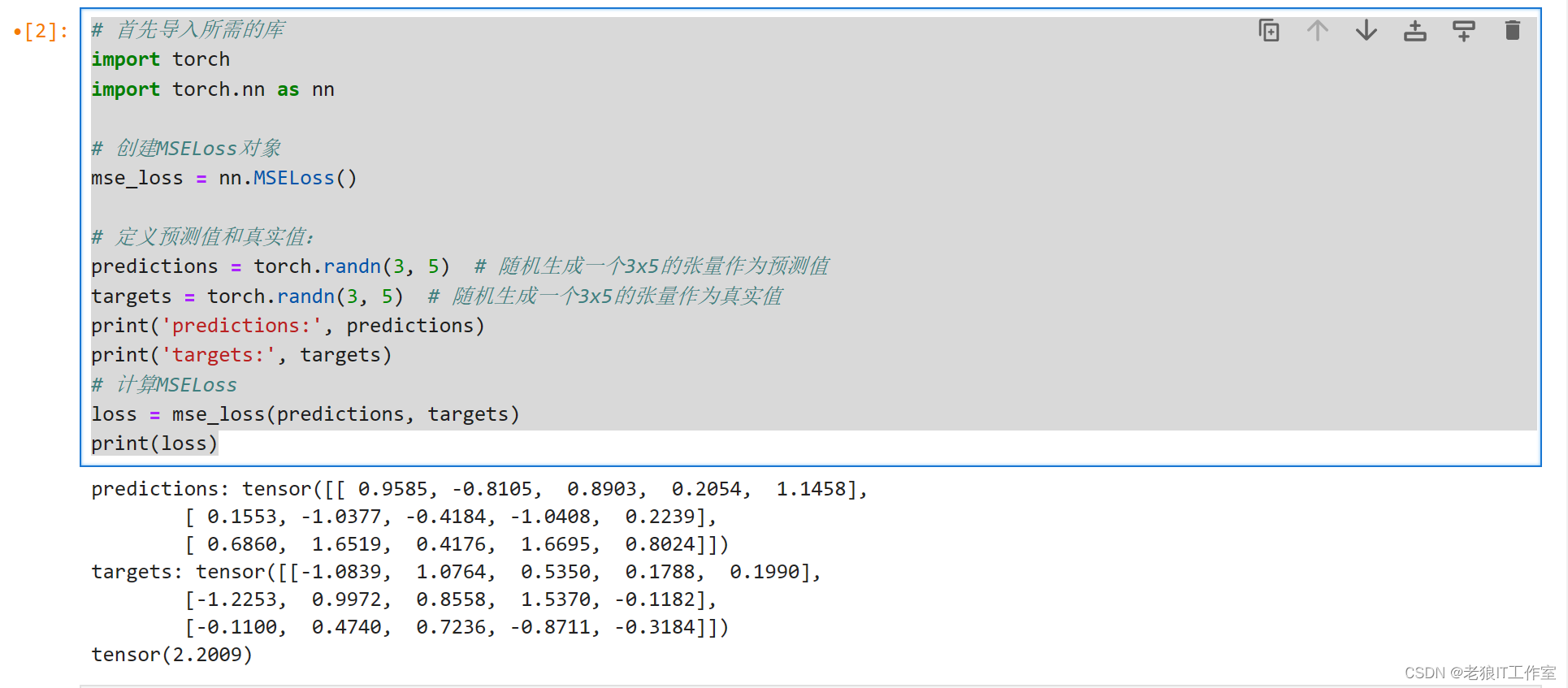
参考资料
文章来源:https://blog.csdn.net/u011775793/article/details/135411892
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 竞赛练一练 第23期:NOC大赛每日一练,python题目刷题第8天,包含答案解析
- 【为什么重写equals 还要重写hashcode?】
- 【每日一题】2397. 被列覆盖的最多行数-2024.1.4
- [C#]Onnxruntime部署Chinese CLIP实现以文搜图以文找图功能
- openwrt docker nginx 站点搭建
- 机器学习扩散模型简介
- vue3-回顾之,状态管理神器 大菠萝- pinia
- 【Spring连载】使用Spring访问 Apache Kafka(四)----监听器容器属性
- cnPuTTY 0.80.0.1—PuTTY Release 0.80中文版本简单说明~~
- 在Centos7中:通过Docker安装MySQL5.7(保姆级)