牛客竞赛算法入门题单打卡 K Number

链接：登录—专业IT笔试面试备考平台_牛客网
来源：牛客网
?

题目描述

We define Shuaishuai-Number as a number which is?the sum of a prime square(平方), prime cube(立方), and prime fourth power(四次方).

The first four Shuaishuai numbers are:

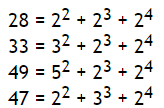
How many Shuaishuai numbers in [1,n]? (1<=n<=50 000 000)

输入描述:

The input will consist of a integer n.

输出描述:

You should output how many Shuaishuai numbers in [1...n]

示例1

输入

复制28

28

输出

复制1

1

说明

There is only one Shuaishuai number

思路

先欧拉筛筛出所有的素数，再暴力枚举

注意点

这里存储数据用set，因为set中每个数据只会出现一次

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int isprime[N],prime[N];//是否是素数，当前筛出的素数
int cnt=0;//当前筛出的素数个数
void euler(int n)
{
	memset(isprime,0,sizeof(isprime));//0表示是素数，1不是
	isprime[1]=1;
	for(int i=2;i<7800;i++)
	{
		if(!isprime[i])
		{
			prime[cnt++]=i;
		}
		for(int j=0;j<cnt&&i*prime[j]<7800;j++)
		{
			isprime[i*prime[j]]=1;
			if(i%prime[j]==0)break;
		}
	}
}
int main()
{
	long long n;
	cin>>n;
	euler(n);
	set<long long>s;
	for(int i=0;i<cnt;i++)
		for(int j=0;j<cnt;j++)
			for(int k=0;k<cnt;k++)
			{
				if(pow(prime[i],2)+pow(prime[j],3)+pow(prime[k],4)<=n)
				{
					s.insert(pow(prime[i],2)+pow(prime[j],3)+pow(prime[k],4));
				}
				else break;
			}
	cout<<s.size();
}