四种无监督聚类算法说明
目录
?一、K-Means无监督学习(K-Means)的认识-CSDN博客??????
?二、Mini-Batch K-Means -- Centroid models
?三、AffinityPropagation (Hierarchical) -- Connectivity models
四、Mean Shift -- Centroid models
无监督聚类是一种机器学习技术,用于将数据分组成不同的类别,而无需提前标记或指导。在无监督聚类中,算法通过分析数据之间的相似性和差异性,自动将数据划分为具有相似特征的组。?
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn.cluster as cluster
import time
%matplotlib inline
data = np.load('clusterable_data.npy')#这是一个类似细胞的数据集
plt.scatter(data.T[0], data.T[1], c='b')
frame = plt.gca()
frame.axes.get_xaxis().set_visible(False)
frame.axes.get_yaxis().set_visible(False)?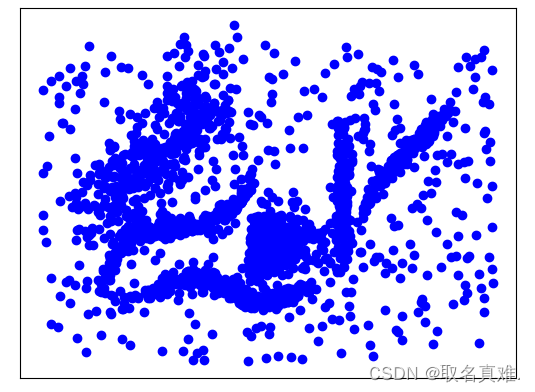
?一、K-Means无监督学习(K-Means)的认识-CSDN博客??????
#K-Means --Centroid models
# k-means clustering
from numpy import unique
from sklearn.cluster import KMeans
from matplotlib import pyplot
# define the model
model = KMeans(n_clusters=6)
# fit the model
model.fit(data)
# assign a cluster to each example
yhat = model.predict(data)
# retrieve unique clusters
clusters = unique(yhat)
palette = sns.color_palette('deep', np.unique(yhat).max() + 1)
colors = [palette[x] if x >= 0 else (0.0, 0.0, 0.0) for x in yhat]
plt.scatter(data.T[0], data.T[1], c=colors)
frame = plt.gca()
frame.axes.get_xaxis().set_visible(False)
frame.axes.get_yaxis().set_visible(False)
plt.title('Clusters found by K-Means')
?二、Mini-Batch K-Means -- Centroid models
Mini-Batch K-Means是一种改进的K-Means聚类算法,它使用了一种随机化的方法来提高运行效率。Centroid models是指聚类过程中使用的中心模型,用于代表每个簇的质心。
在传统的K-Means算法中,聚类过程涉及计算每个数据点与所有质心之间的距离,并将数据点分配到距离最近的质心所代表的簇中。然后,通过计算每个簇中数据点的平均值,更新每个簇的质心。
而在Mini-Batch K-Means中,为了提高计算效率,在每次迭代时只选取部分数据点进行计算。具体做法是,每次从数据集中随机选择一小部分数据(称为Mini-Batch),然后计算这些数据点与当前质心之间的距离,将它们分配到距离最近的簇中,并更新这些簇的质心。
Centroid models在Mini-Batch K-Means中起到了表示每个簇的作用。它们是每个簇的质心,代表了该簇中所有数据点的平均值。在每次迭代中,通过对Mini-Batch中的数据点进行聚类,更新质心,从而不断优化簇的分布和数据点的分配。
通过使用Mini-Batch K-Means和Centroid models,可以加速聚类过程并处理大规模的数据集,同时保持较高的聚类质量。
# mini-batch k-means clustering
from numpy import unique
from sklearn.cluster import MiniBatchKMeans
from matplotlib import pyplot
model = MiniBatchKMeans(n_clusters=6)
# fit the model
model.fit(data)
# assign a cluster to each example
yhat = model.predict(data)
# retrieve unique clusters
clusters = unique(yhat)
palette = sns.color_palette('deep', np.unique(yhat).max() + 1)
colors = [palette[x] if x >= 0 else (0.0, 0.0, 0.0) for x in yhat]
plt.scatter(data.T[0], data.T[1], c=colors)
frame = plt.gca()
frame.axes.get_xaxis().set_visible(False)
frame.axes.get_yaxis().set_visible(False)
plt.title('Clusters found by Mini-Batch K-Means')?
?三、AffinityPropagation (Hierarchical) -- Connectivity models
AffinityPropagation是一种基于图论的聚类算法,它可以自动确定每个样本的聚类中心。它通过计算样本之间的相似性来构建一个图模型,并在图上进行迭代更新以确定聚类中心。
在AffinityPropagation算法中,样本之间的相似性通过计算欧氏距离、相关系数或其他相似性度量得到。根据相似性度量,构建一个相似度矩阵。然后,算法通过迭代更新样本之间的消息传递来确定每个样本的聚类中心。
具体来说,AffinityPropagation算法通过以下步骤进行聚类:
初始化相似度矩阵,将样本之间的相似性度量填入矩阵中。
在相似度矩阵上进行迭代更新,直到满足停止准则。每一轮更新包括两个步骤:
- 确定每个样本的"责任"(responsibility)值,表示该样本选择其他样本作为聚类中心的程度。
- 确定每个样本的"可用性"(availability)值,表示其他样本选择该样本作为聚类中心的程度。
根据最终的聚类中心确定样本的聚类归属。
AffinityPropagation算法的主要优点是不需要预先指定聚类数量,能够自动确定每个样本的聚类中心。然而,它的计算复杂度较高,并且对初始参数的选择敏感。此外,它的结果可能会受到相似性度量的选择和参数调整的影响。
from sklearn.cluster import AffinityPropagation
from matplotlib import pyplot
from numpy import unique
# fit the model
model = AffinityPropagation(damping=0.95)
model.fit(data)
yhat = model.predict(data)
# retrieve unique clusters
clusters = unique(yhat)
palette = sns.color_palette('deep', np.unique(yhat).max() + 1)
colors = [palette[x] if x >= 0 else (0.0, 0.0, 0.0) for x in yhat]
plt.scatter(data.T[0], data.T[1], c=colors)
frame = plt.gca()
frame.axes.get_xaxis().set_visible(False)
frame.axes.get_yaxis().set_visible(False)
plt.title('Clusters found by AffinityPropagation')#显然这种方法不适合于用在类似细胞结构的数据上
clusters
'''结果:array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41], dtype=int64)'''
四、Mean Shift -- Centroid models
Mean Shift是一种基于密度的非参数化聚类算法。它的目标是发现数据分布中的概率密度最大值,从而确定聚类中心。该算法通过不断地迭代更新数据点的位置,使其向概率密度较高的区域移动,直到达到局部最大值。
具体来说,Mean Shift算法首先选择一个初始点作为聚类中心,然后计算该点周围数据点的平均位置(即mean shift)。然后将该平均位置作为新的聚类中心,并重复该过程,直到聚类中心不再发生明显的变化或达到设定的迭代次数。
在算法的最终阶段,可以根据聚类中心的邻域关系将数据点分配到不同的聚类。Mean Shift算法的优点是不需要预先指定聚类数量,可以自动适应数据的分布形态。然而,它在处理高维数据时可能会受到维数灾难的影响,并且对初始中心点的选择较为敏感。因此,在实际应用中,可能需要进行参数调优或配合其他算法来提高聚类效果。
# mean shift clustering
from numpy import unique
from sklearn.cluster import MeanShift
from matplotlib import pyplot
# define the model
model = MeanShift(bandwidth=0.175,cluster_all=False)
# fit model and predict clusters
yhat = model.fit_predict(data)
# retrieve unique clusters
clusters = unique(yhat)
palette = sns.color_palette('deep', np.unique(yhat).max() + 1)
colors = [palette[x] if x >= 0 else (0.0, 0.0, 0.0) for x in yhat]
plt.scatter(data.T[0], data.T[1], c=colors)
frame = plt.gca()
frame.axes.get_xaxis().set_visible(False)
frame.axes.get_yaxis().set_visible(False)
plt.title('Clusters found by Mean Shift')
clusters
#结果:array([-1, 0, 1, 2, 3, 4])
#-1表示噪音,不属于某个群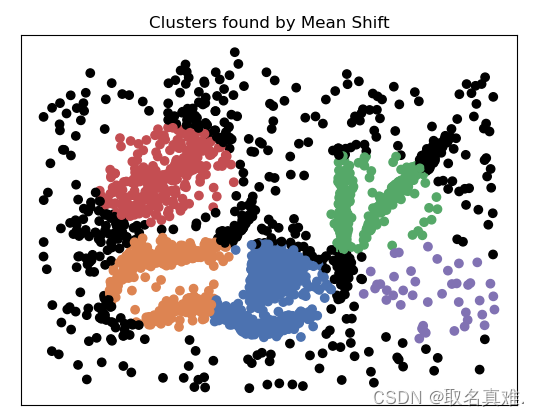
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- vue:this.reload()跟this.$router.replace的区别
- 【前后端的那些事】解放前端!10min快速上手人人代码生成器(前端篇)
- VS Code+MinGW 搭建Windows C++开发环境
- 【java问题解决】-word转pdf踩坑
- 探索Web开发的未来——使用KendoReact服务器组件
- 解决Android AAPT: error: resource android:attr/lStar not found. 问题
- uniapp中复选框的使用
- STM32 CubeMX 中断NVIC 实战 (超详细配30张高清图,附源码)
- halcon字符检测
- WT588F02B-8S语音芯片:灵活应用的语音播放利器,实现多重优势