刷题04 字符串mid

记录一些和字符数组有关的题目

之前代码随想录day08里面有一些涉及翻转字符串的操作可以一起回顾。

8.字符串转换整数（atoi）

? ? ? ? 除了单纯的转换之外还涉及到去空格，判断正负，以及判断是否溢出的操作。

 int myAtoi(char* s) {
    int i=0;
    bool flag=0;
    int n=strlen(s);
    //对空格进行操作
    while(i<n&&s[i]==' ') i++;
    if(i<n&&s[i]=='-'){
        //负数
        flag=1;
        i++;
    }else if(i<n&&s[i]=='+'){
        //正数
        flag=0;
        i++;
    }
    int sum=0;
    for(;i<strlen(s);++i){
        if(s[i]>='0'&&s[i]<='9'){
            //判断是否溢出，溢出就返回最大或者最小值
            if (sum>(INT_MAX-(s[i]-'0'))/10) {
                return flag==0? INT_MAX : INT_MIN;
            }
            sum=sum*10+(s[i]-'0');
        }else{
            //一旦碰到不是数字的值直接跳出循环
            break;
        } 
    }
    if(flag) return -sum;
    return sum;
}

670.最大交换

????????这题最开始想错了，还以为是找到最大的字符和第一个字符交换就完事了，但是如果第一个字符已经最大则需要把次大的字符交换到第二位，以此类推。这道题主要是要注意字符数组的各种操作一定要非常熟练。

? ? ? ? 错误代码：

????????用到了整数转字符数组，字符数组转整数的很原始的操作，可以用sprintf与atoi进行代替。

int maximumSwap(int num) {
    char str[10];
    int len=0;
    int temp=num;
    while(temp){
        int cur=temp%10;
        char s=cur+'0';
        str[len++]=s;
        temp/=10;
    }
    str[len]='\0';
    //找最大的那个数
    char mm=str[0];
    int index=0;
    for(int i=0;i<len;++i){
        if(str[i]>mm){
            index=i;
        }
    }
    //跟头一个数交交换
    char t=str[len-1];
    str[len-1]=str[index];
    str[index]=t;
    //字符数组化为数字
    int ans=0;
    for(int i=len-1;i>=0;--i){
        ans=ans*10+str[i]-'0';
    }
    return ans;
}

? ? ? ? 正确解法：暴力解

void swap(char* s1,char* s2){
    char temp=*s1;
    *s1=*s2;
    *s2=temp;
}
int maximumSwap(int num) {
    char str[100];
    sprintf(str,"%d",num);
    int n=strlen(str);
    int mmax=num;
    for(int i=0;i<n;++i){
        for(int j=i+1;j<n;++j){
            swap(&str[i],&str[j]);
            mmax=fmax(mmax,atoi(str));//更新最大值
            swap(&str[i],&str[j]);//恢复
        }
    }
    return mmax;
}

? ? ? ? 贪心算法：

????????每一位数字应该不小于所有排它后面的数字，否则找最大的且排最后面的数字与之交换

void swap(char* s1,char* s2){
    char temp=*s1;
    *s1=*s2;
    *s2=temp;
}
int maximumSwap(int num) {
    char str[100];
    sprintf(str,"%d",num);
    int n=strlen(str);
    int maxIdx=n-1;
    int idx1=-1,idx2=-1;
    for(int i=n-1;i>=0;--i){
        if(str[i]>str[maxIdx]){
            maxIdx=i;
        }else if(str[i]<str[maxIdx]){
            idx1=i;
            idx2=maxIdx;
        }
    }
    if(idx1>=0){
        swap(&str[idx1],&str[idx2]);
        return atoi(str);
    }else{
        return num;
    }
}

?179.最大数

给定一组非负整数?nums，重新排列每个数的顺序（每个数不可拆分）使之组成一个最大的整数。

注意：输出结果可能非常大，所以你需要返回一个字符串而不是整数。

示例 1：

输入：nums = [10,2]
输出："210"

? ? ? ? ?此题重要的一点是如何写比较函数，要将两个数字拼接到一起进行比较，因此要确定放在后面的数字的位数，让方前面的数字去乘相应的位数的值，大的那个数要放在前面，就是y x大就把y放在x的前面，相当于y<x

unsigned long long cmp(int* x,int* y){
    unsigned long long sx=10,sy=10;
    while(sx<=*x){
        sx*=10;
    }
    while(sy<=*y){
        sy*=10;
    }
    return sx*(*y)+(*x)-sy*(*x)-(*y);//会溢出
}
char* largestNumber(int* nums, int numsSize) {
    qsort(nums,numsSize,sizeof(int),cmp);
    if(nums[0]==0){
        char *ret=malloc(sizeof(char)*2);
        ret[0]='0',ret[1]='\0';
        return ret;
    }
    char *ret=malloc(sizeof(char)*1000);
    char *p=ret;
    for(int i=0;i<numsSize;++i){
        sprintf(p,"%d",nums[i]);
        p+=strlen(p);
    }
    return ret;
}

402.移除k位数字

给你一个以字符串表示的非负整数?num?和一个整数?k?，移除这个数中的?k?位数字，使得剩下的数字最小。请你以字符串形式返回这个最小的数字。

示例 1 ：

输入：num = "1432219", k = 3
输出："1219"
解释：移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219 。

? ? ? ? 从0到n-1进行遍历，如果下一个数字小就替换，大就保留当前值。

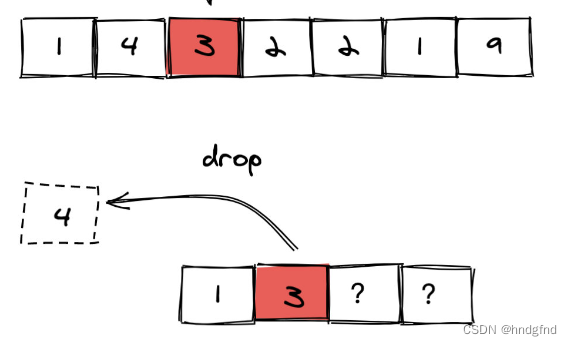
? ? ? ? 同一个单调栈存能够留下的元素，每次判断栈顶的元素能否留下。?

class Solution {
public:
    string removeKdigits(string num, int k) {
        vector<char> stk;
        for (auto& digit: num) {
            while (stk.size() > 0 && stk.back() > digit && k) {
                //栈不为空，栈顶元素比当前值大时，需要替换
                stk.pop_back();
                k -= 1;
            }
            stk.push_back(digit);
        }
        //如果k不为0时，将栈顶元素都弹出
        for (; k > 0; --k) {
            stk.pop_back();
        }

        string ans = "";
        bool isLeadingZero = true;
        for (auto& digit: stk) {
            //去掉前面的0
            if (isLeadingZero && digit == '0') {
                continue;
            }
            isLeadingZero = false;
            ans += digit;
        }
        return ans == "" ? "0" : ans;
    }
};

318.最大单词长度的乘积

给你一个字符串数组?words?，找出并返回?length(words[i]) * length(words[j])?的最大值，并且这两个单词不含有公共字母。如果不存在这样的两个单词，返回?0?。

示例?1：

输入：words = ["abcw","baz","foo","bar","xtfn","abcdef"]
输出：16 
解释：这两个单词为 "abcw", "xtfn"

? ? ? ? 此题关键在于怎样判断两个字符串没有公共字符，而这里使用的是位运算。?

int maxProduct(char ** words, int wordsSize){
    int makes[wordsSize];
    for(int i=0;i<wordsSize;++i){
        makes[i]=0;
        for(int j=0;j<strlen(words[i]);++j){
            makes[i]|=1<<(words[i][j]-'a');//记录第i-1个字符串的字符
        }
    }
    int ans=0;
    for(int i=0;i<wordsSize;++i){
        for(int j=i+1;j<wordsSize;++j){
            if((makes[i]&makes[j])==0){//如果没有重复的字符
                int cur=strlen(words[i])*strlen(words[j]);
                if(cur>ans){
                    ans=cur;
                }
            }
        }
    }
    return ans;
}

1143.最长公共子序列

????????给定两个字符串?text1?和?text2，返回这两个字符串的最长?公共子序列?的长度。如果不存在?公共子序列?，返回?0?。

????????一个字符串的?子序列?是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，"ace"?是?"abcde"?的子序列，但?"aec"?不是?"abcde"?的子序列。

两个字符串的?公共子序列?是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

? ? ? ? 二维数组动态规划，其中 dp[i][j] 表示 text1[0:i]、text2[0:j]的最长公共子序列的长度。注意初始化数组用函数memset（dp，0，sizeof(dp)）

int longestCommonSubsequence(char* text1, char* text2) {
    int m=strlen(text1),n=strlen(text2);
    int dp[m+1][n+1];
    memset(dp,0,sizeof(dp));
    for(int i=1;i<=m;++i){
        char c1=text1[i-1];
        for(int j=1;j<=n;++j){
            char c2=text2[j-1];
            if(c1==c2){
                dp[i][j]=dp[i-1][j-1]+1;
            }else{
                dp[i][j]=fmax(dp[i-1][j],dp[i][j-1]);
            }
        }
    }
    return dp[m][n];
}

647.回文子串

? ? ? ? 计算回文子串的个数。

? ? ? ? ?枚举回文串的中心，中心可能是一个，也可能是两个，然后从中心向两边拓展，如果不相等就退出循环。

int countSubstrings(char* s) {
    int n=strlen(s),ans=0;
    //枚举回文串的中心
    for(int i=0;i<n;++i){
        for(int j=0;j<=1;++j){
            //j=0,中心是一个点，j=1,中心是两个点
            int l=i;
            int r=i+j;
            while(l>=0&&r<n&&s[l--]==s[r++]){
                ans++;
            }
        }
    }
    return ans;
}

5.最长回文子串

?给你一个字符串?s，找到?s?中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

? ? ? ? ? ? 第一次不通过是因为误认为只要i从前往后遍历，j从后往前遍历，就可以发现最长的子串，但是一个break只能跳出一层循环，因此还会继续遍历，因此还需要记录最大长度，只有大于这个最大长度时才会更新左右下标。

bool isvaild(char *s,int l,int r){
    while(l<r){
        if(s[l]!=s[r]){
            return false;
        }
        l++;
        r--;
    }
    return true;
}
char* longestPalindrome(char* s) {
    int n=strlen(s);
    if(n<2) return s;
    int left=0,right=0;
    int mmax=0;
    for(int i=0;i<n;++i){
        for(int j=n-1;j>i;--j){
            if(isvaild(s,i,j)&&(j-i+1)>mmax){
                left=i;
                right=j;
                mmax=j-i+1;
                break;
            }
        }
    }
    char* ans=malloc(sizeof(char)*(n+1));
    int t=0;
    for(int i=left;i<=right;++i){
        ans[t++]=s[i];
    }
    ans[t]='\0';
    return ans;
}

97.交错字符串?

?给定三个字符串?s1、s2、s3，请你帮忙验证?s3?是否是由?s1?和?s2?交错?组成的。

两个字符串?s?和?t?交错?的定义与过程如下，其中每个字符串都会被分割成若干?非空?子字符串：

• s = s1 + s2 + ... + sn
• t = t1 + t2 + ... + tm
• |n - m| <= 1
• 交错?是?s1 + t1 + s2 + t2 + s3 + t3 + ...?或者?t1 + s1 + t2 + s2 + t3 + s3 + ...

注意：a + b?意味着字符串?a?和?b?连接。

? ? ? ? 动态规划：dp(i,j) 表示s1的前i个元素和 s2的前j个元素是否能交错组成 s3的前i+j个元素,

bool isInterleave(char* s1, char* s2, char* s3) {
    int n=strlen(s1),m=strlen(s2),t=strlen(s3);
    int dp[n+1][m+1];
    //dp(i,j) 表示s1的前i个元素和 s2的前j个元素是否能交错组成 s3的前i+j个元素
    memset(dp,0,sizeof(dp));
    if(n+m!=t) return false;
    dp[0][0]=true;
    for(int i=0;i<=n;++i){
        for(int j=0;j<=m;++j){
            int p=i+j-1;
            if(i>0){
                dp[i][j]|=(dp[i-1][j]&&s1[i-1]==s3[p]);
            }
            if(j>0){
                dp[i][j]|=(dp[i][j-1]&&s2[j-1]==s3[p]);
            }
        }
    }
    return dp[n][m];
}

151.反转字符串中的单词?

给你一个字符串?s?，请你反转字符串中?单词?的顺序。

单词?是由非空格字符组成的字符串。s?中使用至少一个空格将字符串中的?单词?分隔开。

返回?单词?顺序颠倒且?单词?之间用单个空格连接的结果字符串。

注意：输入字符串?s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中，单词间应当仅用单个空格分隔，且不包含任何额外的空格。

示例 1：

输入：s = "the sky is blue"
输出："blue is sky the

? ? ? ? 翻转字符串，还有去除多余空格的操作。?

//翻转字符串
void reverse(char *s,int left,int right){
    int i=left,j=right-1;
    while(i<j){
        char temp=s[i];
        s[i]=s[j];
        s[j]=temp;
        i++;j--;
    }
}
//除去单词两端的空格
void removeExtraSpace(char* s) {
    int start = 0; 
    int end = strlen(s) - 1; 
    while (s[start] == ' ') start++; //找到第一个非空格字符
    while (s[end] == ' ') end--; // 找到第一个非空格字符
    int slow = 0; // 指向新字符串的下一个写入位置的指针
    for (int i = start; i <= end; i++) { 
        if (s[i] == ' ' && s[i+1] == ' ')  { // 如果当前字符是空格，并且下一个字符也是空格，则跳过
            continue;
        }
        s[slow] = s[i]; // 否则，将当前字符复制到新字符串的 slow 位置
        slow++;
    }
    s[slow] = '\0'; // 在新字符串的末尾添加一个空字符
}
char* reverseWords(char* s) {
    removeExtraSpace(s);
    int n=strlen(s);
    reverse(s,0,n);//翻转整个字符串
    int slow=0;
    for(int i=0;i<=n;++i){
        if(s[i]==' '||s[i]=='\0'){//一个单词结束
            reverse(s,slow,i);
            slow=i+1;//指向下一个单词
        }
    }
    return s;
}

557.反转字符串中的单词 III

给定一个字符串?s?，你需要反转字符串中每个单词的字符顺序，同时仍保留空格和单词的初始顺序。

示例 1：

输入：s = "Let's take LeetCode contest"
输出："s'teL ekat edoCteeL tsetnoc"?

void swap(char *a,char *b){
    char temp=*a;
    *a=*b;
    *b=temp;
    return;
}
char* reverseWords(char* s) {
    int n=strlen(s);
    int i=0;
    while(i<n){
        int l=i;
        //确定单词首尾
        while(i<n&&s[i]!=' '){
            i++;
        }
        int r=i-1;
        //翻转
        while(l<r){
            swap(s+l,s+r);
            l++;r--;
        }
        //去空格
        while(i<n&&s[i]==' '){
            i++;
        }
    }
    return s;
}

402.移除K位数字

给你一个以字符串表示的非负整数?num?和一个整数?k?，移除这个数中的?k?位数字，使得剩下的数字最小。请你以字符串形式返回这个最小的数字。

示例 1 ：

输入：num = "1432219", k = 3
输出："1219"
解释：移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219 。

? ? ? ? 单调栈的思想，用一个数组模拟栈，且栈中元素始终保持单调。遍历数组，如果下一个元素大于前一个元素，直接存入数组，如果下一个元素小于栈顶元素，将刚刚存入的数依次弹出，k--，然后继续进行判断，如果最后k不为0，则将栈顶的元素弹出。

?

char * removeKdigits(char * num, int k){
    int n=strlen(num);
    int top=0;//top指向当前的栈顶
    char* stk=malloc(sizeof(char)*(n+1));
    stk[0]=num[0];
    for(int i=1;i<n;++i){
        while(top>=0&&stk[top]>num[i]&&k>0){
            top--;
            k--;
        }
        stk[++top]=num[i];
    }
    //k不为0时弹出栈顶
    top-=k;
    char* ans=malloc(sizeof(char)*(n+1));
    int anssize=0;
    bool isZore=true;
    //将开头的0去除
    for(int i=0;i<=top;++i){
        if(isZore&&stk[i]=='0'){
            continue;
        }
        isZore=false;
        ans[anssize++]=stk[i];
    }
    //判断是否为0
    if(anssize==0){
        ans[0]='0';ans[1] ='\0';
    }else{
        ans[anssize]='\0';
    }
    return ans;
}

415.字符串相加

给定两个字符串形式的非负整数?num1?和num2?，计算它们的和并同样以字符串形式返回。

你不能使用任何內建的用于处理大整数的库（比如?BigInteger），?也不能直接将输入的字符串转换为整数形式。

示例 1：

输入：num1 = "11", num2 = "123"
输出："134"

char * addStrings(char * num1, char * num2){
    int i=strlen(num1)-1,j=strlen(num2)-1;
    char* ans=malloc(sizeof(char)*(i+j+3));
    int ll=0;
    int carry=0;
    while(i>=0||j>=0){
        int x=i>=0?num1[i]-'0':0;
        int y=j>=0?num2[j]-'0':0;
        int sum=x+y+carry;
        carry=sum/10;
        sum=sum%10;
        ans[ll++]='0'+sum;
        i--;j--;
    }
    if(carry) ans[ll++]='1';
    ans[ll]='\0';
    int l=0,r=strlen(ans)-1;
    while(l<r){
        char t=ans[l];
        ans[l]=ans[r];
        ans[r]=t;
        l++;r--;
    }
    return ans;
}

459.重复的子字符串

?给定一个非空的字符串?s?，检查是否可以通过由它的一个子串重复多次构成。

bool repeatedSubstringPattern(char* s) {
    int n=strlen(s);
    int j=0;
    //枚举子串长度
    for(int i=1;i<n;++i){
        //判断是否总长度为子串的整数倍
        if(n%i==0){
            bool match=true;
            //依次向后遍历判断
            for(int j=i;j<n;++j){
                if(s[j]!=s[j-i]){
                    match=false;
                    break;
                }
            } 
            if(match) return true;
        }
        
    }
    return false;
}

?